아핀 변환

결론만 이야기하면 선형과 아핀변환은 같다 (선형변환 == 아핀변환)
보통 y=Ax 를 선형변환이라고 말하고 아핀 변환은 y=Ax + b (b는 변위, 위치벡터)로 표현하는데
그래픽스에서는 변위에 해당하는 b를 행렬 A에 포함시켜서 계산하기 때문에 둘이 서로 같다고 말할 수 있다고 한다.

기존 선형 변환의 개념은 벡터가 원점에서 출발하는 것으로 정의한다 (크기, 회전, 밀기)
(*그리고 벡터는 크기와 방향을 갖는다 위치라는 개념이 없다)
그래서 위치와 나머지 선형변환 사이에 연산을 하기위해 정의한 공간아 Affine space라고 한다.
그러니까 vector와 point를 같이 다루는 공간이 affine space이다.

벡터와 포인트를 함께 표기하기 위한 방법으로 동차 좌표계로 표기한다.
n차원의 벡터와 포인트를 표기시 n+1의 행렬을 사용하며
벡터일때는 마지막 요소가 0 포인트일때는 1을 사용한다고한다.

directx 에서 표기법은 아래와 같다

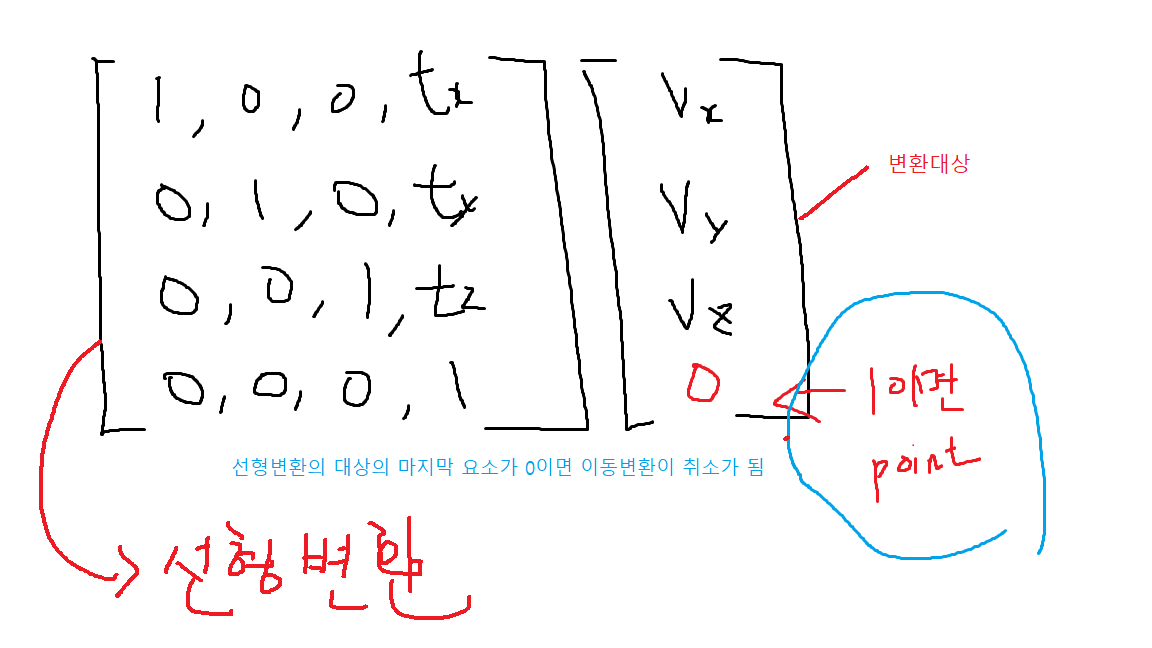
아핀변환의 특징은
그래프의 평행이동이 같은게 아니다라고 이해하고잇다
점,직선,면을 유지를 하고(점은 변환해도 점, 직선은 변환해도 직선, 면은 변환해도 면이라는 말)각 포인트간의 비율은 유지해주지만 거리와 각도를 유지하는건 아닌걸로 이해하고잇다.(현재는)

출처

• https://www.youtube.com/watch?v=DSmXIYkp024&t=8s
• https://en.wikipedia.org/wiki/Affine_transformation