[Billion-scale similarity search with GPUs] 논문 정리

📝 Billion-scale similarity search with GPUs

---

Abstract

• 유사성 검색은 고차원 데이터(예: 이미지, 비디오)를 다루며, GPU를 효과적으로 활용하는 것이 중요함

• 기존 GPU 기반 방법은 k-최소 선택과 메모리 계층 활용의 비효율성으로 인해 병목 현상이 발생함

• 본 연구에서는 이론적 최대 성능의 최대 55%까지 도달하는 k-선택(k-selection) 설계를 제안하며, 이를 통해 기존 GPU 기반 최근접 이웃(Nearest Neighbor) 구현보다 8.5배 빠른 성능을 달성함

• 완전 탐색, 근사 검색, 제품 양자화를 활용한 압축 도메인 검색을 최적화하여 기존 연구보다 뛰어난 성능을 보임

---

1 Introduction

• 이미지 및 비디오 검색에서 GPU 활용이 필수적이지만, 기존 접근법은 병목 현상이 존재함

• k-NN 그래프 구축은 대규모 데이터에서 연산 비용이 높으며, NN-Descent 등의 기존 방법은 메모리 오버헤드가 커서 확장성 부족이 문제임

• 제품 양자화(PQ) 방식이 이진 코드보다 유리하며, 이를 GPU에서 효과적으로 구현하는 방법을 연구함

• GPU에서 효율적으로 동작하는 k-선택 알고리즘을 개발하여, 기존 방법보다 성능을 크게 향상시킴

• 제안된 방법이 단일 및 다중 GPU 환경에서 기존 연구 대비 우수한 성능을 보임

---

2 PROBLEM STATEMENT

• 대규모 데이터셋에서 정확한 k-NN을 찾는 것이 계산적으로 비싸기 때문에 근사 최근접 이웃(Approximate Nearest Neighbor, ANN) 검색 기법을 사용하는 방식을 소개하고 있음

2.1 k-Nearest Neighbor Search (k-최근접 이웃 검색)

• 벡터 컬렉션에서 유사도를 기반으로 검색하는 문제를 다룸

• 주어진 쿼리 벡터 $𝑥∈𝑅^𝑑$ 와 컬렉션 내 벡터 $𝑦_𝑖 (𝑖=0,…,ℓ)$ 에 대해, L2 거리 기준으로 가장 가까운 k개의 벡터를 찾는 것이 목표

• 전체 데이터셋 크기는 1.4T 토큰이며, Wikipedia와 Books 데이터는 약 2 에포크 동안 학습됨

• 절대 위치 임베딩 대신 RoPE(Rotary Positional Embeddings)를 도입하여 성능을 개선함

2.2 k-Selection (k-선택)

• 배열 $[𝑎_𝑖]_{𝑖=0:ℓ}$ 에서 가장 작은 k개의 값을 찾는 연산을 수행함

• 코사인 유사도를 사용할 경우 최댓값을 찾는 방식으로 변경될 수도 있음

2.3 Batching (배치 처리)

• 검색 연산은 일반적으로 $𝑛_𝑞$개의 쿼리 벡터를 한 번에 처리함

• 병렬 처리를 활용하여 여러 CPU 스레드 또는 GPU에서 효과적으로 실행할 수 있음

• 각 쿼리에 대해 k개의 최근접 이웃을 선택하는 작업이 필요함

2.4 Exact Search (정확한 검색)

• 정확한 k-NN 검색을 수행하기 위해 모든 쿼리 벡터와 데이터셋 벡터 간의 거리 행렬을 계산해야 함

2.5 Compressed-Domain Search (압축 도메인 검색)

• 정확한 검색 대신 근사 k-NN 검색을 수행하며, IVFADC 구조를 사용함

2.6 Asymmetric Distance Computation, ADC (비대칭 거리 계산)

• ADC 방식은 근사 k-NN을 찾기 위해 양자화된 벡터를 사용해 거리 계산 수행

• IVFADC 방식에서는 첫 번째 양자화 $𝑞_1(𝑦)$ 를 기준으로 검색 대상 제한하여 계산 비용 절감을 달성함

2.7 Inverted File Structure (역방향 파일 구조)

• 데이터셋 벡터들은 $∣𝐶_1∣$ 개의 역방향 리스트로 그룹화됨

• 여기서 $𝐶_1$은 첫 번째 양자화 단계에서 생성된 클러스터 집합을 의미함

2.8 Quantization Methods (양자화 방법)

• 첫 번째 양자화 $𝑞_1$는 검색 속도를 위해 적절한 개수의 중심점을 사용해야 함 (예: $∣𝐶_1∣≈\sqrt{ℓ}$)

• 두 번째 양자화 $𝑞_2$는 메모리 사용 증가를 감수하고 정밀한 보정을 수행할 수 있음

2.9 Product Quantization (제품 양자화)

• 제품 양자화는 벡터를 여러 부분 벡터로 분할한 후, 각 부분을 독립적으로 양자화하는 방식임

• 이 방식은 연산량 증가 없이 매우 큰 양자화 코드북을 생성할 수 있음

---

3 GPU: OVERVIEW AND K-SELECTION

• Nvidia GPU 아키텍처와 프로그래밍 모델을 설명하며, 유사도 검색에서 GPU 활용이 어려운 k-선택 문제에 대해 논의함

3.1 Architecture

• GPU는 32개의 CUDA 스레드로 구성된 워프(warp) 단위로 명령을 실행하며, 워프 내 개별 스레드는 레인(lane) 이라고 불림

• 여러 워프가 모여 블록(block) 또는 CTA(Cooperative Thread Array)를 형성하며, 블록은 하나의 스트리밍 멀티프로세서(SM) 에 할당됨

• 블록들은 그리드(grid) 형태로 구성되어 실행되며, 실행 순서는 CPU에서 제어할 수 있음

3.2 GPU register file usage

• 레지스터를 많이 활용하면 실행 속도가 향상되지만, 블록 내 병렬 실행 개수가 줄어들어 점유율(Occupancy)이 낮아질 수 있음

• GPU 레지스터 파일은 용량이 커서 단순 연산뿐만 아니라 구조화된 데이터 저장소로 활용 가능함

• 워프 셔플(Warp Shuffle) 명령어를 사용하면 워프 내에서 레지스터 데이터 직접 공유가 가능하여 병렬 연산을 효율적으로 수행할 수 있음

3.3 k-selection on CPU versus GPU

• CPU에서는 Quickselect, Radix Selection, Bucket Selection 등의 알고리즘을 사용하지만, GPU에서는 전역 메모리 반복 접근으로 인해 효율성이 떨어짐

• GPU에서는 보통 작은 k값(보통 $k < 1000$)을 찾으며, CPU에서는 최대 힙(Max-Heap) 을 활용함

• GPU에서 힙 구현 시 분기(divergence)가 많아지고 데이터 이동이 비정형적이어서 성능 저하가 발생함

• 기존 GPU 우선순위 큐(priority queue) 기법은 동기화 비용과 커널 실행 오버헤드가 큼

---

4 FAST K-SELECTION ON THE GPU

4.1 In-register sorting

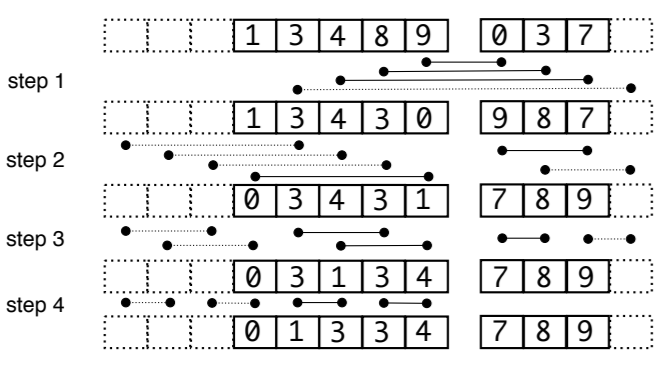
• Odd-size(홀수 크기) 병합 네트워크

  • 이미 정렬된 두 배열(왼쪽, 오른쪽)을 합치는 방식임

  • 배열 크기가 2의 거듭제곱이 아닐 경우, 다음 높은 거듭제곱으로 패딩하여 효율적인 정렬을 수행함

  • 첫 비교 단계에서 순서를 반대로 정렬하여 비트오닉 정렬을 단순한 단조 증가 정렬로 변환함

4.2 WarpSelect

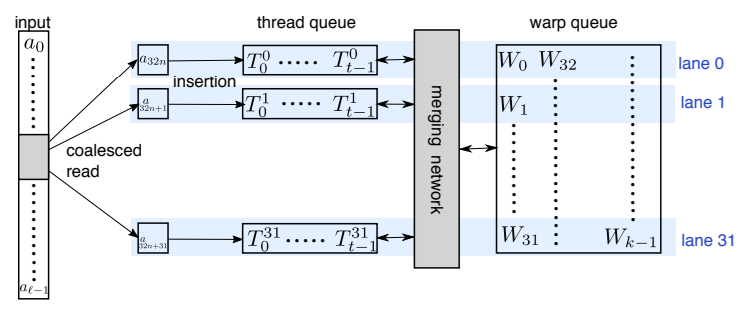
• WarpSelect는 k-선택을 위해 레지스터 내에서 연산을 수행하며, 한 번만 데이터 순회하고, 워프 간 동기화를 피함

• 기본 연산으로 merge-odd 및 sort-odd를 활용함

• 비동기식(asynchronous) 방식으로 처리하여 cross-warp 동기화를 피함

4.3 Complexity and parameter selection

• 한 번에 32개의 요소를 처리할 때, 다음 연산들이 수행됨:

  1. 32개의 요소를 읽고, 쓰레드 큐의 가장 큰 값과 비교 (비용 $C_1$, 횟수 $N_1$)

  2. 필요 시, 쓰레드 큐에서 삽입 정렬 (비용 $C_2 = O(t)$, 횟수 $N_2$)

  3. warp queue 갱신 시 병합 정렬 수행 (비용 $C_3 = O(t \log(32t)^2 + k \log(\max(k, 32t)))$, 횟수 $N_3$)

• 랜덤 데이터에 대한 실험 결과, 최적의 $t$ 값은 다음과 같음:

  • $k \leq 32 \rightarrow t = 2$

  • $k \leq 128 \rightarrow t = 3$

  • $k \leq 256 \rightarrow t = 4$

  • $k \leq 1024 \rightarrow t = 8$

---

5 COMPUTATION LAYOUT

5.1 Exact search

• 정확한 최근접 이웃 검색은 작은 데이터셋에 유용하며, 여러 인덱스 구성 요소로도 사용됨

• 행렬 곱셈(GEMM)을 활용해 거리 계산의 일부를 수행하고, fused k-selection 커널로 추가 최적화를 달성함

• 타일링과 멀티 스트리밍을 활용하여, 대규모 문제에서도 GPU 메모리 요구 사항을 줄이고 효율적으로 연산함

5.2 IVFADC indexing

• 제품 양자화(Product Quantization)를 활용해 벡터와 양자화 재현 값 사이의 거리를 빠르게 계산함

• 룩업 테이블(T1, ..., Tb)을 사전 계산하여 연산량을 크게 줄임

5.3 GPU implementation

• IVFADC의 GPU 구현은 타일링, 멀티 스트리밍, 그리고 커널 융합을 활용해 병렬성을 극대화함

• 타일 크기 $t_q$를 조절하여 메모리 사용을 최적화하며, 각 타일은 독립적으로 처리됨

5.4 Multi-GPU parallelism

• 복제(Replication): 인덱스가 단일 GPU 메모리에 맞는 경우, 여러 GPU에 복제하여 선형적 속도 향상을 얻음

• 샤딩(Sharding): 인덱스가 너무 커서 단일 GPU에 맞지 않는 경우, 데이터를 여러 GPU로 분산 처리함

• 복제와 샤딩 결합으로 더 많은 GPU 자원을 활용할 수 있음

• 샤딩은 복제보다 오버헤드가 발생하지만, 메모리 요구 사항이 줄어드는 장점이 있음

---

6 EXPERIMENTS & APPLICATIONS

• WarpSelect는 k-selection에서 기존 GPU 기반 방법(TBiS, fgknn)보다 최대 2배 이상 빠른 성능을 보이며, 특히 큰 k 값에서 성능 차이가 더욱 두드러짐

• k-means 클러스터링에서도 BIDMach보다 2배 빠르며, 다중 GPU 활용 시 선형에 가까운 속도 향상을 보여줌

• SIFT1M, SIFT1B, DEEP1B와 같은 대규모 데이터셋에서 근사 최근접 이웃 검색을 수행해, 기존 방식보다 높은 정확도와 최대 8.5배 빠른 속도를 기록함

• k-NN 그래프 생성에서도 GPU 기반 접근 방식이 CPU 기반 방법보다 훨씬 빠르며, 이미지 간 경로 찾기와 같은 응용 분야에서도 효율적으로 활용됨

---

7 CONCLUSION

• GPU는 테라플롭스(teraflops) 수준의 연산 처리 성능과 수백 GB/s의 메모리 대역폭을 제공하지만, 이를 최대한 활용하는 알고리즘 구현은 복잡함

• 본 연구에서는 GPU에서 최적에 가까운 성능을 달성하는 유사성 검색 알고리즘 구조를 제시함

• 이 접근 방식은 CPU나 클러스터보다 더 짧은 시간 내에 정확한 k-평균 클러스터링과 k-NN 그래프 생성이 가능하도록 함

• 머신 러닝 외에도 데이터베이스 애플리케이션에서 GPU 활용을 촉진하며, 논문 알고리즘의 엔지니어링 구현도 공개됨

---