Classification Task, Recommendation Task의 GCN 차이
-Classification Task는 노드 자체에 rich semantic feature를 가지며 Recommendation 경우 User or Item idex를 Random 초기화하여 사용하기 때문에 index를 통한 정보가 많지 않음
-즉, Rich semantic 정보가 없는 Recommendation Task에서 기존 GCN 구조를 사용하는 문제점을 제기함
NGCF: Neural Graph Collaborative Filtering
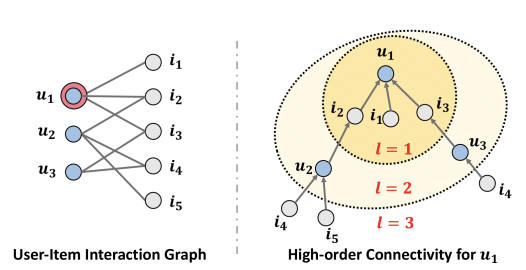
-NGCF는 Recommendation Task에 GCN 구조를 활용한 Collaborative Fitering 방법론이며 기존 GCN 구조를 차용한 선행 논문이다.
-NGCF는 User-Item matrix를 이분할 그래프로 표현함
-즉, 이분할 그래프를 통한 graph propagation이 일어나는 graph network를 만들었다.
-Layer를 쌓을수록 item을 통해 user가 표현되고 user를 통해 item이 표현되는 것을 볼 수 있다.
NGCF의 GCN 구조
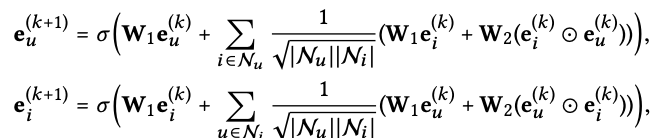
-NGCF의 GCN 구조는 기존 GCN 구조를 차용하는데 기존 GCN 구조는 trainable weight를 통한 Feature Transform, Layer를 쌓는 효과를 얻기 위한 non-linear activation이 있다.
-NGCF는 Collaborative Fitering 방법론을 위해 User와 Item의 임베딩을 따로 사용
LightGCN
Empirical Explorations on NGCF
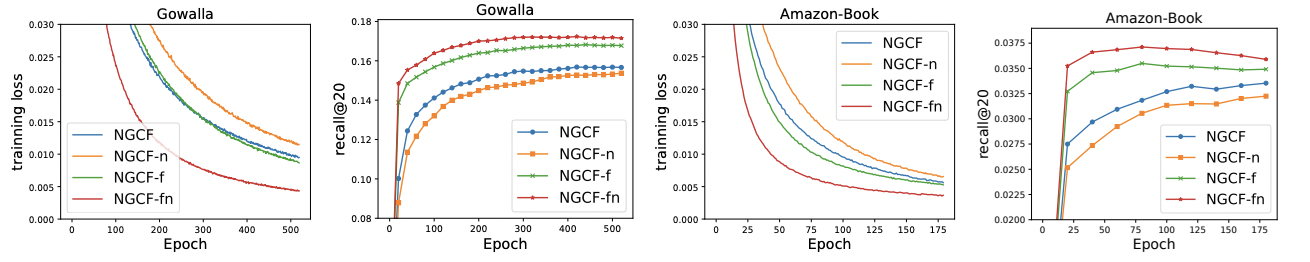

-LightGCN 저자들은 기존 GCN 구조를 차용한 NGCF의 방법론에 대해 실험을 진행
-즉, NGCF의 Feature Transform, non-linear activation이 Recommendation Task에 효과적인지 제거해 보며 확인
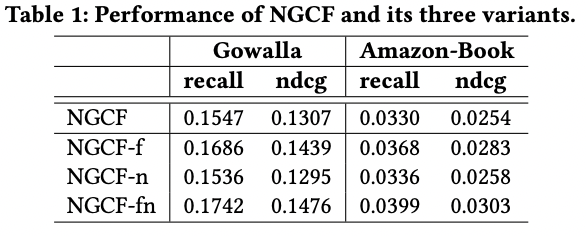
-결과적으로 feature transform은 성능을 저하시키며 feature transform이 있을 때, non-linear activation은 큰 효과가 없으며, feature transform이 없을 때는 안 쓰는게 좋음을 확인하였다.
-즉, 불필요한 연산이 성능저하를 야기 할 수 있음을 확인
LightGCN 구조
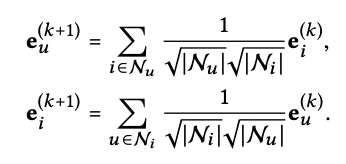
-LightGCN은 NGCF에서 사용한 weighted sum을 사용
-trainable weight와 non-linear activation을 제거
-즉, 처음 임베딩값에 대한 trainable parameter만 존재
-NGCF 임베딩에 사용된 self-connection을 사용하지 않음
-LightGCN 저자들은 각 layer의 output 값을 함께 사용하여 self-connection 효과를 얻는다고 수식적으로 증명
LightGCN Model
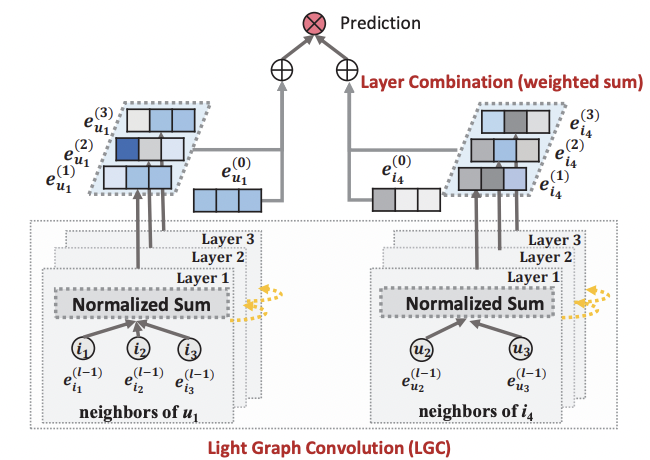
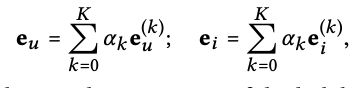
-가중치 알파를 통해 각 레이어 값들을 모두 뽑아옴(논문에서는 uniform 하게 사용)
-위 식을 통해 self-connection의 효과를 수식적으로 증명
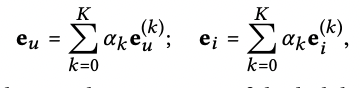
-최종적으로 생성되는 user와 item 임베딩의 내적값을 통해 도출
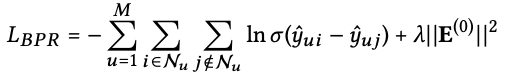
-LightGCN은 BPR loss를 사용하여 interaction이 없던 item에 score 값이 차이가 나도록 학습하고 앞서 설명한 바와 같이 trainable parameter는 초기 layer에만 있기 때문에 모델 복잡도는 Matrix Factorization과 동일하다고 설명하고 있음
LightGCN 수식적 증명(Relation with S-GCN)
LightGCN 최종 임베딩 벡터 도출식
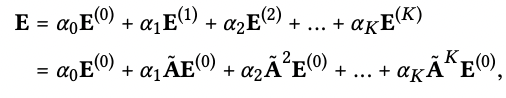
S-GCN에서 self-connection 적용
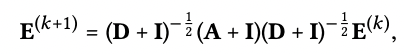
S-GCN에서 Scale 가중치 생략 후, 이항정리로 정리한 식
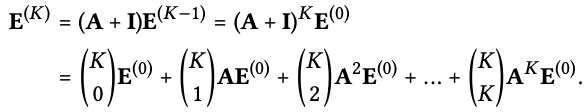
-LightGCN에서의 최종 임베딩 벡터 도출식과 S-GCN에서 가중치 생략후 이항정리 식이 똑같은 form을 하고 있음을 설명
-즉, 가중치 알파를 조정하여 self-connection 효과를 낼 수 있다고 설명함
LightGCN 수식적 증명(Relation with APPNP)
Over-smoothing
-GCN 구조의 문제점으로는 대표적으로 Over-smoothing problem이 있다.
-Over-smoothing은 그래프 신경망의 layer 수가 증가하면서 정점의 임베딩이 서로 유사해지는 현상을 의미한다.
APPNP
-Over-smoothing 문제를 해결 방법으로는 APPNP가 있다.
-이는 0번째 층을 제외하고는 신경망 없이 집계 함수를 단순화한 방식이다. 기존 층에서 층으로 갈 때 학습되던 𝐖를 0번째 층에서만 적용하고 나머지 층에서는 삭제한 뒤 집계함수를 단순화한 방식이다.
LightGCN에서 최종 임베딩 벡터 도출식
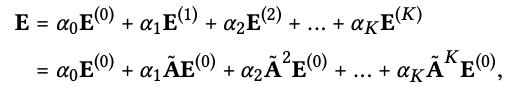
APPNP에서 최종 임베딩 식
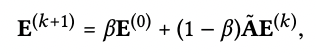
APPNP 정리식
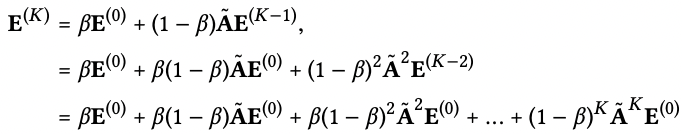
-LightGCN 최종 임베딩 벡터 도출식과 Over-smoothing problem을 해결 할 수 있는 APPNP의 식이 똑같은 form을 하고 있는 것을 수식적으로 증명함
Analysis of Embedding Smoothness
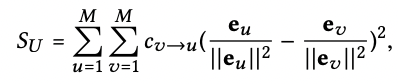
-LightGCN 저자들은 interaction이 발생 했을 때 얼만큼 유사한 임베딩 공간에 놓여지는지를 보기 위해 위 식을 정의함
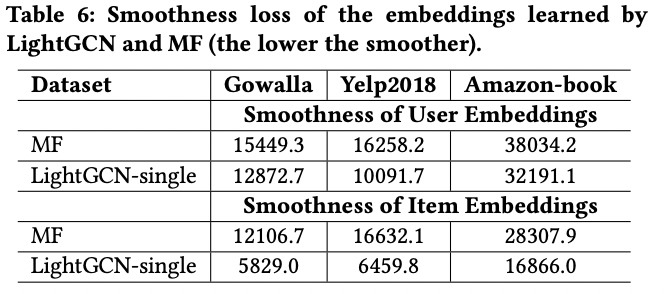
-MF와 비교하였을 때 결과적으로 더 낮은 Smoothness 값을 보이며 이는 LightGCN에서 임베딩이 더 부드러워지고 추천 시스템에 적합하다고 저자들은 설명함
NGCF vs LightGCN
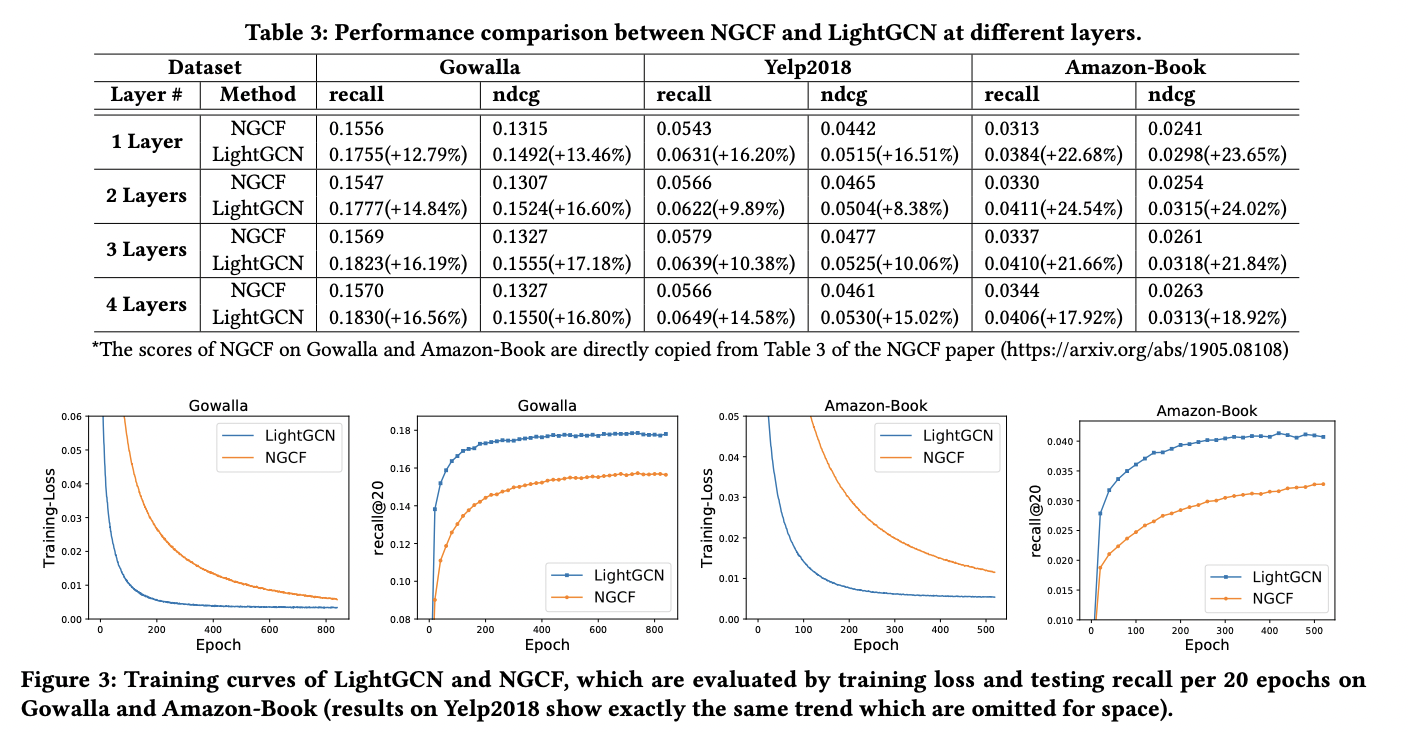
-Train loss를 보면 LightGCN이 더 빠르게 줄어드는 것을 확인 할 수 있다.
-이는 모델이 더 가볍다고 볼 수 있다.
-또한 NGCF는 hyperparameter 튜닝을 통해 LightGCN 보다 더 Train loss를 줄일 수 있지만 Train loss를 통해 추천을 하는 것이 아닐뿐더러 Train loss를 줄이는 것이 항상 좋은 recall 값을 가지는 것이 아님
Performance Comparison with sota
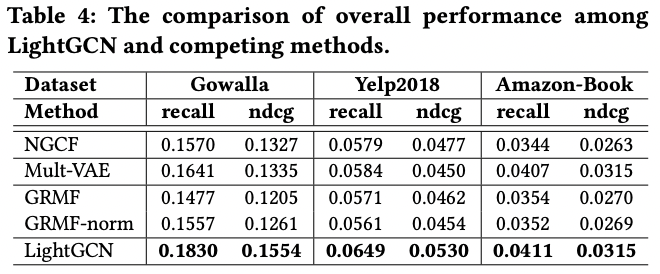
-LightGCN은 다른 세 가지 데이터셋에서 모두 다른 모델들 보다 좋은 성능을 보이는 것을 확인 할 수 있음
-또한 저자들은 LightGCN의 α값을 조정하여 더 좋은 성능을 낼 수 있다고 설명함
결론
-추천 시스템에서의 기존 GCN 구조의 문제점을 실험적으로 확인하고 이후 간단한 모델을 통해 좋은 성능을 내는 것을 확인할 수 있었다.
-또한, GCN 구조의 문제점인 Over-smoothing problem과 self-connection 효과를 수식적으로 증명한 것이 인상적이었다.
-Smoothness 값을 통해 유사한 임베딩을 확인 및 비교한 실험이 흥미로웠다.