Matrix Factorization
-rating matrix를 P와 Q로 분해
𝑅 ≈ 𝑃 × 𝑄^T = 𝑅
𝑃→ |𝑈| × 𝑘
𝑄→ |𝐼| × 𝑘
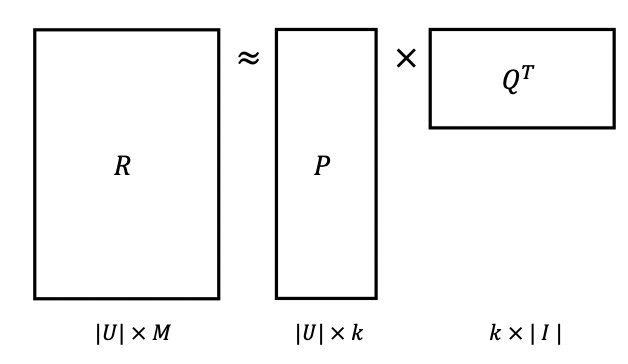
-평점 예측: 𝑟̂ =p^Tq
학습
r과 𝑟̂이 최대한 유사하도록 P,Q 학습
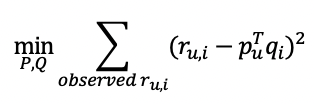
Matrix Factorization 최적화
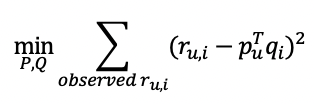
목적 함수를 정의하고 이를 minimize하는 optimization 수행
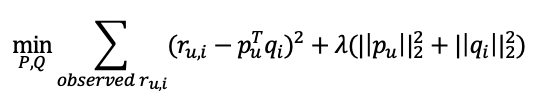
-𝑟 : 학습 데이터에 있는 유저 u의 아이템 i에 대한 실제 rating
-Pu: 유저 u의 latent vector
-Qi: 아이템 i의 latent vector 이는 최적화 문제를 통해 업데이트되는 파라미터
-𝜆 term: L2 Regularization(정규화), 𝜆:하이퍼 파라미터로 크기에따라 영향도가 달라짐(너무 크면 underfitting 발생)
(Regularization은 Loss에 weight의 크기를 고려하여 과적합을 방지하는 방법)
Stochastic Gradient Descent
-Gradient는 Loss를 wieght로 편미분하여 구할 수 있다. 이때 gradient는 수학적으로 항상 가파른 방향으로 향하기 때문에 Gradient의 반대 방향으로 update하여 Loss를 줄일 수 있다.
-기존 Gradient Descent는 모든 데이터를 고려하기 때문에 느리고 local minimum에 빠질 수 있다는 단점이 있다.
-이러한 단점을 완화하기 위해 SGD는 데이터 하나를 랜덤으로 뽑아 gradient를 구한 후 update 이러한 과정을 반복하여 기존 GD 단점을 극복한 optimizer 이다. 즉 하나의 데이터만 보고 방향을 빠르게 결정한다.
(SGD 또한 local minimum에 빠질 수 있지만 local munimum에서 빠질 수 있는 기회가 있다.)
MF with SGD
-실제 rating과 예측된 rating의 차이를 에러로 정
-Error:
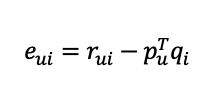
-Gradient:
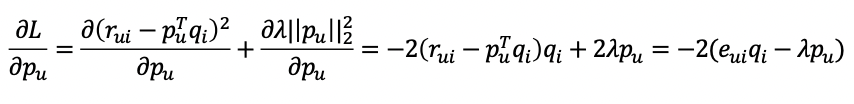
-Gradient의 반대방향으로 update:
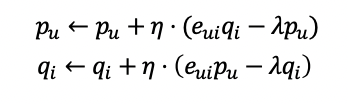
𝜂: learning rate
Adding bias
-adding bias function
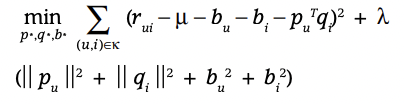
-유저가 아이템에 대해 편향이 있을 수 있다. 즉 bias를 추가하여 예측성능을 높임