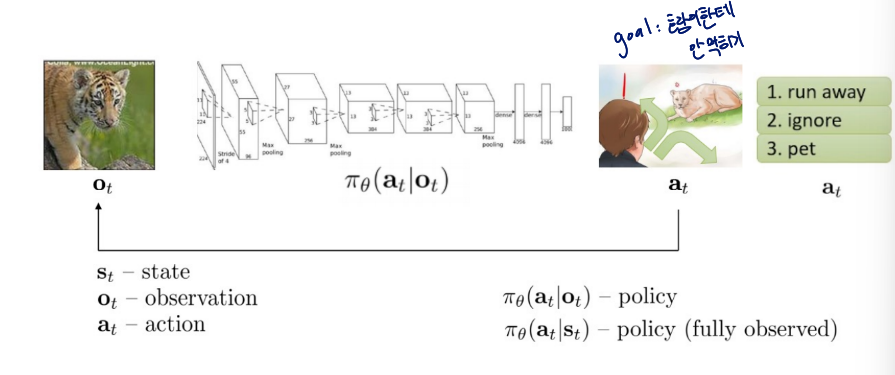
Terminology & notation
- : state
Markov property 만족 - : observation
how the agent see the world
Markov property를 만족하지 않음 - : action
- : policy
- : policy (fully observed)
action과 observation/state를 map한 것
어떻게 map 시킬지, 주어진 상황에서 어떻게 행동할지 학습
input : observation
output : action
t : time
Markov property
과거는 미래에 영향을 미치지 않는다! 라는 이론
- state가 markov property를 따른다는 걸 보여주는 예시
- 과거에 내가 백수였던 거 상관 없이 지금의 나는 직장인이다.
대강 이런 느낌.....
- 과거에 내가 백수였던 거 상관 없이 지금의 나는 직장인이다.
- observation이 markov property를 따르지 않는다는 것을 보여주는 예시
- 과거에 호랑이가 보였다가 지금 자동차에 가려졌다. 미래에 호랑이가 보이는 건 그러면 과거의 observation의 영향을 받은 것.
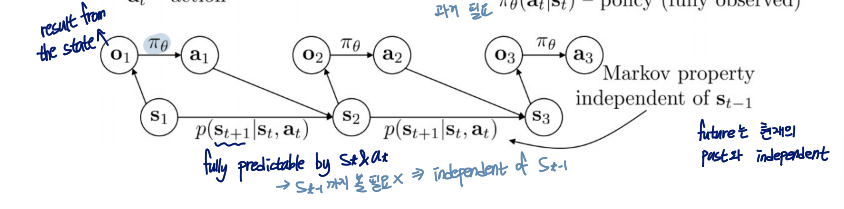
RL은 sequential decision problem
Imitation Learning
behavioral cloning 방법을 사용한 learning
어떤 것을 할 때, 중간중간 상황의 데이터를 수집+라벨링을 한 뒤 이를 기반으로 학습하는 것
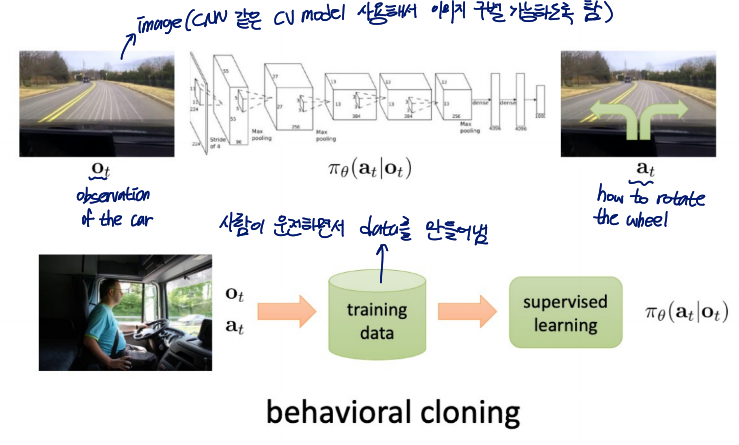
Does it Work?
아니용
초반에 작은 mistake만 해도 후에 큰 차이가 나게 됨
→ 전체적 흐름이 달라짐
train 시 본 적이 없었던 상황이 등장해서 예측이 갈수록 틀려지는 것
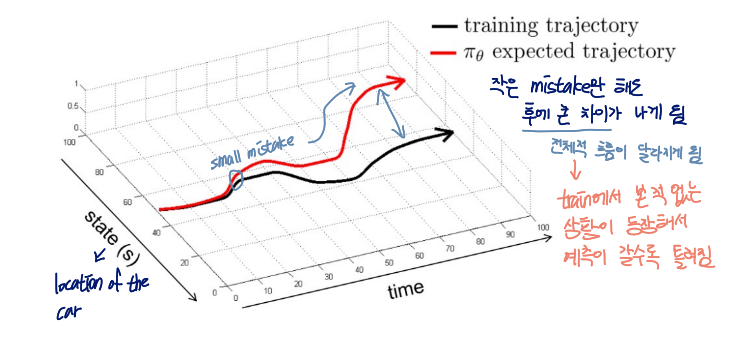
극복법
- 자율주행차의 경우, 한 개의 각도가 아닌 3개의 각도에 카메라를 사용
→ 각각 각도의 데이터 수집. 바퀴의 각도를 어떻게 할지 학습할 수 있게 됨 - lots of(diverse) trajectory를 학습
더 많은 데이터를 통해 mistake를 correct할 수 있도록 함
복기!
훈련한 모델을 실행할 때,
- distribution of train data = distribution of test data
→ work well - distribution of train data != distribution of test data
→ 처음에 작은 실수라도 하면 갈수록 work worse
실수하면 다음 상황들이 train distribution과 달라지기 때문
이런 문제를 해결하기 위해 로 만들 수 있을까?
는 distribution of something이라는 뜻
Can we make it work more often?
과 는 basicly diffrent하기 때문에 둘을 동일하게 만들 수는 없지만..
에 빠싹해지는 것보다 에 대해 빠싹해지자!라는 아이디어로
DAgger:Dataset Aggregation
이라는 기법 탄생!
GOAL
collect training data from intead of
이때 데이터는 를 돌리면서 수집 + label 필요
방법
- train from human data
- run to get dataset
- ask human to label with actions
- Aggregate:
- 반복
정리해보자면... 학습하면서 발생하는 새로운 상황(observation)들에 대해 또 적절한 답을 사람이 매겨주고 이를 사용하여 다시 학습하는 것
이론적으로는 좋지만 time consuming이 높아서 실용적으로는 좋지 않은 방법임
Deep imitation learning in practice
What might we fail to fit the expert?
1. Non-Markovian behavior
사람의 뇌는 과거의 일도 고려하여 행동함
→ state의 Markovian behavior assumption에 오류
- Markovian behavior의 경우
behavior depends only on current observation
만약 같은 것을 두 번 본다면, 과거에 무슨 일이 있었든지 같은 행동을 두 번 할 것임 - Non-Markovian behavior의 경우
behavior depends on all past observations
사람은 과거의 모든 일들을 고려하기 때문에 다른 행동을 할 수도 있음
Markovain behavior에 적혀있는 것이 often very unnatural for human demonstrators
Non-Markovian behavior를 위해서는..
- informations so far을 기억해야 함 → history 전부 input으로 사용
- time step에 따라 history의 길이가 달라서 input size가 fix되지 않는 문제 발생
→ RNN을 사용해서 해결!
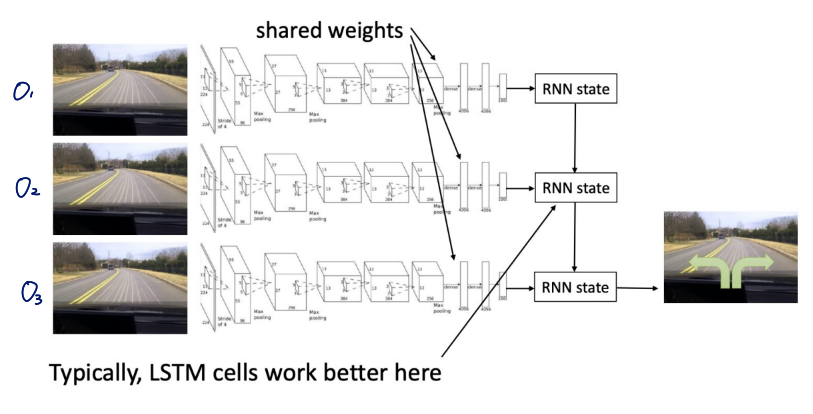
- time step에 따라 history의 길이가 달라서 input size가 fix되지 않는 문제 발생
Causal confusion
Non-Markovian behavior로 인해 에이전트는 보상이나 결과의 실제 원인에 대해 혼동
로 학습하는 경우인듯
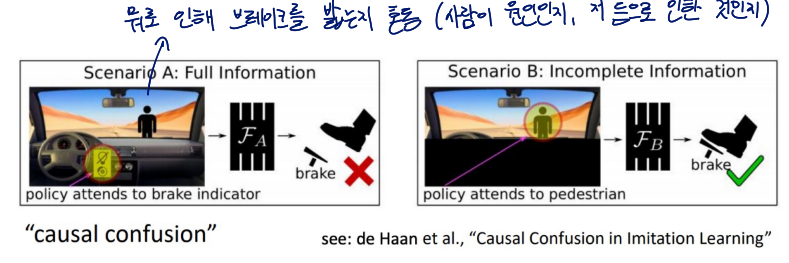
- Does including history mitigate causal confusion?
- YES
과거의 기억들을 통해 완벽은 아니지만 혼동을 개선할 수 있음
- YES
- Can DAgger mitigate causal confusion?
- YES
additional human judgement를 통해 개선 가능
- YES
그러나 including history와 DAgger 모두 causal confusion을 totally 개선하는 것은 불가능함
2. Multimodal behavior
어떤 상태에서 최적 또는 적절한 행동이 여러 개 존재할 때 발생
전문가의 데모가 여러 행동을 포함하는 경우, imitation learning model은 그 중 하나만을 선택하거나 평균적으로 학습하는데...
예를 들자면, 나무가 정면에 있어서 좌, 우로 피할 수 있는 상황에서 평균을 취해서 정면을 선택하게 됨 → 망함
이런 상황이 발생할 수 있어서 선택하는 방법을 잘 설정해야 됨
multimodal behavior의 경우에 행동을 선택하는 방법
-
Output mixture of Gaussians
sampling해야 되는 파라미터 :
# of distribution이 높아질수록 필요한 parameter 수 증가
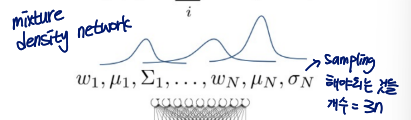
- model is simple → 모델링이 쉽다
- high dimensionality → 복잡한 분포의 표현이 어려움
-
Latent variable models
잠재변수를 사용해 복잡한 데이터 분포를 학습 또는 모델링하도록 함모델들 예시
2.1 Conditional variational autoencoder
2.2 Normalizing flow/realNVP
2.3 Stein variational gradient descent장점
- can actually represent distribution
복잡한 분포 표현 가능단점
- 구현이 매우 어려움
-
Autoregressive discretization
bin을 설정해서 distribution을 categorical로 변경만약 신체 각 부위를 움직이는 상황이라면 : 손가락 각도, : 팔꿈치 각도, ... 설정 후 각각의 Network에서 각 action을 예측하도록 함
한 번에 몽땅 하는 게 아니라 autoregressive하게 해서 복잡도를 줄임, →
특징
- good valance between simplicity & explicity
output mixture of Gaussians와 Latent variable models의 절충안 느낌으로 가우시안보다 복잡한 분포를 표현 가능하면서 구현이 latent variable model보다 쉬움
- good valance between simplicity & explicity
Imitation learning: recap
Often (but not always) insufficient by itsels
Distribution mismatch problem
Sometimes work well
- Hacks (e.g. left/right images)
- Samples from a stable trajectory distribution
- Add more on-policy data (e.g. using DAgger)
- Better models that fit more accurately
Cost functions, reward functions and a bit of theory
What's the problem of Imitation learining?
- Humans need to provide data, which is typically finite
딥러닝은 데이터가 plentiful할 때 work best - Humans are not good at providing some kinds of actions
- Humans can learn autonomously
- unlimited data from own experience
- continuous self-improvement
machine이 하기에는 어려운 과제
Terminology & notation
위의 상황에서 Cost function
먹히면 cost가 높아지도록 수식 설정
로 하여 cost function이 penalty가 될 수 있도록 함
s : state, a : action, r(s,a) : reward function
x : state, u : action, c(x,u) : cost function
A cost function for imitation
: human(optimal)
Some analysis
why imitation learning is not that good?
making a mistake의 확률을 매우 작은 숫자로 잡아서
assume:
for all
→ T가 증가할수록 실수할 확률이 제곱으로 늘어나게 됨
Another way to imitate
Goal을 정하지 않고 원하는 곳에 가는 데이터를 수집하여 학습
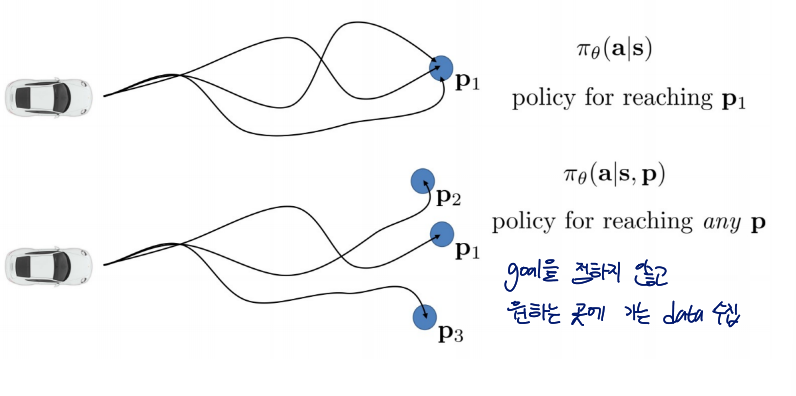
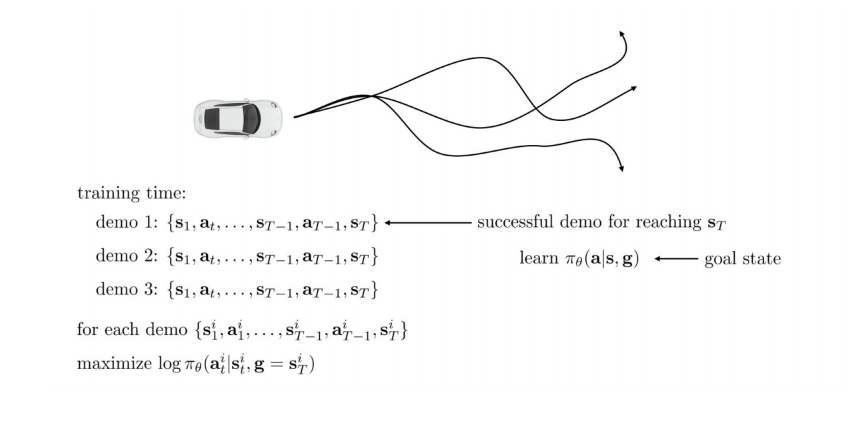
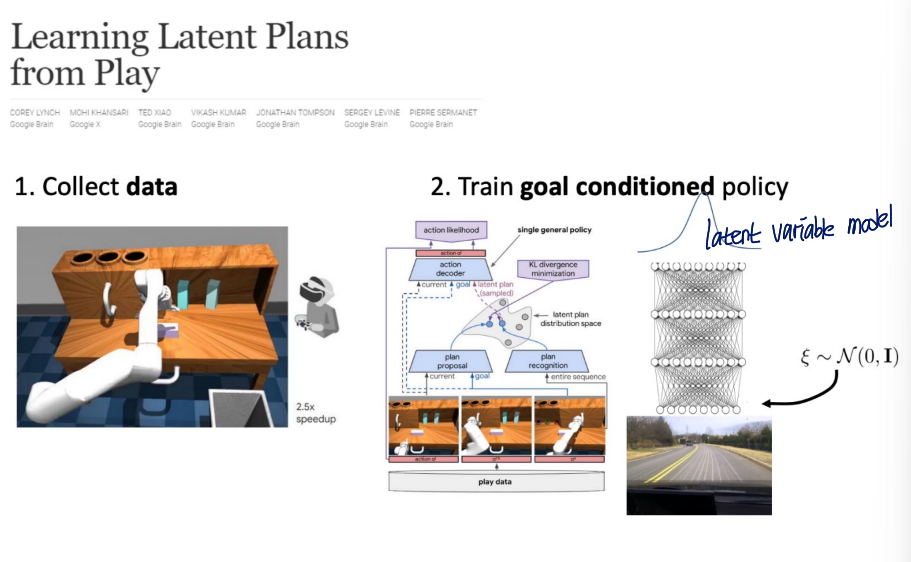
Latent variable model을 통해 multimodal behavior를 해결
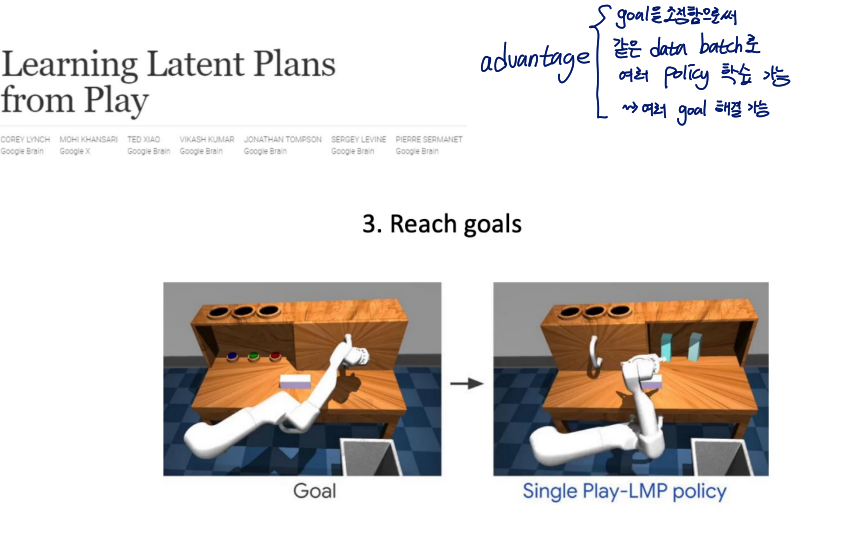
Going beyond just imitation?
- start with a random policy
- collect data with random goals
- treat this data as "demonstrations" for the goals that were reached
- use this to improve the policy
- repeat