2. Introduction of Reinforcement Learning (Key Concepts of RL)

Recap

Basic of Reinforcement Learning

• Input
  given environment which provides numerical reward signal, and agent which act inside of that environment
• Outputs
  let agent learn how to take actions(policy) in order to maximize reward
  policy는 goal을 달성하기 위한 strategy or skill
• Goal
  learn how to take actions in order to maximize reward
• Design RL
  Objective, State, Action, Reward
  objective : goal, state : description of the world로 이해하면 됨

Design RL예시

1. 
   

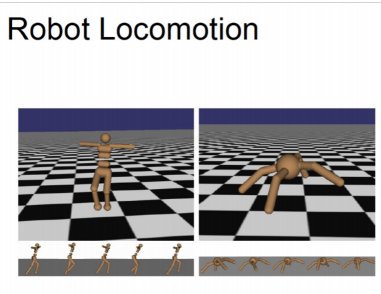
   • objective : 로봇이 앞으로 움직이도록 만들기
   • state : joints의 각도와 위치
   • action : joints에 apply될 torques
   • reward : 1 at each time step upright + forward movement

2. 
   

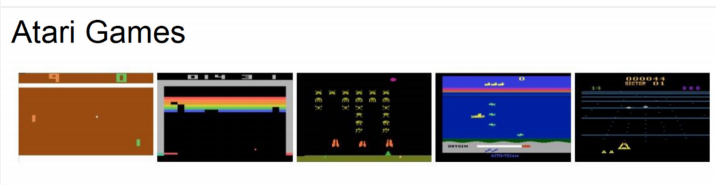
   • objective : complete the game with the highest score
   • state : raw pixel inputs of the game state
   • action : game controls (e.g. left, right, up, down)
   • reward : score increase/decrease at each time step

3. 
   

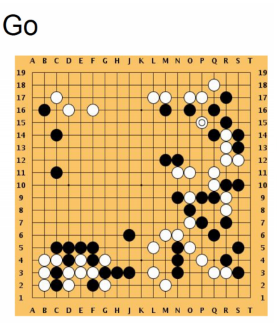
   • objective : 바둑 우승
   • state : 각 바둑돌들의 위치
   • action : 다음 돌을 어디에 놓을지
   • reward : 승리 시 1, 패배 시 0

Key Concepts in RL

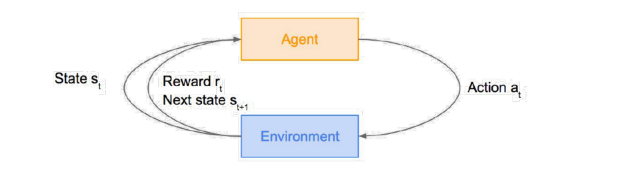
State ($s$)

A complete description of the state of the world(environment)

Action ($a$)

Agent take action on the environment
주어진 환경에서 가능한 액션의 집합을 action space으로 부름 (discrete/ continuous)

Reward ($r$)

The agent also perceives a reward signal from the environment, a number that tells it how good or bad the current world state is.

Trajectories ($\tau$)

world에서 state와 action, reward의 시퀀스

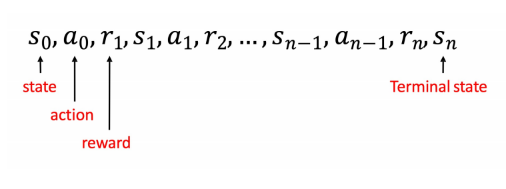
Meaning of Life for RL Agent

: Maximize Reward

주어진 trajectory $\quad s_0,a_0,r_1,s_1,a_1,r_2,...,s_{n-1},a_{n-1},r_{n},s_n$

• Future reward:$\quad R_t = r_t+r_{t+1}+r_{t+1}+...+r_n$
  Markov property를 따라 이미 일어난 일은 고려 안함 → future reward를 maximize하고자 함
• Discounted future reward: $\quad R_t = r_t+\gamma r_{t+1}+\gamma^2 r_{t+1}+...+\gamma^{n-t}r_n$
  $\gamma$는 discount factor
• agent의 좋은 strategy는 언제나 (discounted) future reward를 최대화하는 action을 선택하는 것
• Why "discounted"?
  • analyze convergence를 돕는 수학적 트릭
  • environment stochasticity의 불확실성
    미래는 멀수록 더 불확실해지므로 갈수록 리워드를 적게 고려하는 가중치를 곱하는 것

RL이 directly or indirectly 학습하려는 것

Policy

agent's behavior function

Value function

how good is each state and/or action

Model

agent's representation of the environment
Model $\neq$ Policy

각각에 대해 조금 더 깊이 알아보자면

Policy

• Agent's behavior function : A rule used by an agent to decide what actions to take
• Deterministic Policy: $a_t = \mu_\theta(s_t)$
  only one action is correct to take
• Stochastic Policy: $a_t \sim\pi_\theta(\cdot|s_t)$
  여러 action 가능
  • Categorical policies: discrete actions
  • Gaussian policies: continuous actions

Value Function

• 각 state and/or action이 얼마나 좋았는지에 대한 점수
• the expected cumulative return if you start in the state or state-action pair
  해당 state 또는 state-action pair에서 시작하는 경우의 예상 누적 수익률
• 거의 모든 RL algorithm에서 어떤 식으로든(one way or another) 사용 됨

Given Trajectory

$\tau = s_0, a_0, r_1, s_1, a_1,..., r_{n-1}, s_{n-1}, a_{n-1}, r_n, s_n$

Expected cumulative reward: $R(\tau) = \sum_{t=0}^{\infty}\gamma^tr_t$

• Value Function ($V^{\pi}(s)$)
  state $s$에서 시작하고 언제나 policy $\pi$를 따라 행동하는 경우의 예측값
  $V^{\pi}(s) = E_{\tau \sim \pi}\big[R(\tau) | s_0 = s\big]$
  간단하게 생각한다면, 현재 state 상황에서 가질 수 있는 future reward의 합이라고 생각하면 됨
• Action-Value Function ($Q^{\pi}(s,a)$)
  state $s$에서 action a를 하며 시작하고 언제나 policy $\pi$를 따라 행동하는 경우의 예측값
  $Q^{\pi}(s,a) = E_{\tau \sim \pi}\big[R(\tau)|s_0=s,a_0=a\big]$
  $s_t$에서 $a$를 취할 때 expected reward의 합

The RL Problem
RL의 목표는 agent가 따라 행동했을 때 expected cumulative reward를 최대화시키는 policy를 고르는 것
$\pi^* = \underset{\pi}{\mathrm{argmax}}(E\big[R(\tau)\big])$

• $s_0$이 주어진 경우 → $E\big[R(\tau)\big]$ : Value function (V)
• $s_0, a_0$이 주어진 경우 → $E\big[R(\tau)\big]$ : Q function (Q)

self-consistent Bellman Function을 통해 policy를 수치적으로 최적화(numerically optimize)시킬 수 있음