7. Value Function Methods

Can we remove policy gradient completely?

YES!

$A^\pi(s_t,a_t)$ : $a_t$가 다른 $\pi$에 따른 average action보다 얼마나 나은지에 대한 정보
복기해보자면 $A(s,a) = Q(s,a)-V(s)$로
V는 avrage action, Q와 V는 whether action is a or not만 다름

그러면
$\argmax_{a_t} A^\pi(s_t,a_t)$: $\pi$를 따를 때, $s_t$에서의 최고의 action
이는 basicly means policy $\Rightarrow$ policy 대신 사용!

따라서 forget policies, let's just do $\argmax_{a_t} A^\pi(s_t,a_t)$!

이때,
$\pi'(a_t|s_t)=\begin{cases}1 & \text{if }a_t=\argmax_{a_t}A^\pi(s_t,a_t)\\0&\text{otherwise}\end{cases}$
1과 0은 각각 probability
as good as $\pi$ (probably better)

이렇게 해가지고, 하나만 가지고 actor-critic algorithm이 작동할 수 있도록 변경됨!

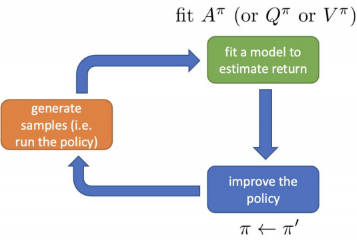
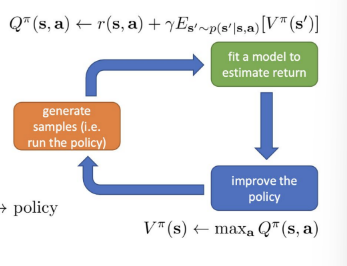
Policy iteration

High level idea

policy iteration algorithm

1. evaluate $A^\pi(s,a)$
   how to do this?
2. set $\pi\rightarrow\pi'$
   $\pi$ : theoritical policy
   $\pi'$ : implicit policy

$\pi'(a_t|s_t)=\begin{cases}1 & \text{if }a_t=\argmax_{a_t}A^\pi(s_t,a_t)\\0&\text{otherwise}\end{cases}$

as before: $A^\pi(s,a) = r(s,a) + \gamma E[V^\pi(s')] - V^\pi(s)$$\quad s' = s_{t+1}$

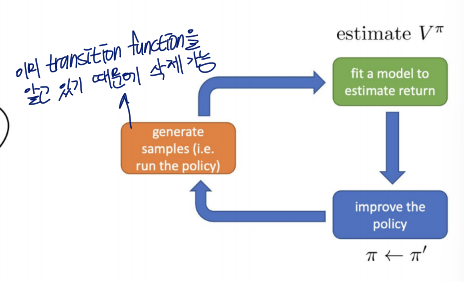
Dynamic Programing

one way to evaluate $V^\pi$
advantage function을 구하는 것은 value function을 구하는 것으로 formate될 수 있음

Assumption

we know

• $p(s'|s,a)$
  transition function ($\rightarrow$ assume we know the transition probability)
  원래 model-free RL은 transition function이 없음
  $\rightarrow$ model based function이라 가정 $\Rightarrow$ environment =의 dynamic을 알고 있음
• $s$ and $a$ are noth discrete (and small)
  dp 사용을 위한 가정

Example

• 16 states
• 4 actions
  up, down, left, right

$\Tau$ is $16\times16\times4$ tensor

bootstrapped update: $V^\pi(s)\leftarrow E_{a\sim\pi(a|s)}[r(s,a)+\gamma E_{s'\sim p(s'|s,a)}[V^\pi(s')]]$

• $E_{a\sim\pi(a|s)}$ : deterministic policy이므로 걷어낼 수 있음
• $V^\pi(s')$에는 just use the current estimate

$\pi'(a_t|s_t)=\begin{cases}1 & \text{if }a_t=\argmax_{a_t}A^\pi(s_t,a_t)\\0&\text{otherwise}\end{cases} \rightarrow\text{ deterministic policy } \pi(s)=a$

deterministic policy $\pi(s)=a$ : state에 따라 정해진 a들 존재하여 변화X

simplified: $V^\pi\leftarrow r(s,\pi(s))+\gamma E_{s'\sim p(s'|s,\pi(s))}[V^\pi(s')]$

policy iteration with dynamic programming

policy iteration

1. evaluate $V^\pi(s)$
2. set $\pi\leftarrow\pi'$

$\pi'(a_t|s_t)=\begin{cases}1 & \text{if }a_t=\argmax_{a_t}A^\pi(s_t,a_t)\\0&\text{otherwise}\end{cases}$

policy evaluation

$V^\pi\leftarrow r(s,\pi(s))+\gamma E_{s'\sim p(s'|s,\pi(s))}[V^\pi(s')]$
이걸 사용해서 위의 iteration의 1 수행

Simplify A function

$\pi'(a_t|s_t)=\begin{cases}1 & \text{if }a_t=\argmax_{a_t}A^\pi(s_t,a_t)\\0&\text{otherwise}\end{cases}$

• $\argmax_{a_t}A^\pi(s_t,a_t) = r(s,a)+\gamma E[V^\pi(s')]-V^\pi(s)$로, too much equations!
  • $V^\pi(s)$는 constant로 ignore 가능
    $\rightarrow\argmax_{a_t} A^\pi(s_t,a_t) = \argmax_{a_t}Q^\pi(s_t,a_t)$
  • $Q^\pi(s,a) = r(s,a)+\gamma E[V^{\pi}(s')]$ (a bit simpler)

skip the policy and compute values directly!

$\Rightarrow$ value iteration algorithm

1. set $Q(s,a)\leftarrow r(s,a)+\gamma E[V(s')]$
   estimate all $Q(s,a)$ value
2. set $V(s)\leftarrow\max_a Q(s,a)$
   V는 expected reward at state s. argmax 통해 update

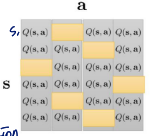
이렇게 행이 state이므로 각 행마다의 최댓값을 선택해서 V update