Boundary Detection

Boundaries of Objects

Boundaries of Objects

Human annotated boundaries

원래 안 보이는 부분까지 boundary를 그리는데 여기서는 그리지 않음

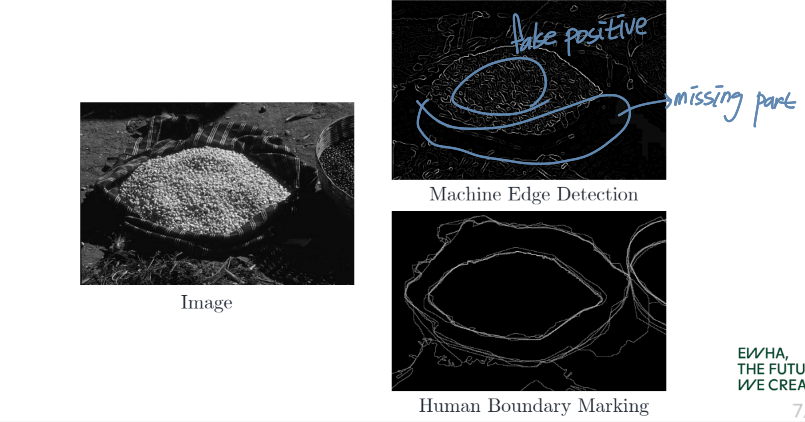
Edge detection

boundary를 잘 찾지 못함

• 코끼리 간의 색이 비슷하여 두 개체 각각의 boundary를 detect하지 못함
• 오른쪽 코끼리 발 옆은 doundary로 detect되면 안 되는데 됨
  FP

Multi-scale edge detection

$\sigma$를 많이 사용하고 합쳐서 FP를 줄임

그러나 아직 부족한 부분 많음

Another example

Hough Transform for Line Detection

Hough Transform

structure를 탐지하는 것에 elegant method

• edge는 connected될 필요X
• complete strucre need not be visible
• Key Idea: Edges VOTE for the possible models
  투표를 많이 받은 곳이 물체의 위치로 선정

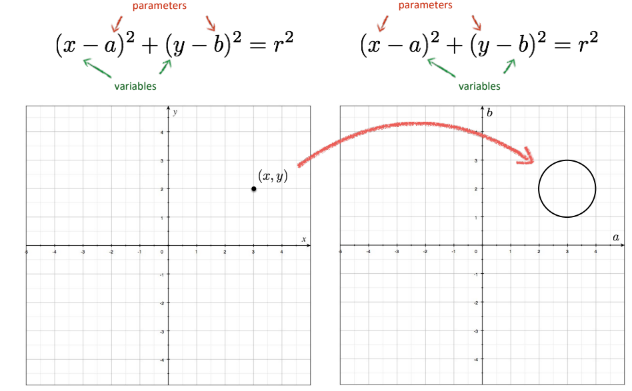
Image and Parameter Space

물체가 line인 경우,
물체에 대한 식을 $y=mx+b$로 표현할 수 있음

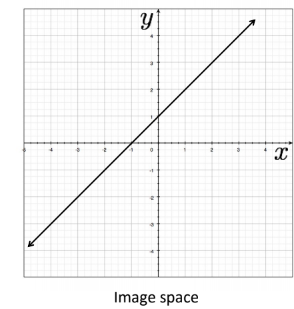
• variables : $y, x$
• parameters : $m,b$

이거를 parameter space로 바꾸면
식은 $y-mx = b$가 되고, line은 point가 됨

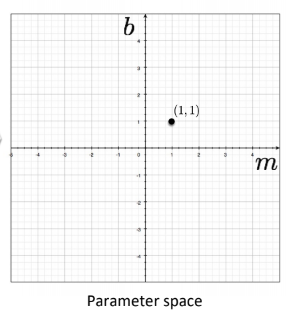
• variables : $m,b$
• parameters : $y,m$

Image space에서의 point는 Parameter space에서의 line이 됨
특정 한 점을 지나가는 1차함수는 다양하기 때문에

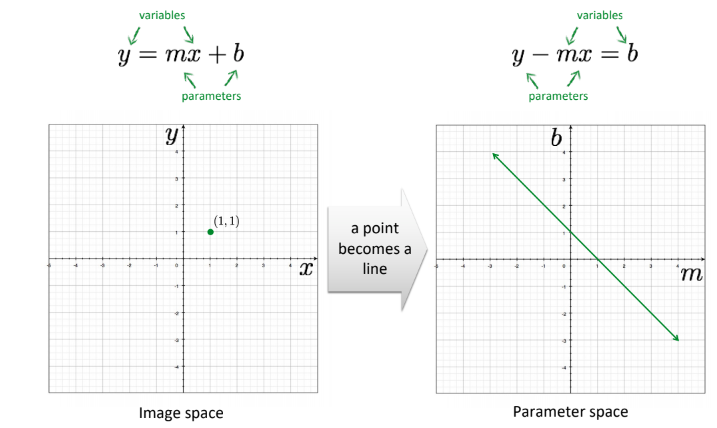
image space에서 두 점이 주어진 경우

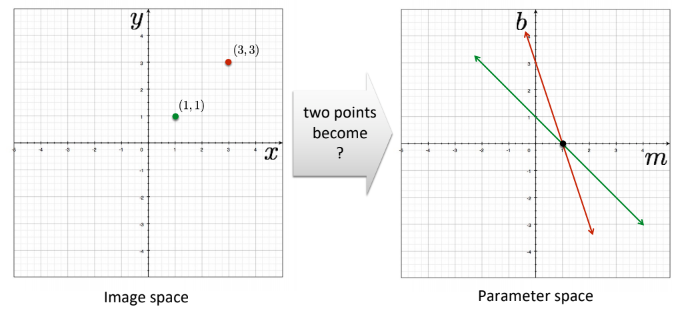
parameter space에서 crossing point가 적절 parameter 값

여러 개의 점이 주어진 경우 적절한 파라미터는 voting을 통해 선택할 수 있음
가장 많은 그래프가 교차하는 지점

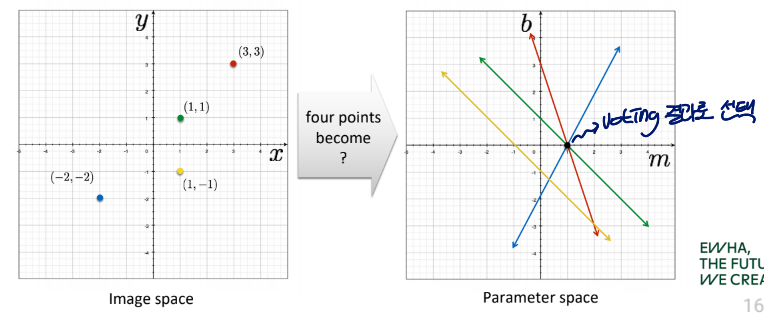
Line Detection by Hough Transform

Algorithm

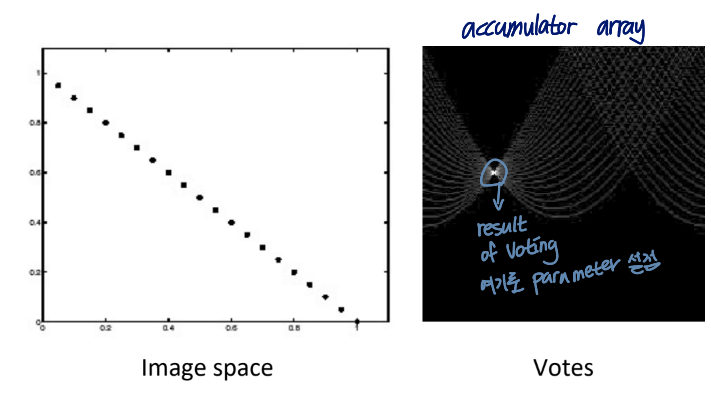
1. quantize parameter space (m,c)
   크기에 trade-off 존재
   quantize가 클수록 노이즈에 강함
2. create accumulator array A(m,c)
3. A(m,c)=0으로 설정 $\quad\forall m,c$
4. 각 이미지의 edge $(x_i,y_i)$에 따라 $A(m,c)=A(m,c)+1$$\quad \text{if (m,c) lies on the line }c=-x_im+y_i$
   그냥 line이 지나가는 칸들에 1씩 더하면 된다는 뜻
5. A(m,c)의 local maxima 찾기

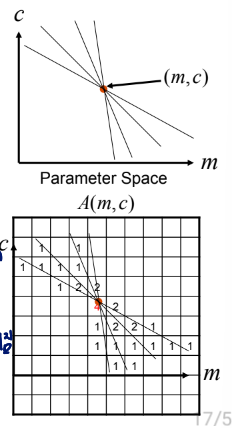
bin을 크게 설정하면 격자가 더 넓어짐

Better Parameterization

Note: $-\infty\leq m\leq\infty$

• accumulator가 너무 큼
• 메모리와 계산량이 많이 요구됨

Improvement

finite accumulator size 설정

• Line equation: $\rho = x\cos\theta+y\sin\theta\quad\quad\text{where} \begin{cases} 0\leq\theta\leq 2\pi \\ 0\leq\rho\leq\rho_{max} \end{cases}$
  

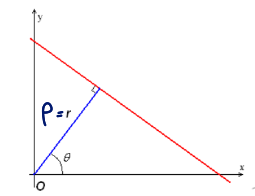
  • $\rho$ : line과 origin의 수직 거리
    $\therefore\rho_{max}$: 이미지의 대각선 길이

Image and Parameter Space

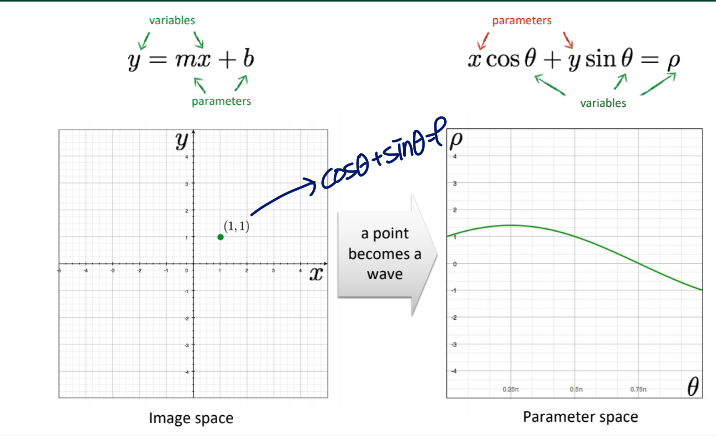
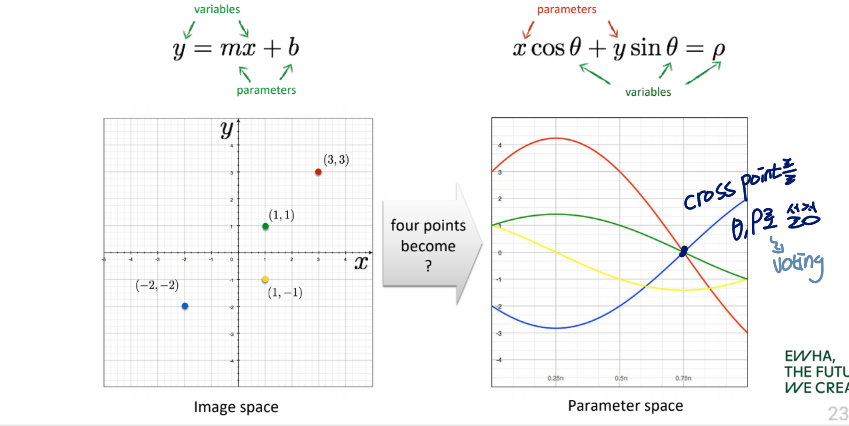
Image Space and Vote

Basic Shapes

뒤의 두 경우는 이미지에 선이 많은 경우
간단히 생각하면 local maxima의 개수가 line의 개수를 나타내고, 이에 따라 모양이 형성될 것

Real-World Example

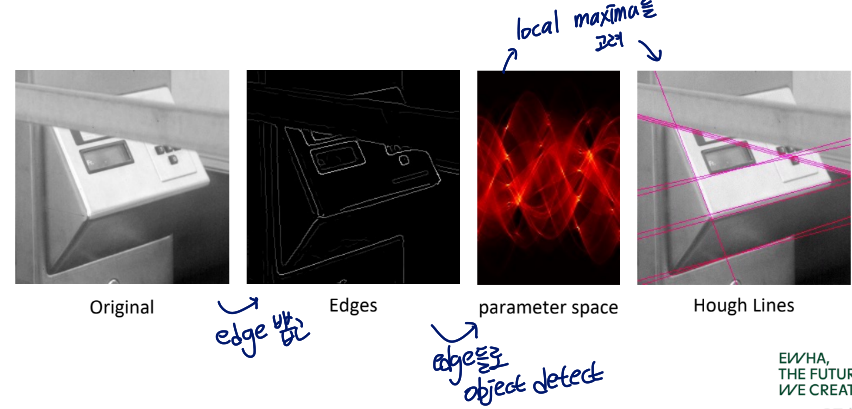
• original image에서 edge detection
• detect한 edge point들을 parameter space로 표현
• maxima들 뽑아서 그 값들을 사용해 boundary 형성

Mechanics of the Hough Transform

How many lines?

• count the peaks in the Hough array
• 인접한 peak를 single peak로 취급

Which points belong to each line?

• line에 가까운 점 찾기

Quantization error

• cells가 얼마나 커야 되는지
  크기에 따라 trade-off가 존재
  • Too big : 다른 line을 합치게 될 수 있음
  • Too small : line을 찾기 어려워짐
    large vote를 받은 bucket이 없어서 voting이 어려움

Difficulties of noise

measurements는 noisy함

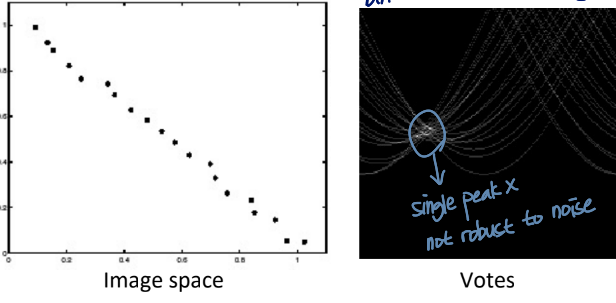
noise로 인해 single peak를 찾기 어려워질 수 있음
not robust to noise
bin의 크기를 키움으로써 해결할 수 있긴 한데,.. 노이즈가 너무 크면 이것도 잘 안 될 수 있음

noise가 증가할수록 fewer votes land in a single bin

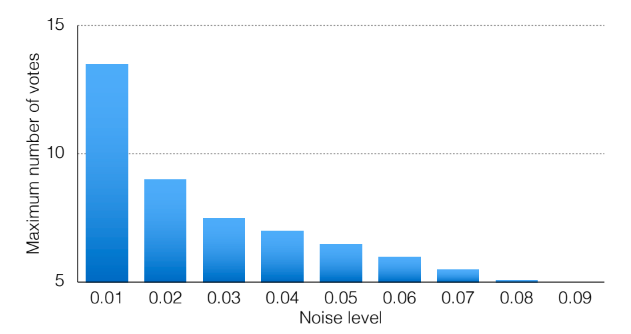
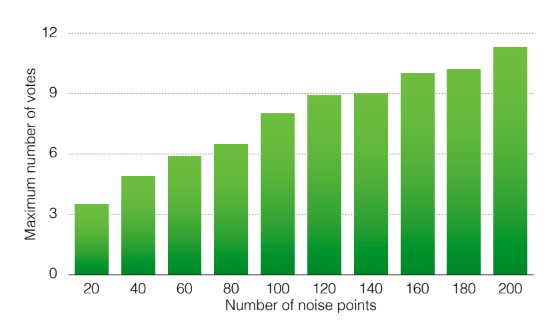
noise가 증가할수록 false peaks가 증가함

Hough Transform for Circle Detection

Finding Circles by Hough Transform

원형 물체에 대해 식을 표현하면
$(x-a)^2 + (y-b)^2 = r^2$

• For Image space
  • variables : $x, y$
  • parameters : $a,b,r$
• For Parameter space
  • variables : $a,b,r$
  • parameters : $x,y$

Let's assume radius known
$(x-a)^2 + (y-b)^2 = r^2$

• For Image space
  • variables : $x, y$
  • parameters : $a,b$
• For Parameter space
  • variables : $a,b$
  • parameters : $x,y$

Image and Parameter Space

이 경우, image space에서의 point는 parameter space에서 원이 됨

점이 여러 개 주어진 경우

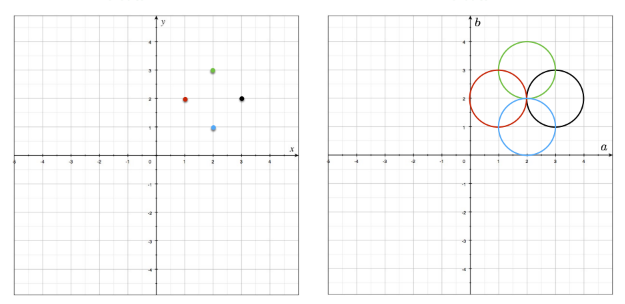
그리고 가장 많은 원이 교차하는 점이 파라미터로 채택됨

Finding Circles by Hough Transform

What if radius is unknown?

• 역원뿔 모양을 형성하게 됨
  
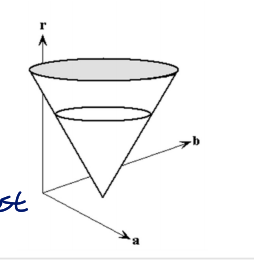
• 3차원 배열 사용 : A(A,b,r)
• parameter 수에 따라 size of accumulator와 computation이 exponential하게 증가하게 됨
  → need high computational cost

Using Gradient Information

Gradient information은 많은 양의 계산을 save할 수 있음

• Edge Location: $(x_i,y_i)$
• Edge Direction: $\phi_i$

radius에 대해 이미 알고 있다고 가정하면,

• $a=x-r\cos\phi$
• $b=y-r\sin\phi$

→ need to increment only one point in accumulator
compact해짐!

Finding Coins

동전 두 개의 size가 각각 주어짐

• 27 pixels
• 34.5 pixels

→ two different Hough transform with separate accumulators 하면 됨

• 큰 동전 용
• 작은 동전 용

Edge를 뽑아내고

Boundary detect

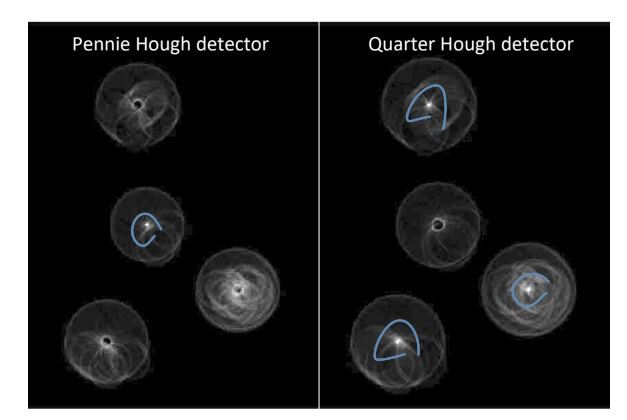
pennie 하나, quarter 3개 탐지

Generalized Hough Transform

Model의 shape가 방정식을 통해 표현이 안 되는 경우가 있음
silhouette only, random shape

Goal
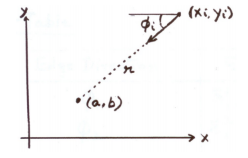
Find the object center $(x_0,y_0)$

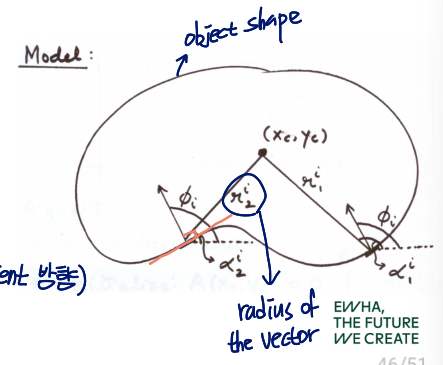
1. referent point $(x_c,y_c)$ 선정
2. for each point $(x_i,y+i)$ obtain $(r_i,\alpha_i,\phi_i)$
   • $r_i$ : a vector form from boundary point to reference $\vec{r_i}=(r_i,\alpha_i)$
   • $\phi_i$ : gradient 방향(orientation)
     즉, $(r_i,\alpha_i,\phi_i) = \text{(radius, angle, gradient 방향)}$

같은 direction을 가지는 vector들끼리 모은 table 생성

Algorithm

given edges를 통해 object center $(x_c,y_c)$를 찾고자 함
1. Accumulator Array A(x_c, y_c) 생성
2. Accumulator Array 초기화
3. For each edge point $(x_i,y_i,\phi_i)$

• For each entry $\vec{r_i} = (r_i, \alpha_i)$ in table, compute:
  • $x_c = x_i + r_k^i\cos\alpha_k^i$
  • $y_c = y_i + r_k^i\sin\alpha_k^i$
• Increment Accumulator: $A(x_c,y_c)=A(x_c,y_c)+1$

4. $A(x_c,y_c)$에서 local maxima 찾기

Scale과 각도도 고려해서 4차원 space에서 voting할 수도 있음

Hough Transform: Comments

사실 Hough Transform은 오래된 method라 요즘 많이 사용하지는 않음

Pros

• deals with occlusion well
• detects multiple instances
• robust to noise

Cons

• bad computational complexity
  object가 complex한 경우
• difficult to set parameters