Image ProcessingⅡ

Neighborhood Operations

근처의 픽셀까지 고려하여 이미지를 변환하는 방법

• Convolution
• Cross-Correlation
• Gaussian Smoothing
• Median Filter

Convolution

Integral of the product of the two functions after one is reversed and shifted

$h(x) =\underset{-\infty}{\overset{\infty}{\int}}f(\tau)g(x-\tau)d\tau \quad\quad h=f*g$

convolution 과정을 보자면

1. 
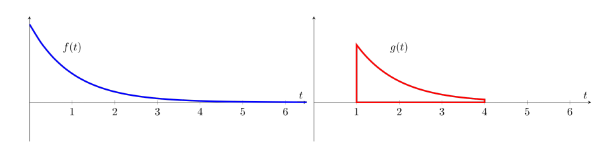
   dummy variable $\tau$에 따라 각 함수 표현

2. 
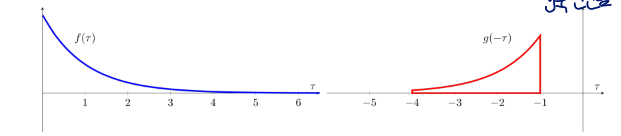
   reflect one of the functions $g → g(x - \tau)$
   g를 y축에 대해서 반전시킴

3. 
   $t$에 따라 그래프를 x축 방향으로 이동(slide시킴)

4. 
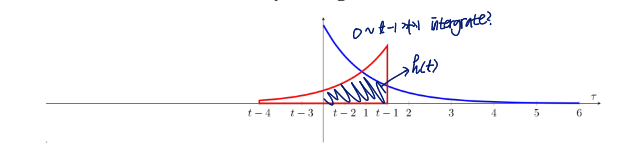
   두 함수가 겹치는 공간의 넓이가 바로 integral의 값

Properties of Convolution

formal definition of convolution에서만 해당하는 properties임
딥러닝과 같은 곳에서는 적용이 안 되는 경우도 있음
finite하기 때문..?

• Commutativity: $f * g = g * f$
  f: image, g: filter
  이건 딥러닝에서는 불가능하고, image processing에서만 가능한 property임
• Associativity: $f*(g*h) = (f*g)*h$
  order is not important하다는 뜻
• Distributivity: $f*(g+h) = (f*g)+(f*h)$
• Linearity: $f_1 \rightarrow \square \rightarrow g_1 \quad\quad f_2 \rightarrow \square \rightarrow g_2$
  $\quad\quad\quad\quad\alpha f_1 + \beta f_2 \rightarrow \square \rightarrow \alpha g_1 + \beta g_2$
  여기서 g는 convolution의 결과
• Shift invairance: $f(x-a) \rightarrow \square \rightarrow g(x-a)$는 $f(x) \rightarrow \square \rightarrow g(x)$를 x축 방향으로 a만큼 이동한 것
  

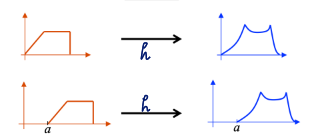
What $h$ will give us $g=f$?

Dirac Delta Fucntion (Unit Impulse)

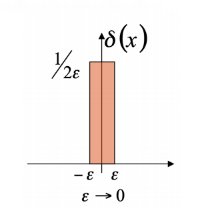
Sifting property:
kind of filtering property

$\underset{-\infty}{\overset{\infty}{\int}}f(x)\delta(x)dx =\underset{-\infty}{\overset{\infty}{\int}}f(0)\delta(x)dx \\ \quad\quad\quad\quad\quad\quad\quad=f(0)\underset{-\infty}{\overset{\infty}{\int}}\delta(x)dx = f(0)$

$g(x) = \underset{-\infty}{\overset{\infty}{\int}}f(\tau)\delta(x-\tau)d\tau = f(x)$

Discrete Convolution

$f(x,y) \rightarrow h(x,y) \rightarrow g(x,y)$

Image들은 사용하는 space가 dicrete하고 finite함
따라서 $g(i,j) = \underset{m=1}{\overset{M}{\sum}}\underset{n=1}{\overset{N}{\sum}}h(m,n)f(i-m,j-n)$
h: kernel, f: image

1. kernel(= filter = mask)를 horizontal and vertical direction으로 flip
2. 각 kernel의 value를 corresponding pixel value와 곱하고 합함
   
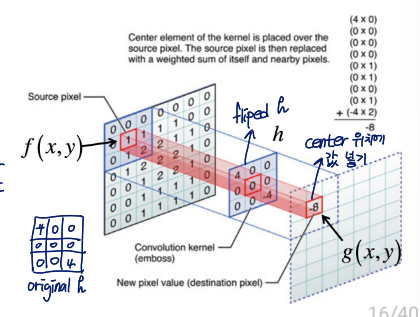
   그림에 나온 것처럼 center 위치에 구한 값 넣으면 됨

Border problem

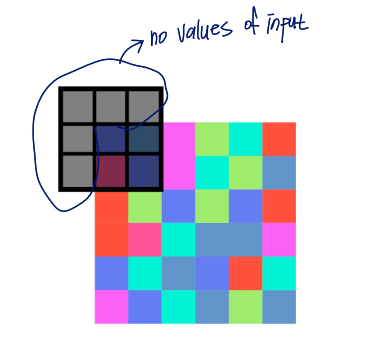
모서리 부근은 input으로 넣을 값들이 없는 문제 발생함

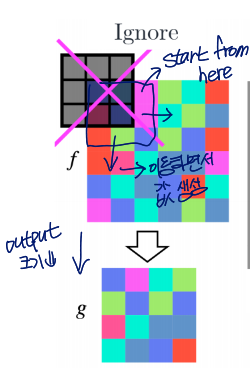
해결법

1. input으로 넣을 값들이 없는 위치는 convolution을 실행하지 않기(ignore)
   output 크기가 줄어드는 문제 발생
   
2. 원본 이미지를 padding 통해 size를 넓혀서 모든 위치 convolution 가능하도록 하기
   2.1 zero padding : 0으로 패딩
   
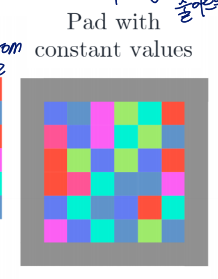
   2.2 reflection
   

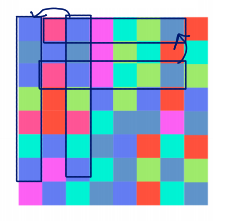
Cross-Correlation

템플릿을 알맞은 위치에 놓고자 함!

$\underset{i,j}{\mathrm{argmin}}E(i,j) = \underset{m=i+1}{\overset{i+M}{\sum}}\underset{n=j+1}{\overset{j+N}{\sum}}\big[f(m,n)-t(m-i, n-j)\big]^2 \\ \quad\quad\quad\quad\quad\quad = \underset{m}{\sum}\underset{n}{\sum}\big[f^2(m,n)+t^2(m-i,n-j)-2f(m,n)t(m-i,n-j)\big]^2$

$f(m,n)t(m-i,n-j)$이 constant가 아니기 때문에 focus

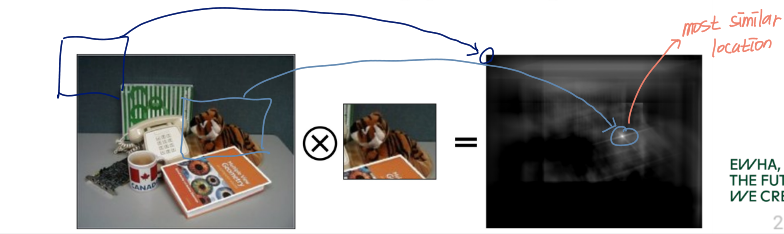
→ Maximize $R_{tf}(i,j) = \underset{m}{\sum}\underset{n}{\sum} t(m-i, n-j)f(m,n)$ → Cross-correlation

$R_{tf}=t \otimes f$일 때, $R_{tf}$의 값이 큰 게 최적의 위치라고 할 수 있는데,,,,

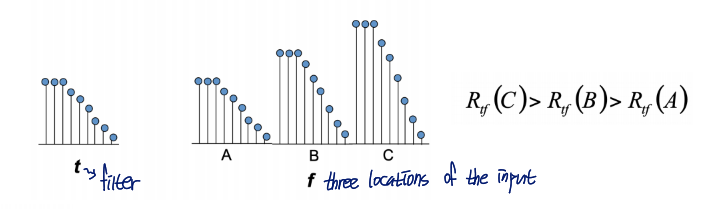
이렇게 무작정 location의 값들이 크다고 결과값이 크게 나오는 참사가 발생할 수 있음
A가 변수로 들어갔을 때 R값이 제일 크게 나와야 하는데 위에서는 그렇지 않게 나옴

→ $N_{tf}(i,j)=\frac{\underset{m}{\sum}\underset{n}{\sum}t(m-i,n-j)f(m,n)}{\big[\underset{m}{\sum}\underset{n}{\sum}t^2(m-i,n-i)\big]^{1/2}\big[\underset{m}{\sum}\underset{n}{\sum}f^2(m,n)\big]^{1/2}}$
magnitude로 나눠서 위와 같은 일이 벌어지지 않도록 함

Convolution and Cross-Correlation

• convolution과 cross-correlation은 convolution은 kernel을 flip한다는 점을 빼면 동일함
  현재는 correlation도 convolution이라고 부른다고 함(signal 관련 처리 때는 둘을 구분함)
• 많은 경우, the distiction between the two is not strictly made
  -CNN(Convolutional Neural Networkds) apply multiple cascaded convolution kernels with applications in machine vision and artificial intelligence
  • 그리고 이들은 대부분 사실상 convolution이 아닌 cross-correlation 방식을 사용함

Convolution is a Generic Function

Separable linear filter: $K=vh^T$
2D filter를 1D filter 2개로 쪼갬

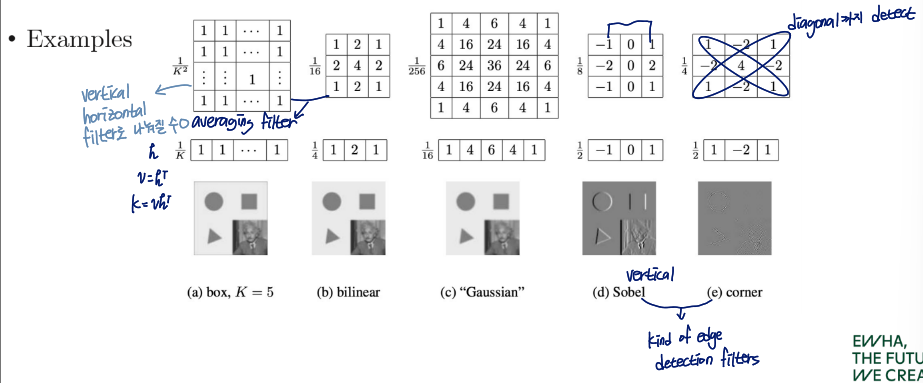
These operations can be significantly sped up by first performing a one-dimensional horizontal convolution followed by a one-dimensional vertical convolution
1차원 벡터 두 개로 쪼갬으로써 계산 속도를 높일 수 있음
$O(k^2) \rightarrow O(2k)$

Gaussian Smoothing

Gaussian kernel: $h(i,j)=\frac{1}{2\pi\sigma^2}e^{-\frac{1}{2}(\frac{i^2+j^2}{\sigma^2})}$

$\rightarrow g(i,j) = \frac{1}{2\pi\sigma^2} \underset{m=1}{\sum}\underset{n=1}{\sum}{e^{-\frac{1}{2}(\frac{m^2+n^2}{\sigma^2})}f(i-m,j-n)}$

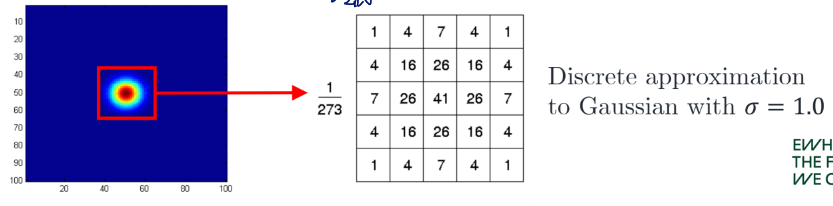
2D Gaussian is separable

$g(i,j) = \frac{1}{2\pi\sigma^2} \underset{m=1}{\sum}\underset{n=1}{\sum}{e^{-\frac{1}{2}(\frac{i^2+j^2}{\sigma^2})}f(i-m,j-n)} \\ \quad\quad\quad =\frac{1}{2\pi\sigma^2} \underset{m=1}{\sum} e^{-\frac{1}{2}\frac{m^2}{\sigma^2}} \underset{n=1}{\sum} e^{-\frac{1}{2}\frac{n^2}{\sigma^2}}f(i-m,j-n)$ → Use two 1D Gaussian filters

Repeated averaging ≒ Gaussian smoothing

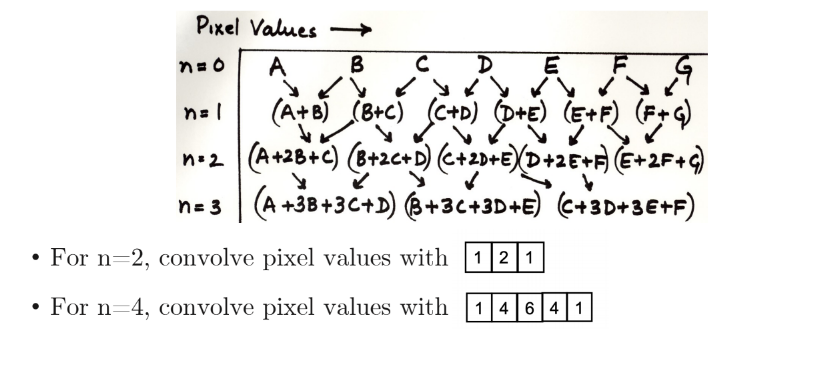
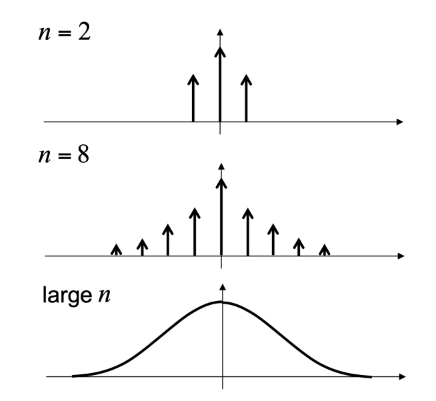
가우시안 필터는 $\sigma$의 값이 커질수록 smoothing effect가 강해짐

그리고 가우시안 스무딩은 사람이 초점을 잘 못 맞춰서 볼 때랑 유사한 결과를 만들어냄

이런 그림에 가우시안 필터를 취하면

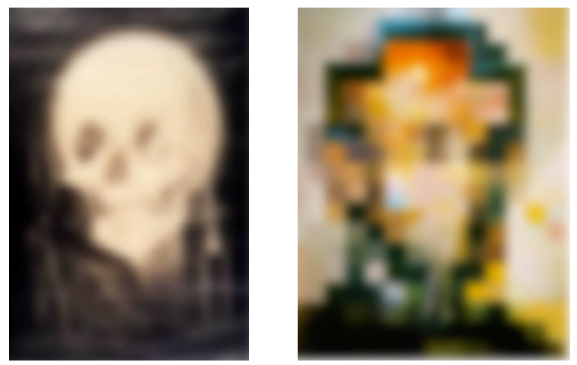
이렇게 사람이 그림을 흐릿하게 볼 때와 같은 효과를 줌

Median Filter

은 평균값을 통한 Smoothing의 경우

• edge가 blur해짐
• outliers에 민감함
  
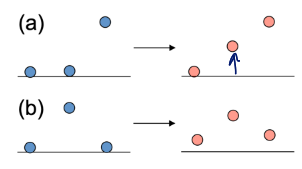
  (a): blurs edges, (b): sensitive to outliers

가우시안 스무딩은 average smoothing보다 더 자연스러운 결과를 내보임

Median filtering

• 픽셀 주변의 $k^2$ values 정렬
• 중앙값 선택
  
• Non-linear하기 때문에 convolution으로 구현 불가능함

Gaussian vs. Median Filter

gaussian noise와 salt-and-pepper noise

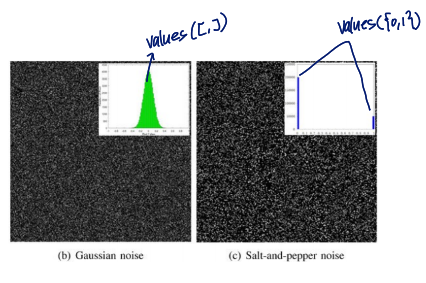
Salt and pepper noise

salt and pepper noise는 outlier가 심함
→ outlier에 robust한 median filter의 성능이 더 좋음

Gaussian noise

Gaussian filter의 성능이 더 좋음

⇒ 이미지의 특징에 따라 smoothing의 기법이 적절한 방법을 골라서 적용해야 함