Convolution 연산 이해하기
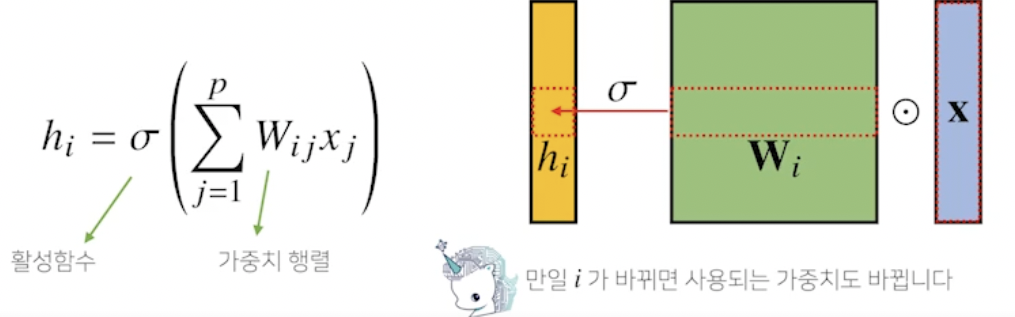
- 지금까지 배운 MLP 는 각 뉴런들이 선형모델과 활성함수로 모두 연결된 (fully-connected) 구조였음
→ 가중치 행렬 사이즈와 파라미터 수가 큼
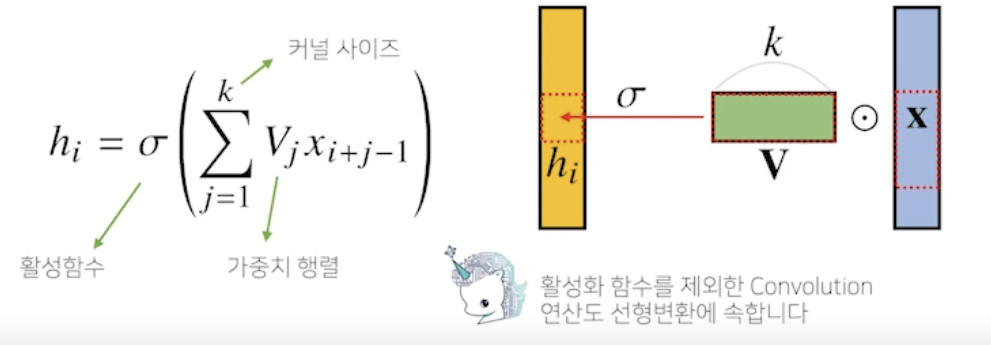
- Convolution 연산은 커널 (kernel) 을 입력벡터 상에서 움직여가면서 선형모델과 합성함수가 적용되는 구조
- V : 커널, k : 커널 사이즈
- 입력벡터 x 를 모두 활용하는게 아니라 k 만큼 추출하여 사용
- 커널은 그대로 두고 커널 사이즈만큼 x 상에서 이동하면서 계산
- i 가 바뀌면 활성화 함수랑 convolution 말고 x 가 움직이며 연산
→ 가중치 행렬이 i 에 따라 바뀌는게 아니라 고정된 v 는 움직여가며 연산되는게 차이점 - convolution 연산도 선형변환의 한 종류
- 커널 사이즈는 i 에 관계없고 j 에만 관련 → 파라미터 사이즈 줄어들었음
- 수학적 의미
- 신호 (signal) 를 커널을 이용해 국소적으로 증폭 또는 감소시켜서 정보를 추출 또는 필터링하는 것

- f 와 g 는 신호 또는 커널임. 파라미터로 x-z 나 i-a 있는게 신호. z 나 a 있는게 커널
- 엄밀한 식은 위의 사진처럼 - 가 아니라 + 를 사용함, 전체적으로는 + 냐 - 냐 (convolution 이냐 cross-correlation 이나 큰 차이없음, 하지만 컴퓨터에서는 중요함) → + 사용 (cross-correlation), 역사적으로 convolution 이라 불러서 그렇게 부름
- 커널은 정의역 내에서 움직여도 변하지 않고 (translation invariant) 주어진 신호에 국소적 (local) 으로 적용됨
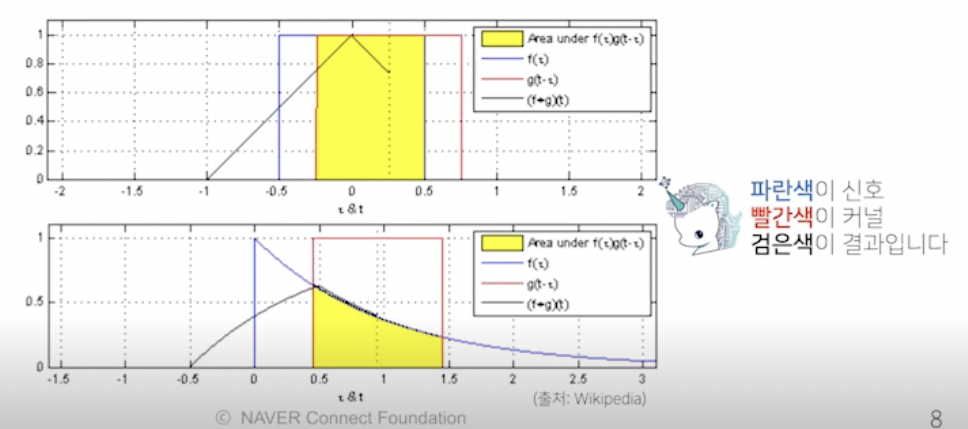
- 빨간색 커널을 움직여서 파란색 신호와 노란색 (국소적) 연산을 통해 검은색 결과가 나옴
→ 시그널 (파랑) 을 커널을 통해 바꾸는 작업
영상처리에서 Convolution
- 여러가지 커널 (흐리게, 맑게 등) 을 통해 원하는대로 영상을 추출함
다양한 차원에서의 Convolution
- Convolution 연산은 1차원뿐만 아니라 다양한 차원에서 계산 가능
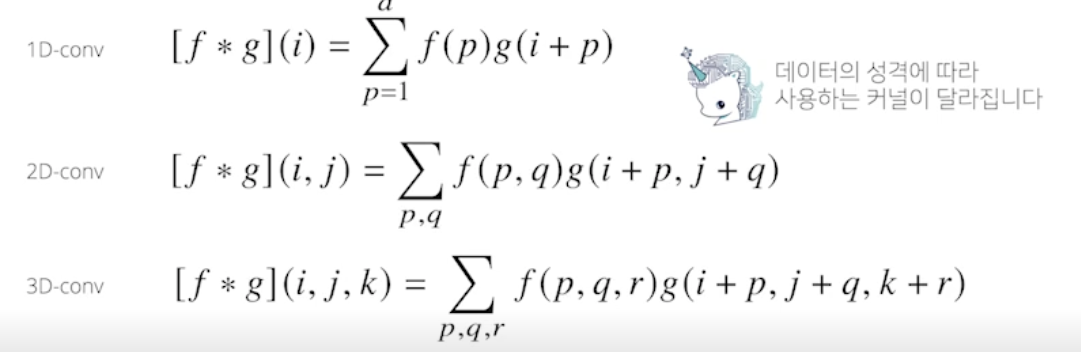
- 차원이 높아져서 i, j, k 가 바껴도 커널 f 의 값은 바뀌지 않음
2 차원 Convolution 연산 이해하기
- 매우 많이 활용되므로 잘 볼 것
- 2 차원 커널, 행렬 모양의 커널 사용
→ 이 커널을 입력벡터 상에서 가로로 세로로 움직이면서 연산 - 마지막에 합성함수 적용
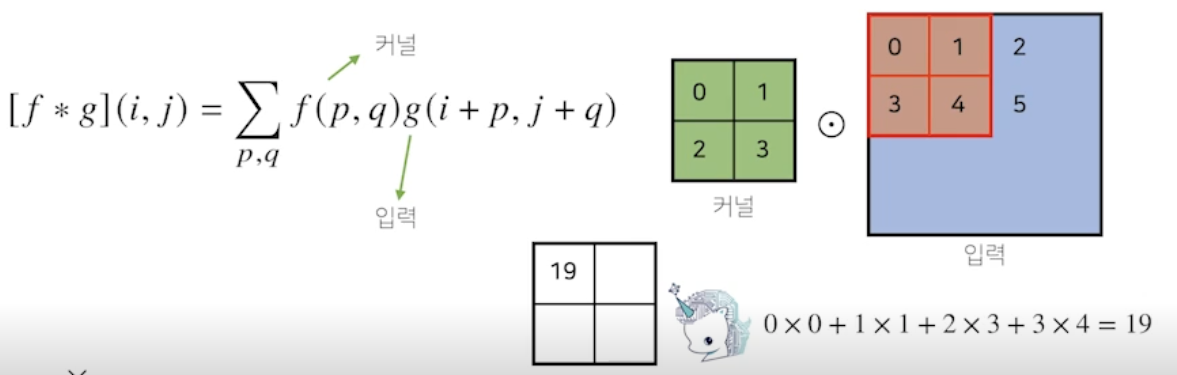
- 입력 크기를 (H, W), 커널 크기를 (), 출력 크기를 () 라 하면 출력 크기는 다음과 같이 계산

- 채널이 여러개인 2 차원 입력의 경우 2 차원 Convolution 을 채널 개수만큼 적용 (RGB 데이터가 들어오면 2차원 3개 사용, 입력은 3차원 행렬 (텐서), 커널도 3차원 행렬 (텐서)). 텐서를 직육면체 블록으로 이해하면 좀 더 이해하기 쉬움
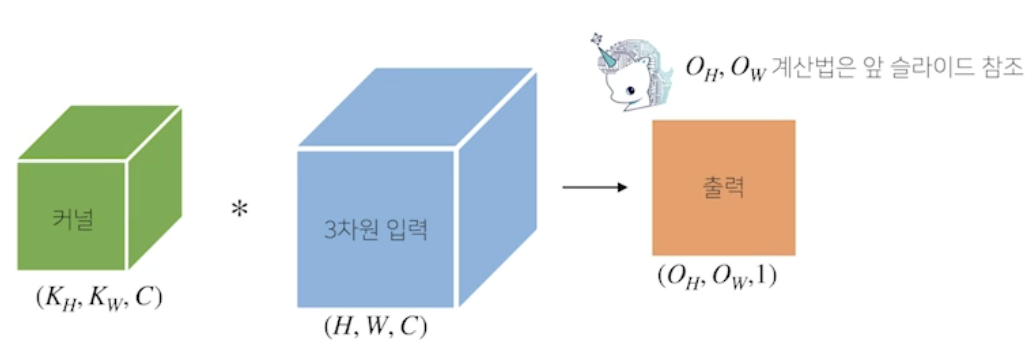
- 커널을 $O_C$ 개 만큼 사용하면 출력도 $O_C$ 텐서로 나옴Convolution 연산의 역전파 이해하기
- Convolution 연산은 커널이 모든 입력데이터에 공통으로 적용되기 때문에 역전파를 계산할 때도 convolution 연산이 나옴


- 역전파 그림
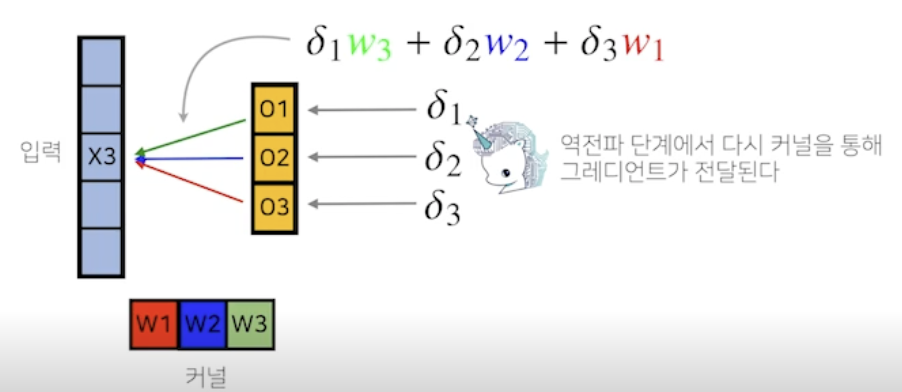

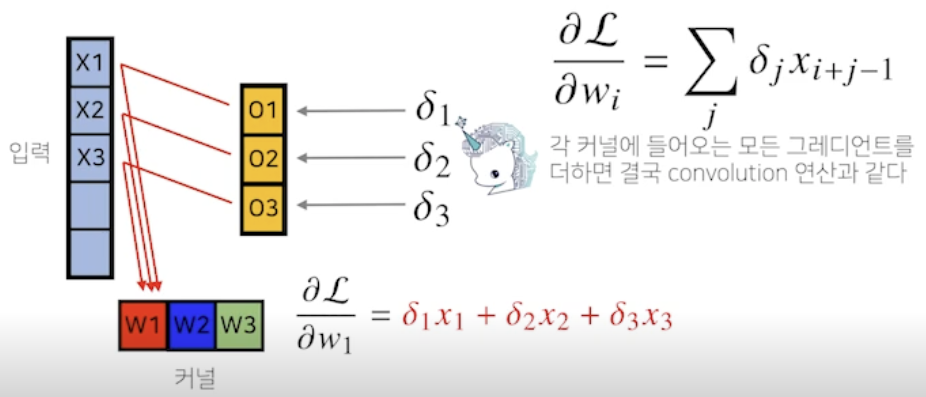
Convolution
-
수식
-
연속형
-
이산형
)
-
-
convolution 은 f 와 g 함수를 잘 섞어주는 방법
-
필터로 입력값을 도장찍듯 아웃풋을 만들며 이동함
-
2D convolution 의 의미 : 2D 이미지를 여러 필터들이 찍어내면서 필터들은 초기 웨이트에 의해 특정 기능을 하는 필터가 됨
-
32x32x3 이미지에 5x5x3 필터 4개를 찍어내면 28x28x4 아웃풋이 나옴
-
convolution 과정을 여러번 수행
-
CNN 은 convolution layer, pooling layer, and fully connected layer 로 구성됨
- Convolution and pooling layers : feature extraction
- Fully connected layer : decision making (e.g., classification)
- 최근에는 fully connected layer 를 없애는 추세, 학습시키고자 하는 모델의 파라미터 숫자가 늘어날수록 학습이 어렵고 generalization 성능이 떨어지기 때문
- convolution 은 딥하게, 파라미터는 줄이도록 진행함
*유명한 모델들의 파라미터 표를 보고 코드를 보면서 파라미터 수가 일치하는지 확인하면서 공부할 것
Stride
- 커널로 입력값을 옮기는 단위
Padding
- 커널로 입력값을 찍어내면 원래 입력값의 사이즈보다 작게 나옴
- 제로 패딩, 입력 가장자리에 0 을 채워넣어 원래 사이즈대로 나올 수 있게 해줌
- 원래 사이즈대로 나오면 입력값의 가장자리를 관찰하기 좋음
출력값 크기
- W, H (가로, 세로) 에 똑같이 적용
- n : 입력값의 가로 혹은 세로 길이, f : 필터의 가로 혹은 세로 길이
- (n - f + 2*padding)/stride + 1
파라미터 개수

- 커널의 크기 : 3x3x128
- 이 커널이 64개 존재 ⇒ 3x3x128x64 = 73,728
알렉스넷 파라미터 개수
- convolution 과정에서는 필터크기 아웃풋 뎁스 개수
- 마지막 dense layer (fully connected) 에서는 입력값 전체 크기 전체 아웃풋크기
→ 13 13 128 2 x 2048 * 2 ~ 177M, 컨볼루션에 사용되는 파라미터보다 훨씬 많은 파라미터 사용됨
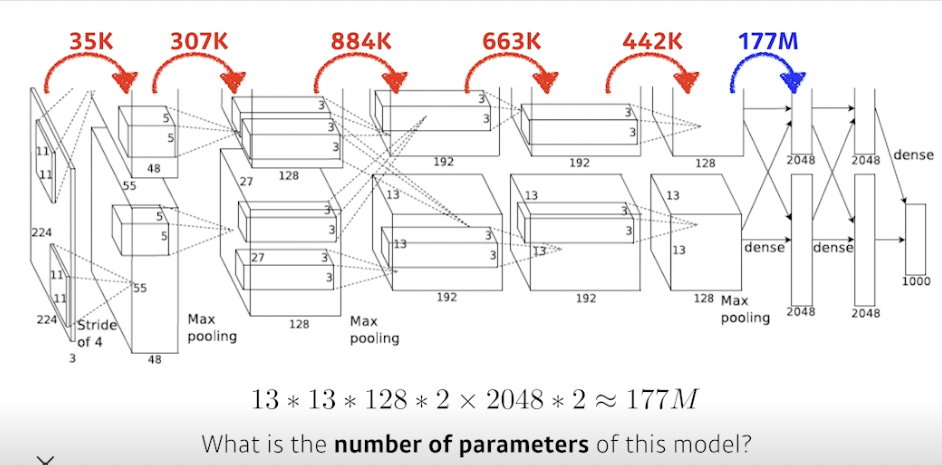
- 컨볼루션은 입력값 모든 부분에 동일한 크기로 적용하기 때문에 파라미터 개수가 적음 → 파라미터가 줄었으니 성능이 좋음
1x1 Convolution 중요
- 영역을 보지 않고 이미지에서 한 픽셀만 봄 + 채널 개수 줄임
- 왜할까?
- Dimension reduction (채널을 줄임)
- 컨볼루션 레이어를 더 깊게 쌓으면서 파라미터를 줄일 수 있음
- e.g., bottleneck architecture

참조
BoostCamp AI Tech
