What I can not create, I do not understand. - 리처드 파인만 -
Introduction
-
generative model 을 배운다는 것은 어떤걸 의미할까?
- 그럴듯한 이미지나 문장을 만드는 것 이상
- 만들어내는게 전부가 아님
-
만약 강아지 이미지들이 주어진다면?
-
Generation : 만약 를 샘플링하면 는 강아지처럼 보일 것임 (sampling)
→ implicit model
-
Density estimation : p(x) 는 어떤 이미지가 주어졌을 때, 강아지같은지 고양이같은지 구분, 즉 만들어내는거 이상으로 감지 까지 가능함 (anomaly detection)
→ 이렇게 확률까지 얻어내는 모델을 explicit 모델이라 함 -
Unsupervised representation learning : 여러 이미지들이 귀, 꼬리들과 같은 공통점이 있다는 것을 우리는 학습할 수 있음 (feature learning)
-
-
p(x) 를 어떻게 만들까?
기본 이항 분포
- 베르누이 분포 : 동전 던지기
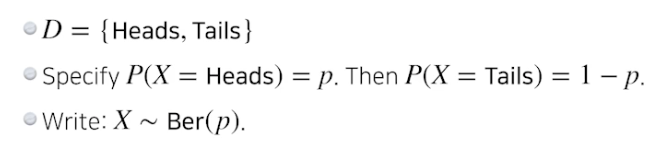
- 카테고리컬 분포 : m 면체 주사위 던지기
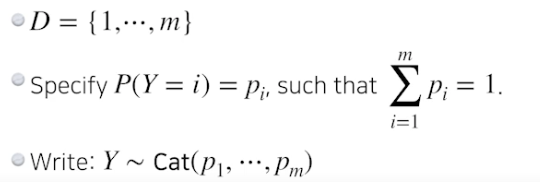
-
RGB joint distribution (결합 분포) 을 모델링한다면
- (r, g, b) ~ p(R, G, B)
- Number of cases? → 256 x 256 x 256
- 파라미터 숫자가 얼마나 필요한가? → 255 x 255 x 255 (너무 많음)
⇒ fully dependent 는 너무 많은 파라미터 필요
-
흑백 이미지 N 개 X1, ..., XN 이 있다면
-
경우의 수 → 2 x 2 ... x 2 =
-
p(x1, ..., xn) 의 파라미터 수는 → n
-
엔트리는 n 으로 설명 가능함. 하지만 이 독립 추정은 모델이 사용할만한 분포로서는 너무 강함
-
각각의 픽셀에 대해 파라미터 1 개 필요. n 개가 모두 독립적이므로 다 더하면 n 개.
⇒ fully independent 는 파라미터는 적지만 말이 안되는 추정
(Q. 지수가 배수되는 과정 더 알아봐야 함 → 독립이면 다 따로 각각 생각해서 변수 개수는 n 개, 다 더하면됨)
-
-
-
Conditional Independence
- 위 두 개의 중간 : 체인 룰과 컨디셔널을 이용해서
- 세 가지 기본적인 룰

- 체인룰을 사용하면, joint 분포를 conditional 분포로 바꿔줌
- 어떤 것도 바뀌지 않음 → fully dependent 모델 파라미터 수와 같음
- 파라미터 수
- p(x1) : 1 param
- p(x2 | x1) : 2 params (one per p(x2 | x1 = 0) and one per p(x2 | x1 = 1))
- p(x3 | x1, x2) : 4 params
- 를 따름
- Markov assumtion, 바로 전 입력에 의해 현재 입력 영향
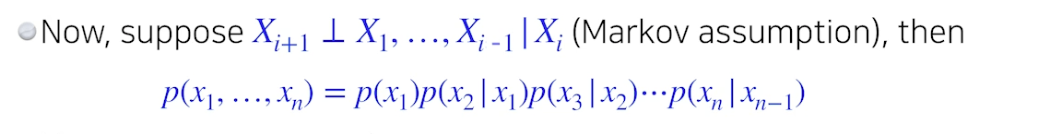
- 파라미터 수 : 2n - 1
- Markov asuumtion 모델을 레버리징하여 파라미터에 대해 exponential reduction (지수를 배수로 줄임) 가능
- Auto-regressive models 는 이 conditional independency 를 레버리징함.
Auto-regressive Model
- MNIST 이미지 28x28 짜리 숫자 사진이 있다고 가정하자.
- 우리의 목표는 p(x) = p(x1, ..., p784) 를 학습하는것, x 는 0 or 1
- 어떻게 p(x) 를 파라미터화 할까?
- joint distribution 에 체인룰 적용
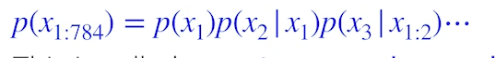
⇒ auto-regressive model
- 자기 회귀 모델은 하나의 정보가 이전 정보들에 의존적인 것
- 마코비언처럼 하나의 정보가 이전 정보에만 의존해도 (AROne 모델)
- 하나의 정보가 모든 이전 정보에 의존 (ARN 모델)
- 어떤 이미지를 자기회귀 하려면 랜덤 변수들에 대해 ordering (순서 매기기) 필요함
- 순서 매기는 방법에 따라 성능이 달라질 수 있음 (지그재그, 연속 등)
- joint distribution 에 대해 마코비언 추정을 하거나 다른 conditional independence 추정을 하는 것이 체인룰 입장에서 joint distribution 을 쪼개는 데에 어떤 관계가 있는지 생각할 것
NADE : Neural Autoregressive Density Estimator
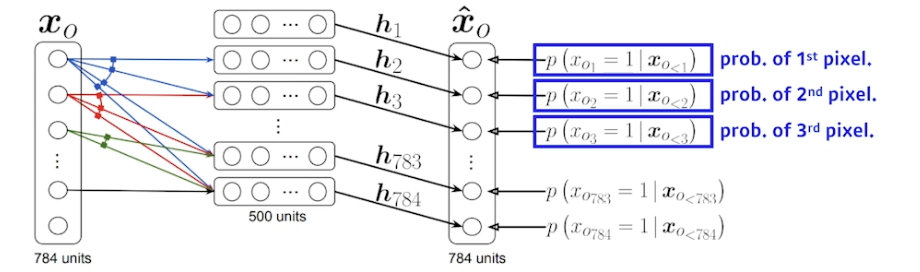
- i 번째 픽셀을 1 ~ i-1 번째 픽셀에 의존하게 만듦
- 첫 번째 픽셀의 확률분포는 독립적으로 만들고, 두 번째 픽셀의 확률은 첫 번째 픽셀에 의존 (h 가 됨), 세 번째 픽셀의 확률은 첫 번째와 두번째에 의존 ... 끝까지 진행
- 100번째 뉴럴 네트워크 (100번째 픽셀에 대한 확률분포) 만들 때는 99 개의 이전 입력들을 받을 수 있는 뉴럴 네트워크 필요
- NADE 는 explicit 모델 (생성 + 확률계산) → 주어진 입력에 대해 density 계산 가능
- 784 개의 바이너리 픽셀 {x1, ..., x784} 이 있다면, joint 확률은 아래와 같음

- 연속 확률 변수일 때는 마지막 모델에 가우시안 믹스쳐 모델을 사용
Pixel RNN
- auto-regressive model 정의하는데 RNN 사용 가능
- n x n RGB 이미지가 있을 때, R 먼저 만들고 G 만들고 B 만듦
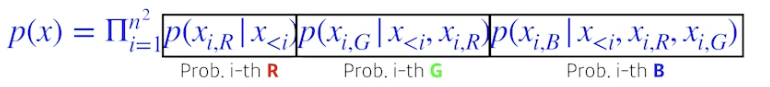
- ordering 을 어떻게 하냐에 따라 두 버전 존재
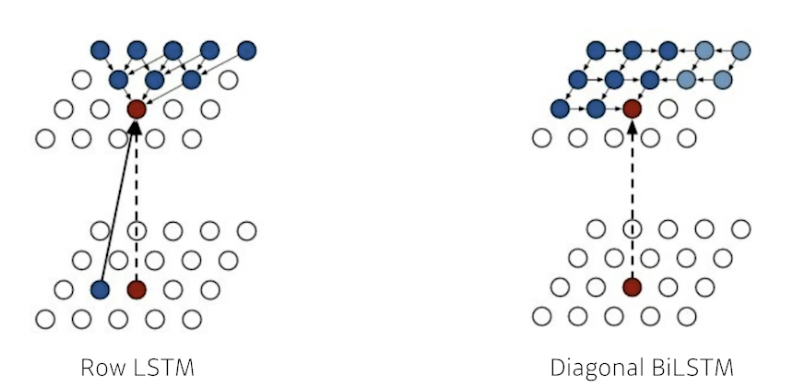
- Row LSTM : i 번째 픽셀을 만들 때 위쪽 정보 사용 (아래로 진행, 맞나?)
- Diagonal BiLSTM : bidirectional 하면서 자기 이전 정보 모두 사용 (옆으로 진행)
Latent Variable Models
- Kingma 박사가 만듦 (Adam 도 만듦, 박사 논문 읽어보는거 추천)
- Auto-encoder 도 generative model 일까? 사실 그렇지 않음, Variational Auto-encoder 가 일반 Auto-encoder 와 어떤 차이가 있고 어떻게 Variational Auto-encoder 는 generative model 되는지 알 것
Variational Auto-encoder
- Variational inference (VI)
- VI 의 목적은 variational distribution 을 posterior dist 와 최적의 매치가 되도록 최적화하는 것
- Posterior dist :
- 관측이 주어졌을 때 관심있는 확률 변수의 확률 분포
- 계산하기 힘듦 → 근사하는게 vd
- Variational dist :
- 가장 관심있는 pd 를 근사한 것
- Posterior dist :
- KL 발산을 사용해서 true posterior 를 최소화하는 vd 찾고자 함
- VI 의 목적은 variational distribution 을 posterior dist 와 최적의 매치가 되도록 최적화하는 것
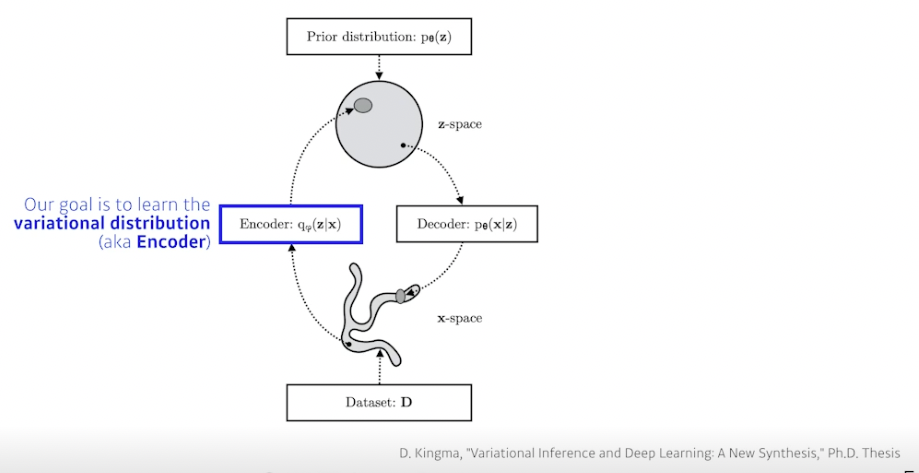
-
VD 를 찾는게 목적 (Encoder)
-
문제는 posterior 를 모르는데 어떻게 이를 근사하는 VD 를 만들 수 있을까?
→ ELBO 트릭 사용
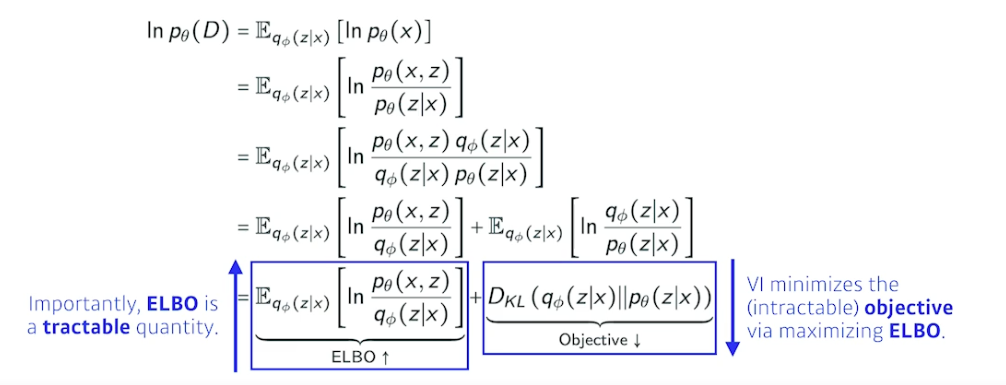
- ELBO (Evidence Lower Bound) 를 키움으로써 거리를 줄여줌
- 수식 따라가보는거 추천
- ELBO
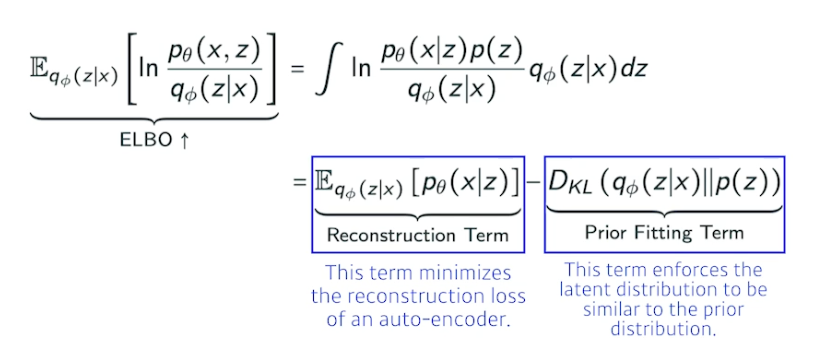
-
Reconstruction Term : 인코더를 통해 x 라는 입력을 latent space 로 보냈다가 디코더로 돌아오는 Reconstruction loss 를 줄이는 것
-
Prior Fitting Term : x 라는 이미지들을 latent space 에 올림 (점들). 점들이 이루는 분포가 내가 가정하는 latent space 의 prior dist (사전 분포) 와 동시에 만족하는 것과 같음
- 엄밀한 의미에서 Implicit model⇒ 어떤 입력을 latent space 로 보내서 무언가를 찾고 이를 다시 reconstruction 하는 term 만들어지고, generative model 이 되기 위해서는 latent space 된 prior dist 로 z 를 샘플링 하고 디코더를 태워서 나온 아웃풋 (이미지) 를 제너레이션 result 로 봄.
-
일반 auto encoder 는 인풋이 latent space 갔다가 output 나오므로 generation model 아님
-
Key Limitation
- intractable 모델 (가능성 측정이 힘들다)
- VA 는 Explicit 모델이 아님, 어떤 입력이 주어졌을 때 얘가 얼마나 비슷한지 (likeli 한지) 알기 어려움
- prior fitting term 은 반드시 미분가능, 따라서 diverse latent prior dist 사용하기 힘듦
- 일반적으로 isotropic 가우시안 사용 (모든 아웃풋 차원이 독립)
- intractable 모델 (가능성 측정이 힘들다)
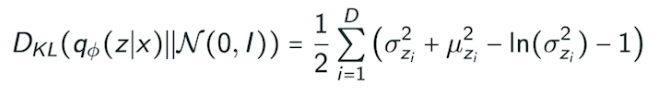
- 어떤 prior dist 가 가우시안이면, variation dist 와 prior dist 사이의 KL 발산은 위와 같이 close form 으로 나옴
- 가장 큰 단점 : 인코더 활용할 때 prior fitting term 이 KL 발산을 활용하는 것, 가우시안 아닌 경우 활용 힘듦
Adversarial Auto-encoder, AAE
- Gan 을 활용해서 latent dist 사이의 분포를 맞춰줌
- Auto encoder 의 KL 발산에 있는 prior fitting term 을 GAN objective 로 바꾼 것
- 샘플링 가능한 latent dist 가 있으면 맞춰줄 수 있음 (uniform dist, 가우시안 믹스쳐 등) → 여러 분포 활용 가능하다는게 장점
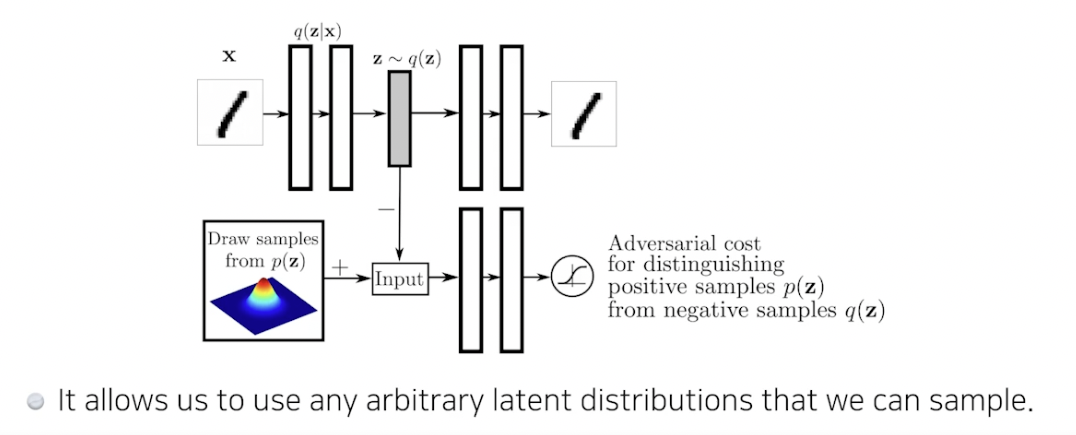
- 성능도 VA 보다 좋을 때가 많음
GAN
-
아이디어 : 도둑 (Generator) 이 위조지폐를 만드는데 이를 잘 분별하는 경찰 (Discriminator) 이 있다. 도둑은 분별된 돈으로 더 진짜같이 만들려하고, 경찰은 위조와 진짜지폐를 봐서 더 잘 구분하려함
→ 반복함으로써 generator 성능을 높임
-
two-player game
- 한 쪽은 높이고 싶어하고, 한 쪽은 낮추고 싶어함
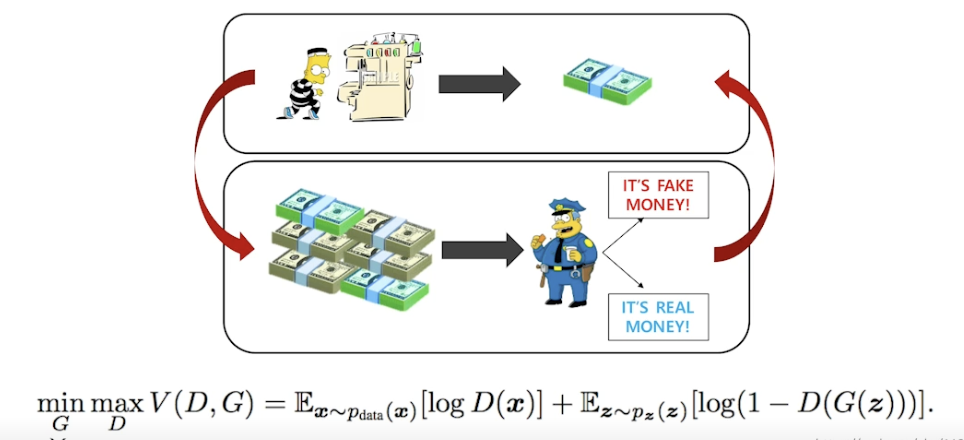
- 장점 : discriminator 가 성능이 좋아짐에 따라 generator 가 좋아진다.
- Implicit model
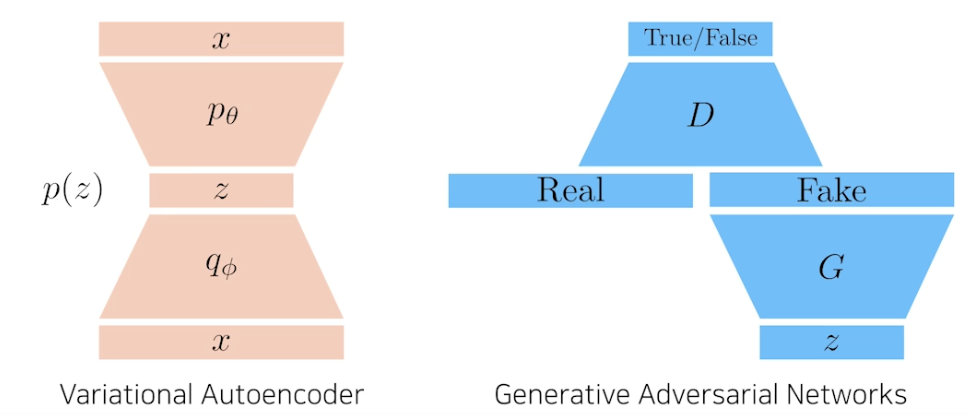
- z 로 출발해서 제너레이터 통과해서 가짜 만들고 디스크리미네이터는 가짜와 진짜를 보고 판단
- Discriminator
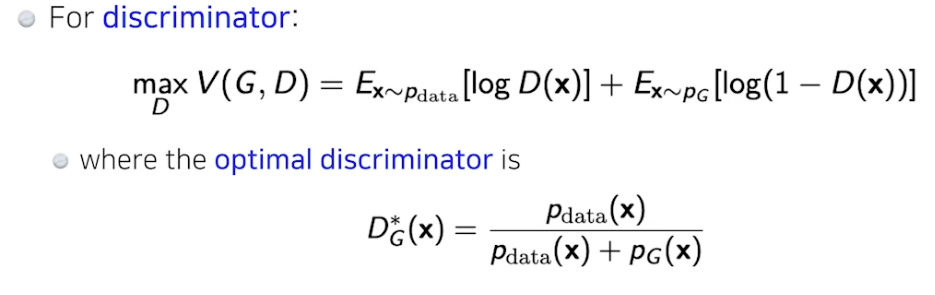
- Generator
- optimal discriminator 를 집어넣음

- 엄밀히 말하면 dis 가 optimal 이라고 가정했을 때, 이를 gen 이 학습하면 위와 같은 식이 나왔는데 실제로는 dis 가 optimal 수렴하는거 보장 힘듦 → gen 식 보장 안됨 (이론적으로는 가능하지만)
- AAE 에 활용
DCGAN
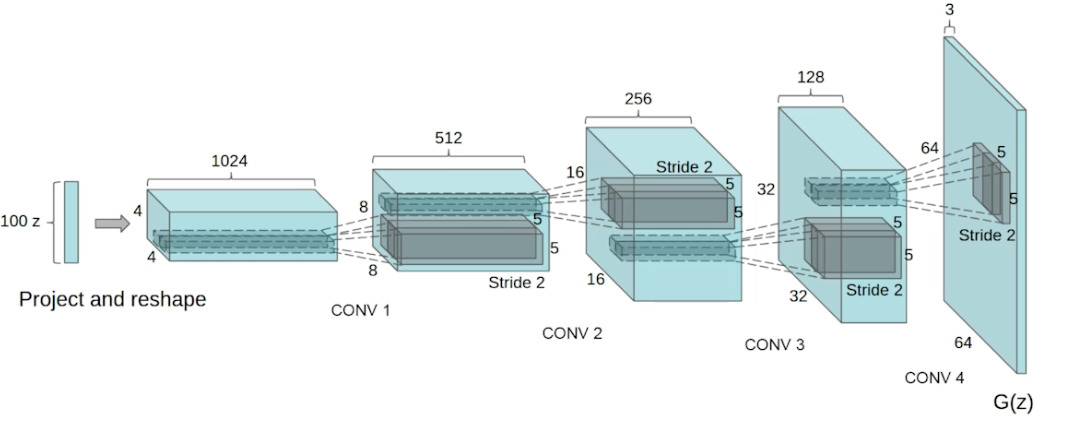
- 기본 GAN 은 MLP, 얘는 이미지에 사용
- LeakyReLU 사용
- 이미지 만들 때 좋은 하이퍼파라미터 사용
Info-GAN
- 학습할 때 단순히 z 로만 만드는게 아니라 class c 를 사용해 만들자.
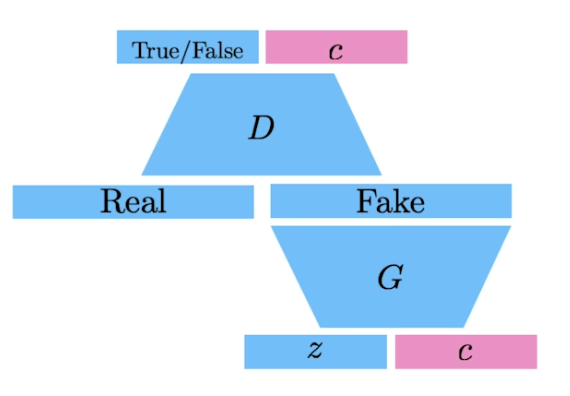
Text2Image
- 문장을 사진으로 바꿈
- DALL-E 의 조상
Puzzle-GAN
- 이미지 안에 서브패치 (헤드라이트, 바퀴 등) 들로 원래 이미지 복원하는데 사용
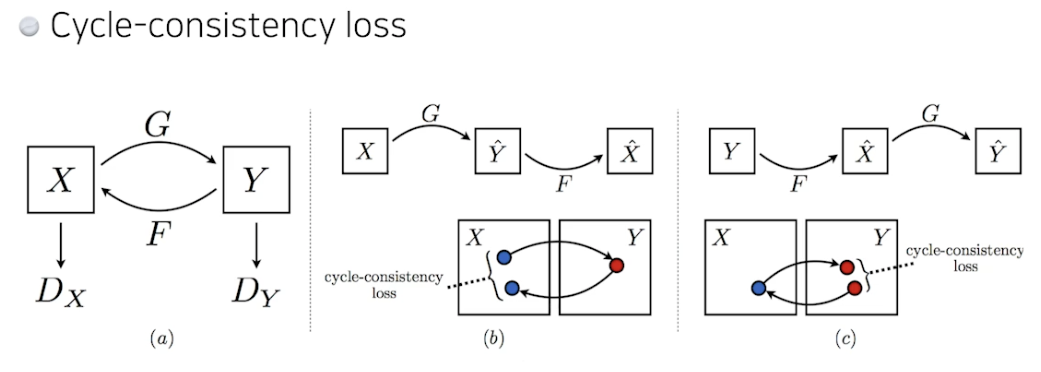
CycleGAN
- 이미지 사이 도메인 변경, 말→얼룩말 바꾸기
- Cycle-consistency loss 중요
Star-GAN
- 인풋을 어떤 필터에 따라 바꿔줌, 컨트롤 할 수 있게 해줌
- 네이버 작품
Progressive-GAN
- 센세이션한 성능
- 4x4 픽셀 → 8x8 → ... → 1024x1024 로 늘려나가면서 학습
- 좋은 성능 이미지 만들어냄
Further Reading
참조
BoostCamp AI Tech
