뉴럴 네트워크 - MLP

Neural Networks

• 동물의 뇌를 구성하는 생물학적 뉴런 네트워크에서 애매하게 영향받은 컴퓨터 시스템 (실제 인간의 뇌가 역전파가 일어나느냐? 아니라고 봄, 교수님은 실제 뇌와 비슷한 구조가 아니라고 봄)
  • 하늘을 날고 싶다고 해서 비행기가 새처럼 생길 필요는 없음 → 지능을 만들고 싶다해서 인간 뇌구조를 만들 필요는 없음
• 뉴럴 네트워크는 행렬의 연산을 하고 이것을 비선형으로 바꾸는 연산을 반복하는 함수 근사자

Linear Neural Networks

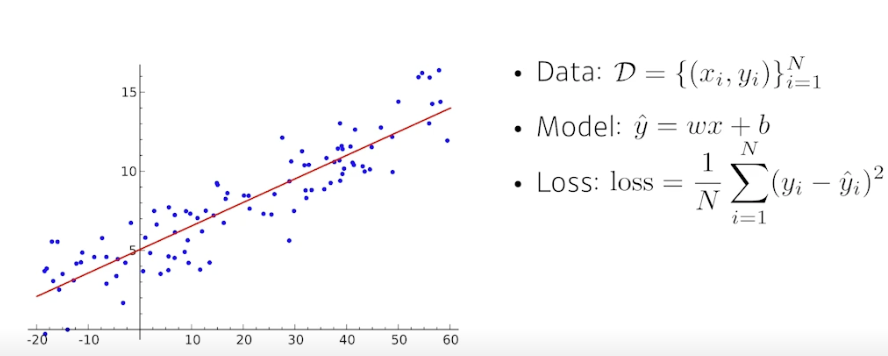
• Data : 1 차원의 x, y 데이터 1~N 개
• Model : y_hat = wx + b
• Loss : 정답과 예측값 차이의 제곱 평균
  
• 경사하강법, optimization variables 업데이트하는 방법
  • loss 를 w 에 대해 편미분하고 이를 lr 과 곱하여 현재 w 에서 뺌.
  • 마찬가지로 b 에 대해서도, loss 를 b 에 대해 편미분하고 이를 lr 과 곱하여 현재 b 에서 뺌.
  • 딥러닝에서는 마지막 층의 w 와 시작점에 대한 영향력을 알기 위해 바로 옆 레이어끼리 편미분하여 각각의 값에 경사하강법 수행

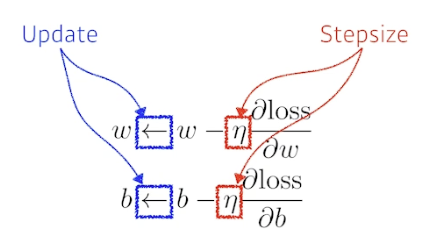
- 적절한 스텝사이즈를 잡아야 함

• 다차원의 input 과 output 이라면 행렬 연산 수행

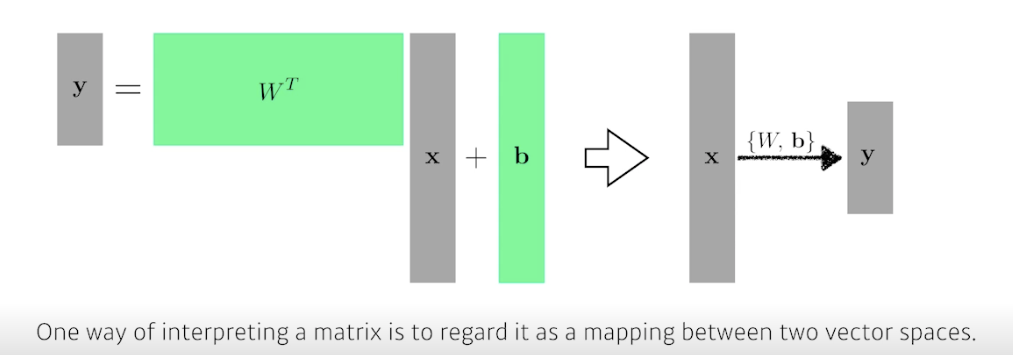
- 행렬은 두 개의 벡터 공간을 선형 변환 (연결) 해주는 것으로 이해 가능

• 딥러닝은 여기서 히든 레이어와 W 를 더 늘려 나감
  • 근데 여기서 선형 결합만 계속 반복하는건 1번의 선형결합과 다를게 없음 → 비선형함수와 결합해서 표현을 극대화한 벡터를 얻어서 다음 스텝 수행

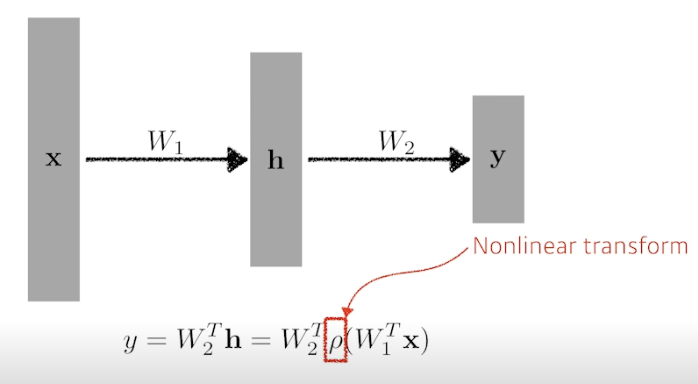
• Activation functions (비선형 함수)
  • ReLU
  • Sigmoid
  • Hyperbolic Tangent (tanh)
  • 어떤게 제일 좋을지는 문제마다, 상황마다 다름 → 하지만 딥러닝에서는 꼭 써야함

Multi-Layer Perceptron, MLP

loss functions

• 손실 함수의 목적은 우리가 예측한 값과 실제 값의 차이를 최소화 하는 것
• 꼭 제곱하는 MSE 를 사용할 필요는 없음, 절댓값을 제곱할 수도 있고, 그냥 절댓값 씌울 수도 있음
  → 아웃레이어에 대응하다가 거기에 적합한 모델이 되버릴 수도 있음
• 손실 함수가 어떤 성질을 가지고 있고, 이게 왜 내가 원하는 결과를 얻어낼 수 있는지 알아야 함
  1) 회귀 문제에서는 MSE 가 적합
  2) 분류 문제를 생각해보면, 아웃풋은 one-hot vector 가 나옴 (하나만 1이고 나머지는 0)
  → Cross-Entropy 를 사용 → 그 차원에 해당하는 값만 키워줌
  다른 말로 예측 결과 벡터가 다른 값들에 비해 그냥 높기만 하면 됨 → 이것을 수학적으로 표현해주는게 CE
  ⇒ 근데 과연 CE 가 분류 문제 푸는데 최적인가? 고민해보고 판단해봐야 함
  3) 확률적 문제 (Probabilistic Task) 에서는 MLE(최대가능도) 함수를 사용하여 적절한 모수를 추정
• 사람 얼굴을 보고 나이를 맞추는 문제에서 단순히 나이만 맞추면 회귀 문제
• 20살일 확률, 30살일 확률 등을 알려준다면 확률적 문제

참조

• BoostCamp AI Tech