양자화의 초석 : Fixed Point, Floating Point
양자화는 실수와 관련이 깊기 때문에 실수 체계에 대해 먼저 살펴보자.
Fixed Point
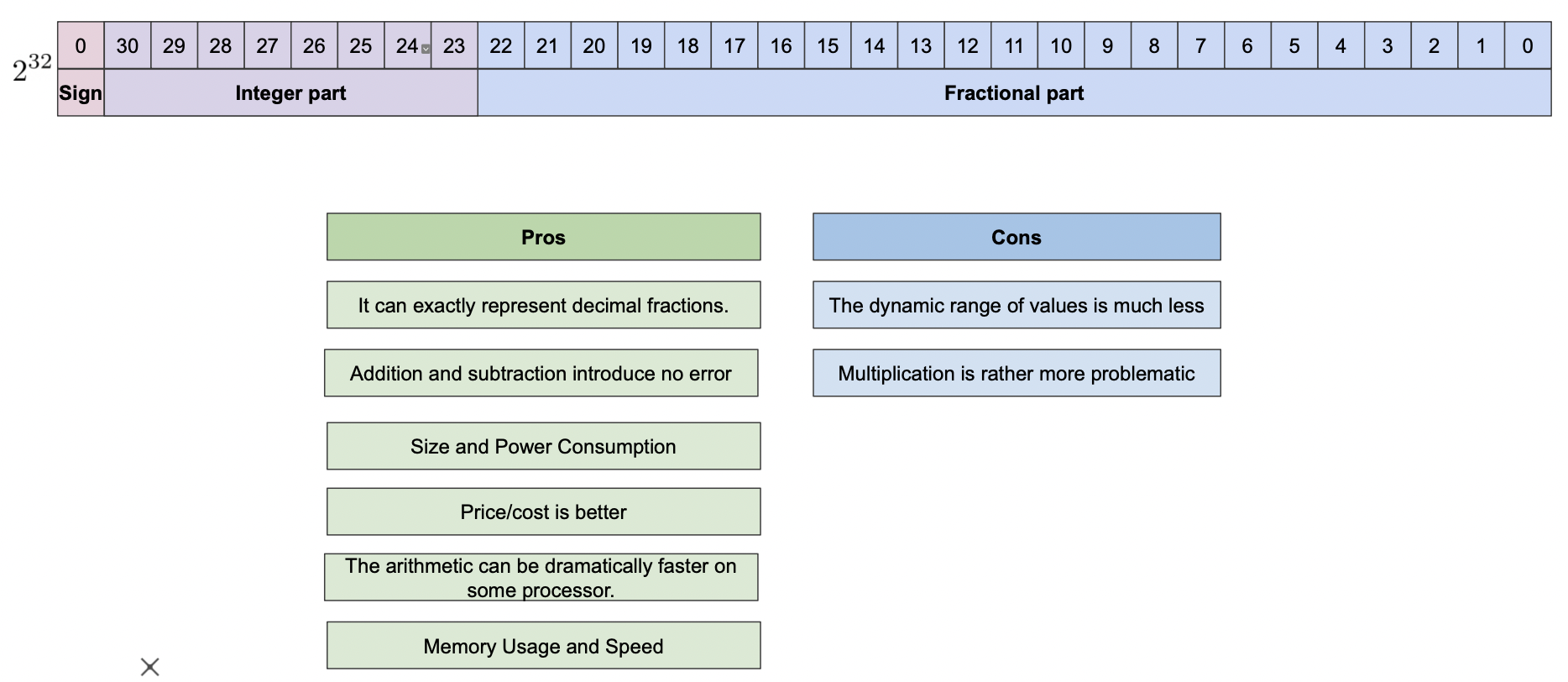
Fixed Point 는 정수부 실수부를 명확히 구분하는 방법이다.
직관적이라는 장점이 있지만 계산에 있어서 좋지 않다.
Floating Point
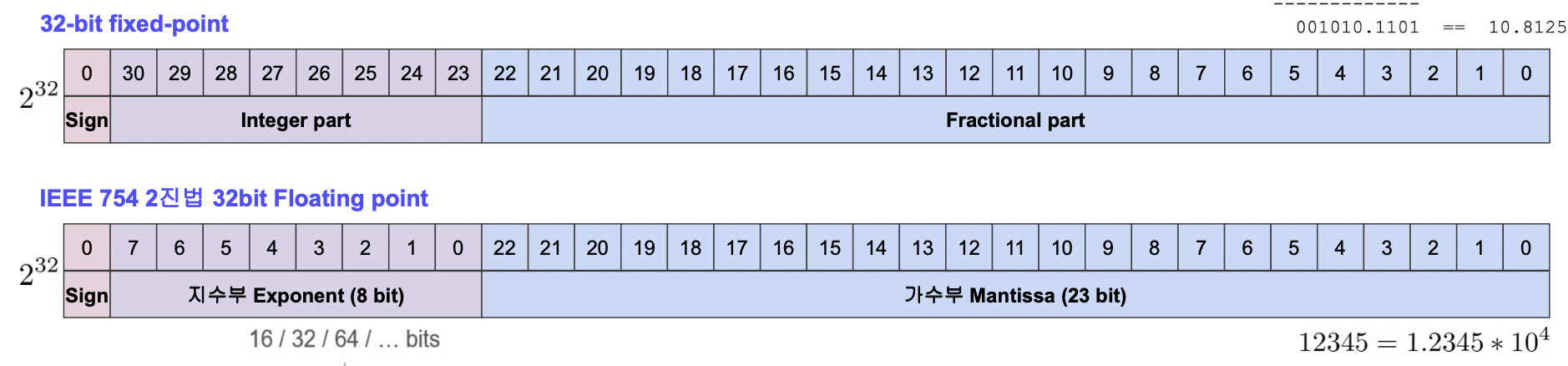
Floating Point 는 아래 그림의 두 번째 모형과 같이 지수와 가수를 통해 수를 실수를 표현한다.
Fixed Point 에 비해 지수를 올리기는 편하지만 하드웨어에서 구현은 더 힘들다.
그러나 계산이 용이하므로 Floating Point 를 많이 사용한다.
FPU (Floating Point Unit)
Floating Point 를 계산해주는 유닛으로 CPU 에 내재된 경우가 많다.
연속형 값, 이산형 값
floating number (연속형 값) 를 처리하기 위해서는 많은 코스트를 소요하는데 이를 integer (이산형 값) 으로 만들면 적은 코스트를 사용할 수 있다.
연속형 값을 이산형 값으로 바꾸는 작업이 양자화라고 볼 수 있다.

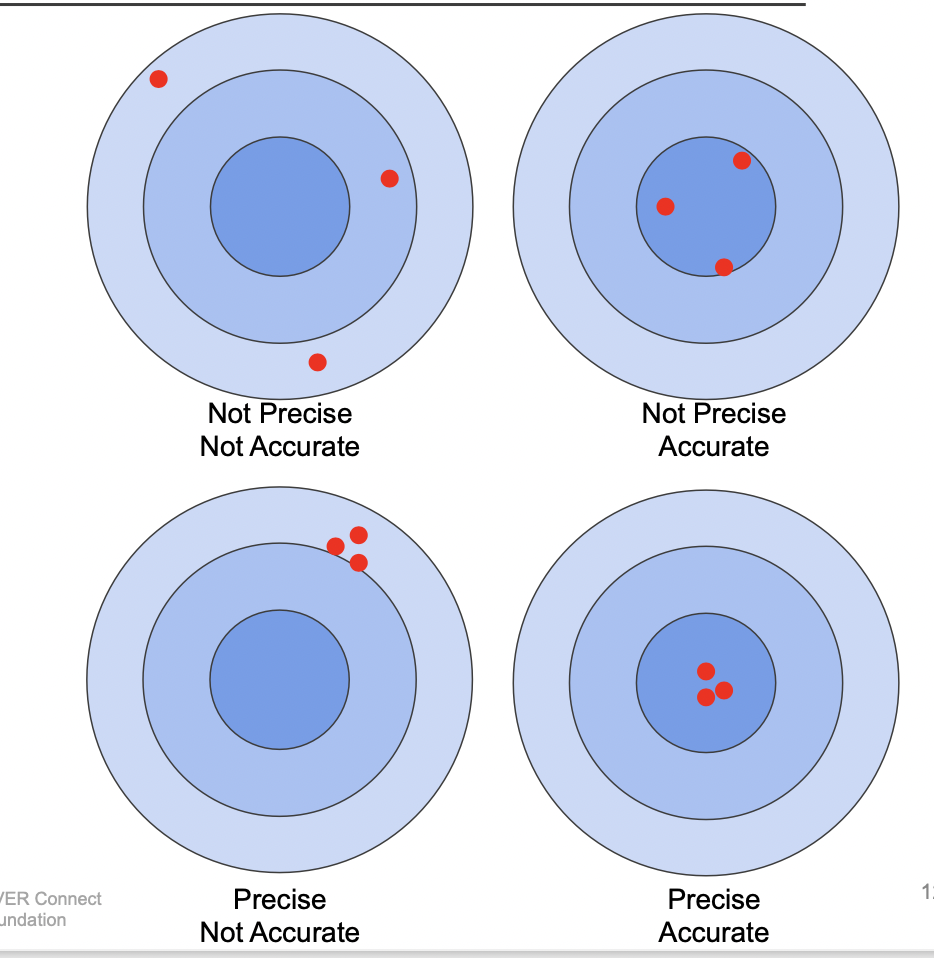
양자화의 성능 : Precision (정밀도) & Accuracy (정확도)
정밀도는 모여있는 정도 (variance 측면), 정확도는 가운데에 가까운 정도 (bias 측면) 이다.
양자화를 수행했을 때에도 정밀도와 정확도가 유지되어야 한다.
Quantization 이란
양자화, 연속된 값을 연속되지 않은 값으로 만들어 표현력은 줄어들지만 가벼워지게 만들자
특장점
- 모델 사이즈가 줄어든다.
- 요구되는 메모리 bandwidth 가 줄어든다.
- float32 with FLU 보다 int8 을 장착한 device 의 계산 속도가 빠르다.
- inference 에서 속도를 높이는 기초적인 방법이다.
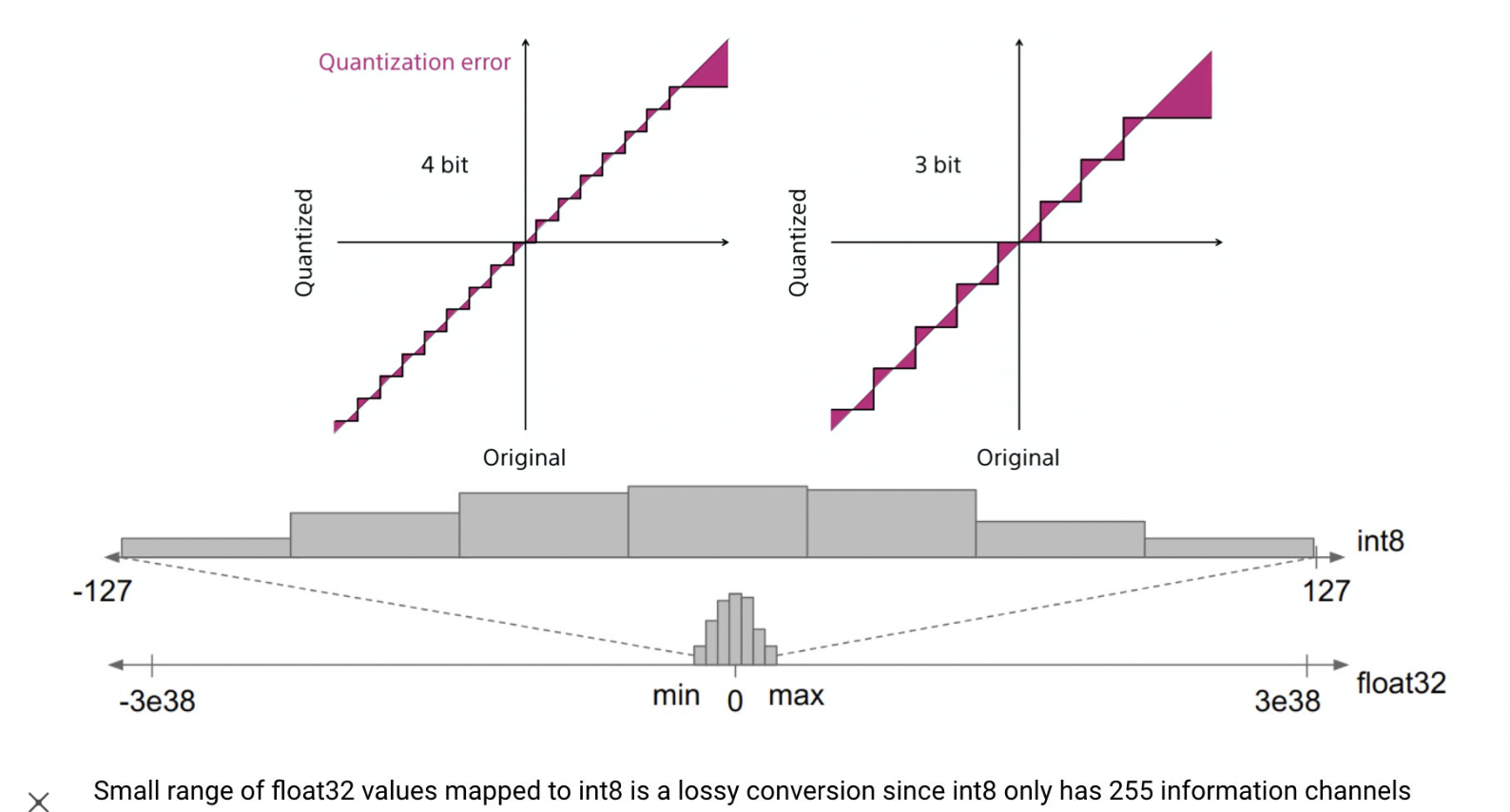
양자화와 정보 손실
세세한 표현을 못하게 되므로 정보 손실이 일어난다.
메모리는 더 많이 사용하지만 더 많은 비트로 표현을 하게 되면 정보 손실이 줄어든다.
Affine Quantization
Affine transformation 을 통해 양자화를 할 때, 원본의 비율은 그대로 유지하여 모형이 비슷하게 만들어준다.
단, 각이나 값들은 소실될 수 있다.
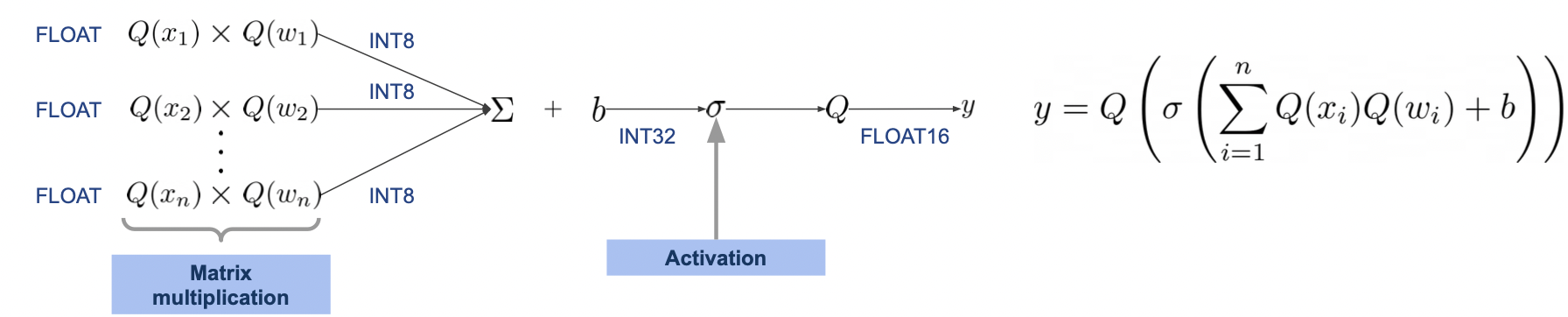
Quantizing Activation and Weight
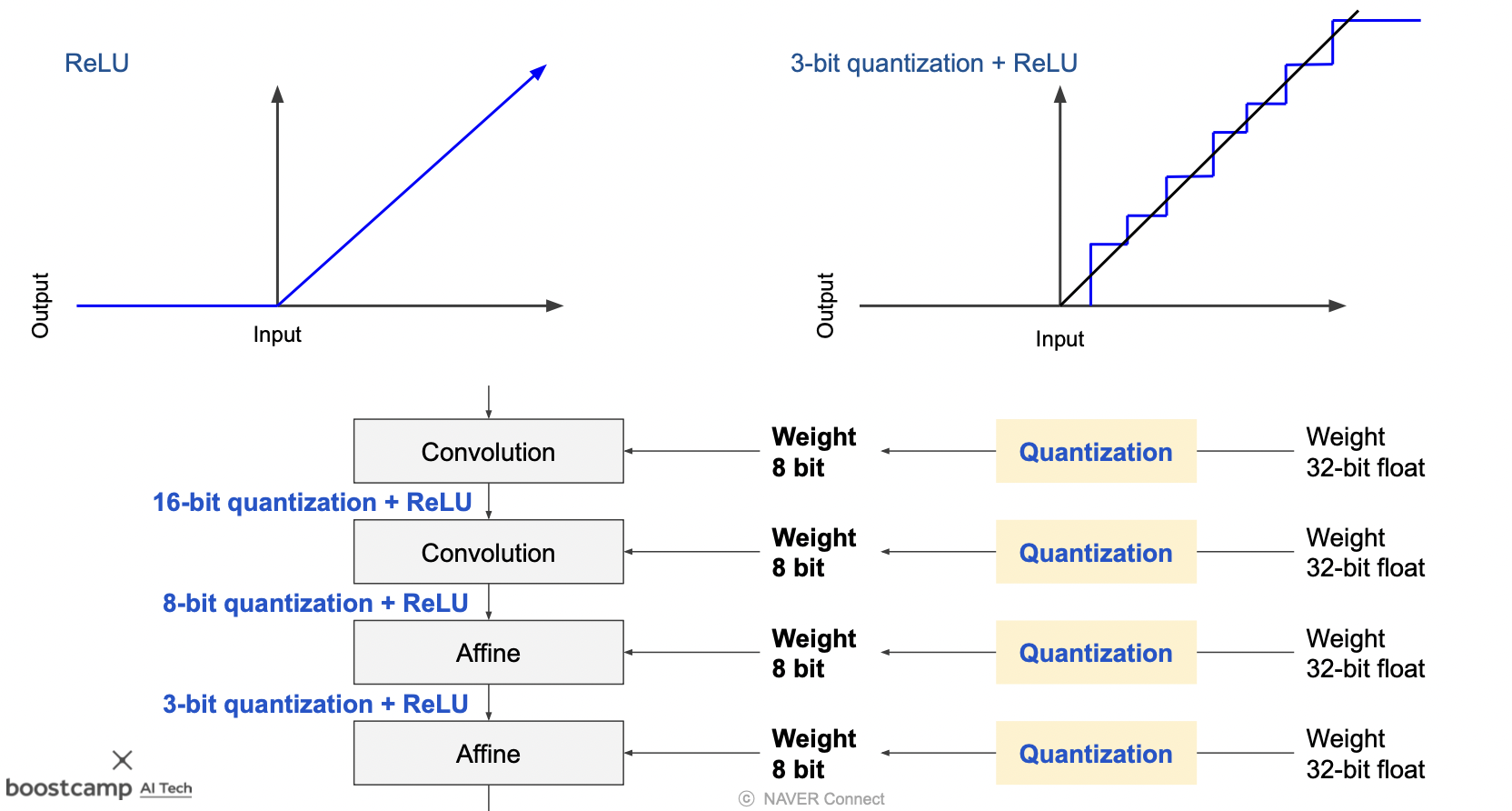
양자화된 파라미터로 학습을 진행할 때, 활성함수 또한 적은 비트의 값을 다룰 수 있게 변해야 한다.
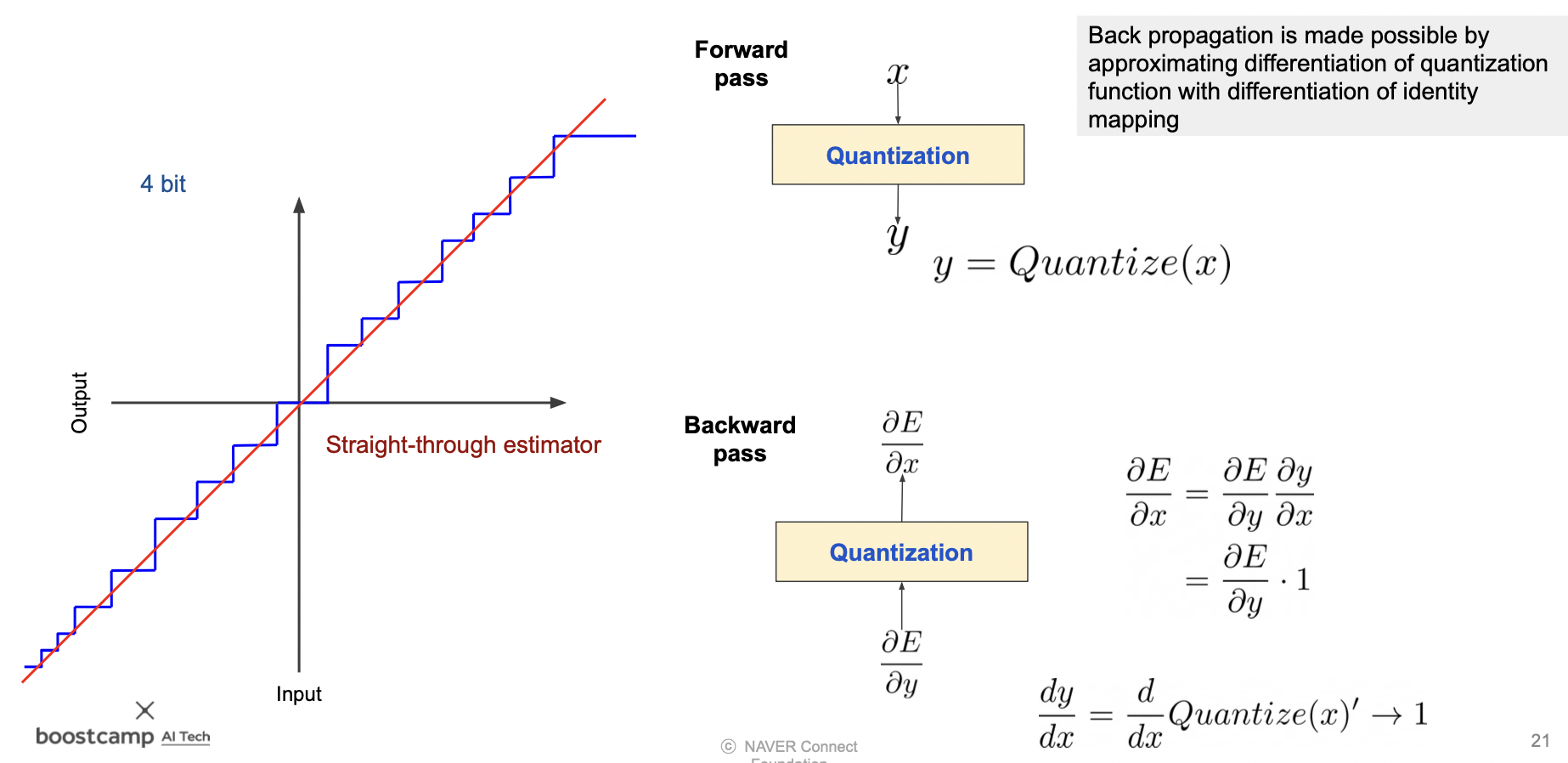
양자화의 미분
quantized 된 값을 미분할 수 없기 때문에 1 로 두기도 한다.
또는 smoothing 해서 계단형으로 사용하기도 한다.
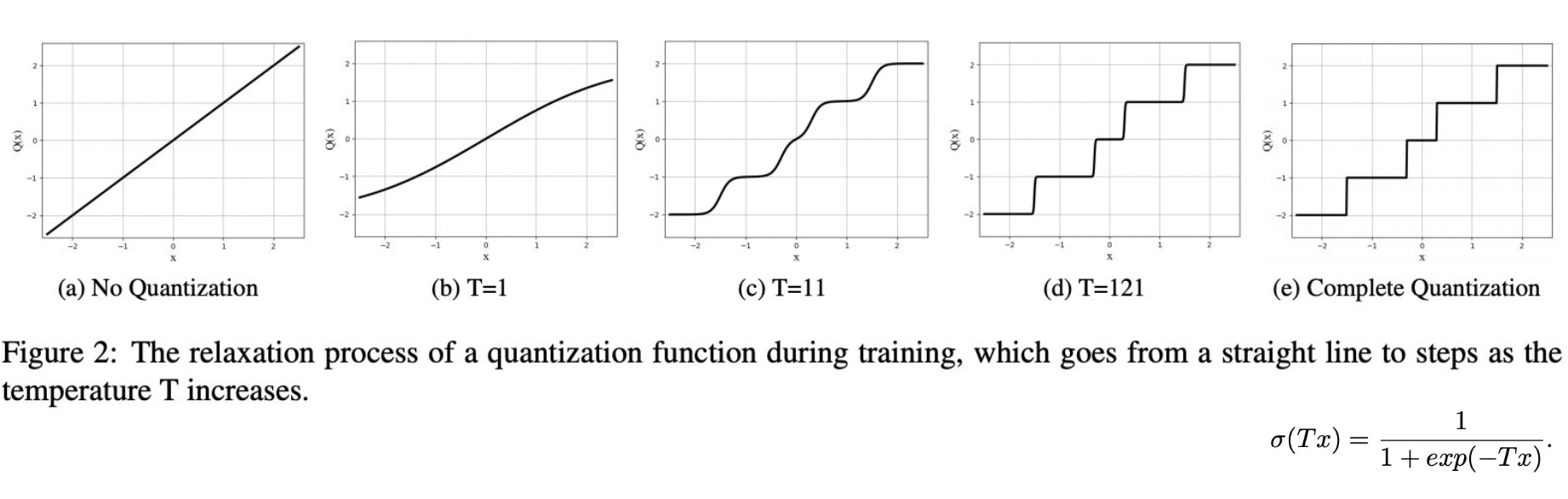
- DOREFA-NET: TRAINING LOW BITWIDTH CONVOLUTIONAL NEURAL NETWORKS WITH LOW BITWIDTH
GRADIENTS - Binarized Neural Networks
여러 Quantization 방법
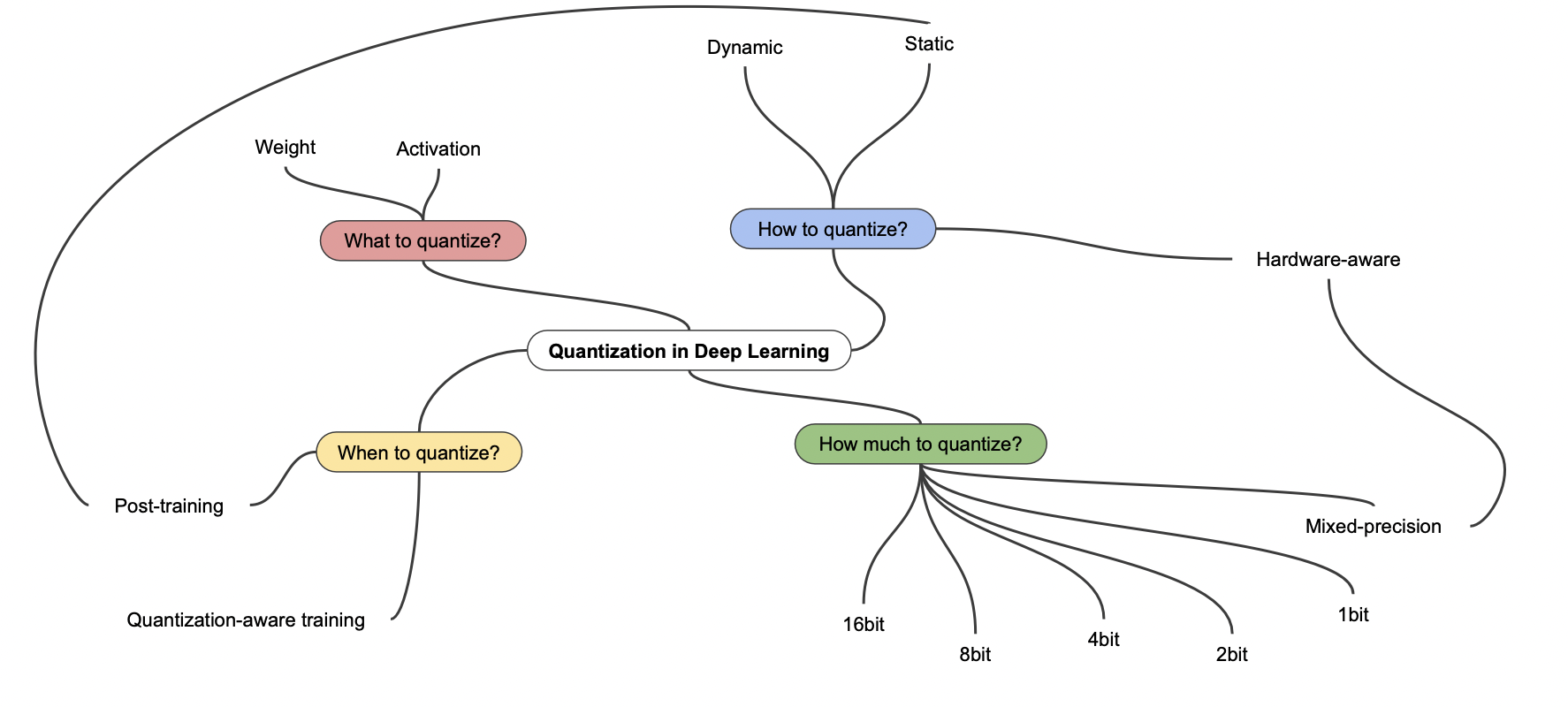
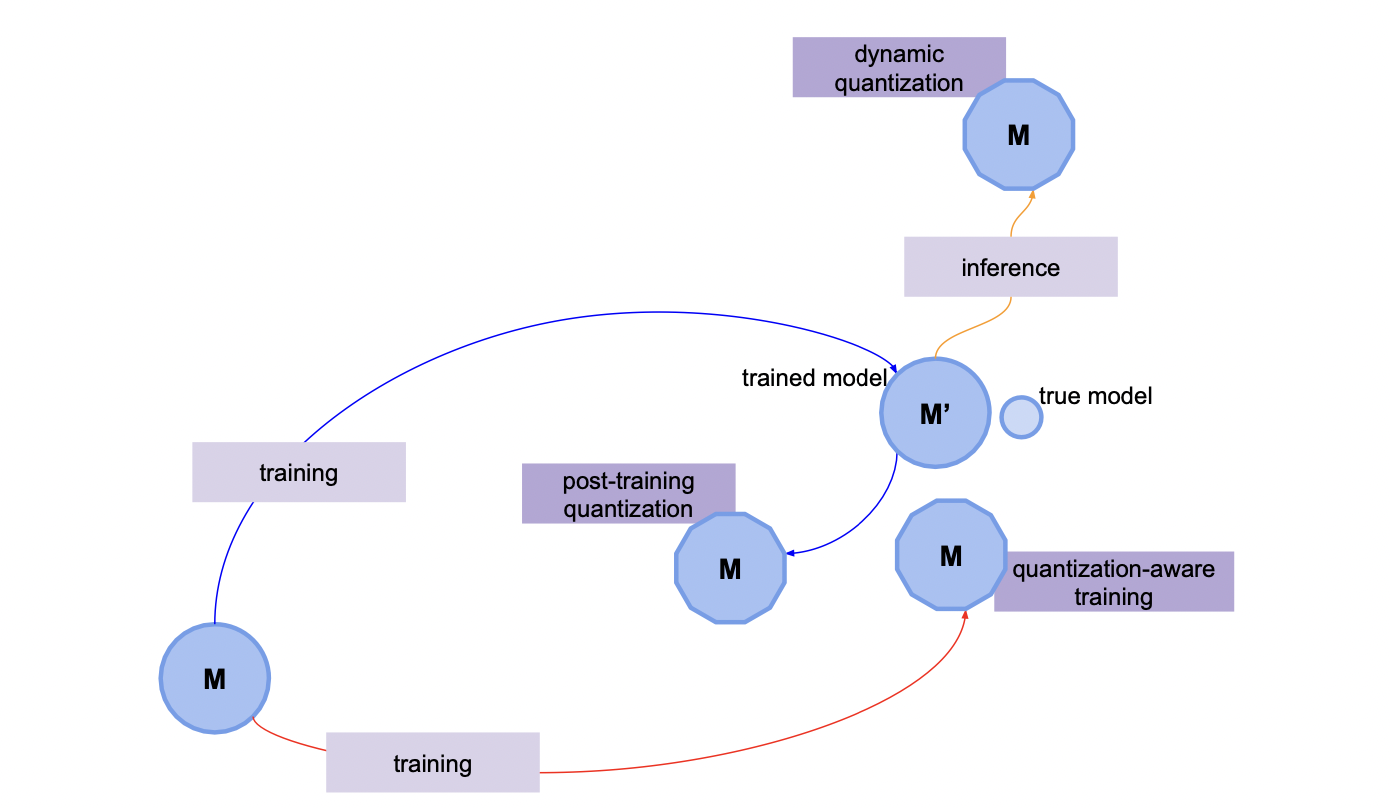
Dynamic quantization
학습이 완료된 모델의 모든 웨이트에 대해 inference 타임에만 양자화를 수행하는 방법이다.
inference 가 끝나면 웨이트를 원래대로 돌려 놓는다.
Static quantization (Post-training)
학습 과정에서 반복적으로 양자화를 수행하는 방법이다.
웨이트 뿐만 아니라 활성함수에도 적용이 된다.
Quantization-aware training
fake node 를 통해 양자화될 것을 인지하며 학습하는 방법이다.

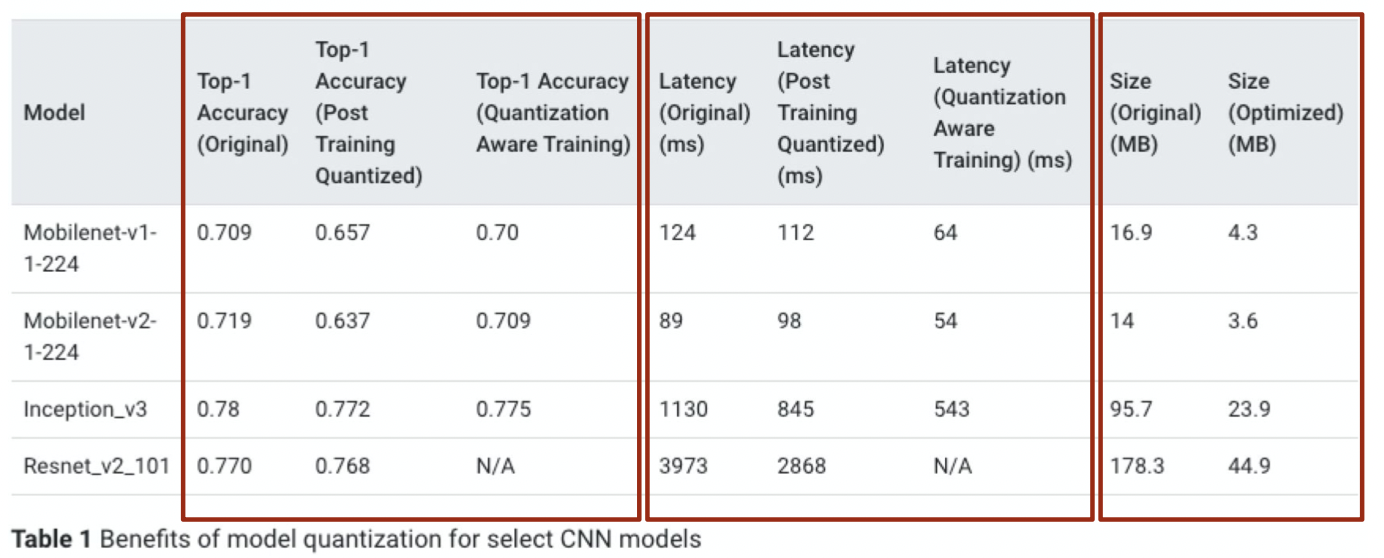
Quantization 결과
양자화된 모델의 정확도는 내려갔지만 속도는 빨라졌음을 확힌할 수 있다.
참조
BoostCamp AI Tech
