[Image Processing] Lecture 10.2 - Lossy Compression : JPEG Algorithm

1. JPEG Algorithm

• The JPEG Algorithm : 더 높은 압축률 달성을 위해 일부 데이터의 손실을 허용하는 기법. 사진 압축을 위해 개발된 표준 알고리즘이다.

  • 특히 인터넷과 같이 용량에 제약이 큰 환경에서 사용하기 적합하다.

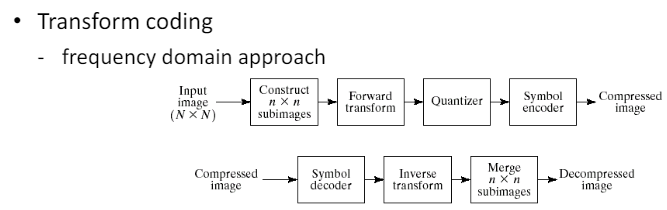
  • Transform Coding을 기반으로 한 알고리즘이다.

    • 즉, 공간 도메인(이미지 도메인)을 주파수 도메인으로 변환하여 압축을 진행한다.

    • 복호화 과정에선, 주파수 도메인을 공간 도메인으로 변환하는 과정을 거친다.

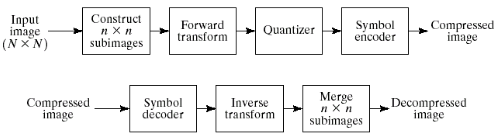
• JPEG Algorithm Process

  • 압축 과정

    • Input Image (M * N) : 원본 이미지를 입력 받는다.

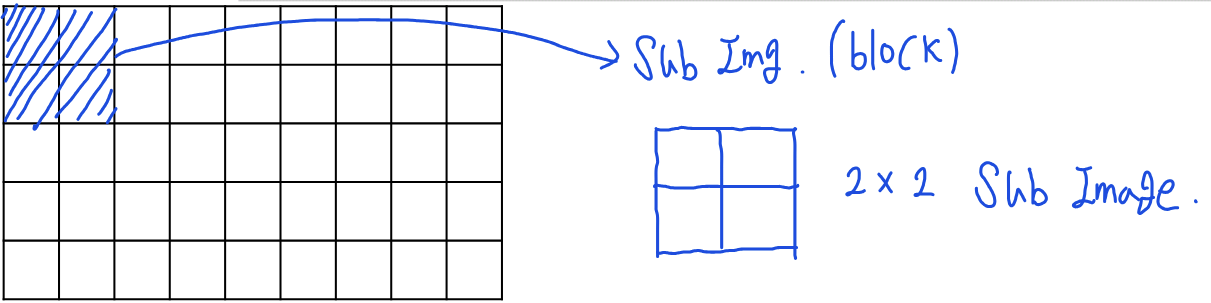
    • Construct subimages (n * n) : 원본 이미지를 n * n 크기의 하위 이미지로 나눈다.

    • Forward transform (전방 변환) : DCT 적용. 하위 이미지를 주파수 도메인으로 변환한다.

    • Quantizer (양자화) : 주파수 영역 데이터를 양자화하여 데이터의 크기를 줄인다.

    • Symbol Encoder : 양자화된 데이터를 심볼로 인코딩하여 압축된 이미지를 생성한다.

  • 복원 과정

    • Sybol Decoder : 압축된 이미지를 심볼 디코더를 사용해 디코딩한다.

    • Inverse transform : 디코딩된 데이터를 역 변환하여 이미지를 주파수 영역에서 다시 공간 영역으로 변환한다.

    • Merge subimages (하위 이미지 합병) : 역 변환된 하위 이미지를 합쳐서 원래 크기의 이미지로 복원한다.

    • Decompressed image (이미지 복원) : 최종적으로 복원된 이미지를 얻는다.

• Transform Coding (변환 코딩) : 상대적으로 덜 중요한 시각 정보인 고주파 성분을 제거하기 위해 이미지 데이터를 주파수 영역으로 변환하는 것이다.

• Discrete cosine transform (DCT) : 데이터를 주파수 영역에서 표현하여 데이터의 중요도에 따라 값을 분리(고주파를 제거)하기 위해 사용되는 방법이다.

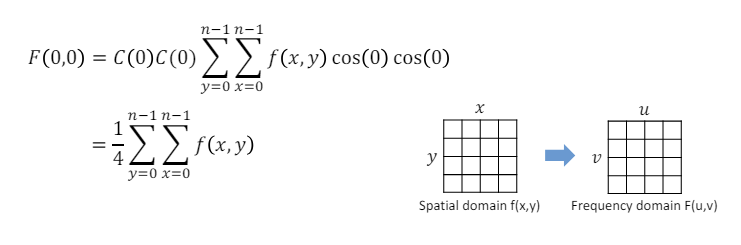
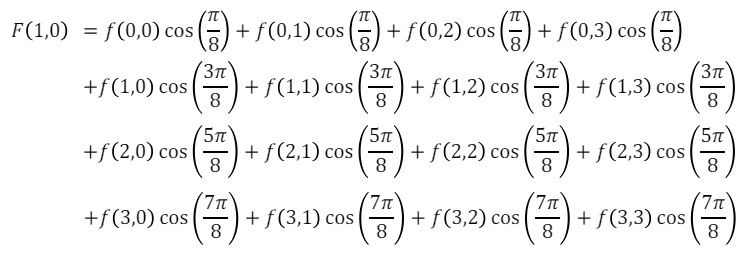
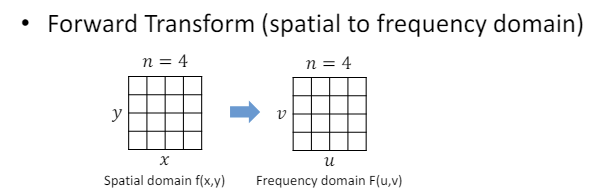
  • Forward 2-D DCT : 공간 영역 이미지 데이터 $\rarr$ 주파수 영역 데이터

    $F(u,v) = C(u)C(v)\sum_{y=0}^{n-1}\sum_{x=0}^{n-1}f(x,y)cos(\frac{(2x + 1)u\pi}{2n})cos(\frac{(2y + 1)v\pi}{2n}) \\ if : C(0) = \sqrt{\frac{1}{n}} \\ else : C(w) = \sqrt{\frac{2}{n}}$

    • $f(x,y)$ : 입력 이미지의 픽셀 값. 공간 영역의 이미지 데이터이다.

    • $F(u,v)$ : 출력 DCT 계수. 이미지가 주파수 영역으로 변환된 데이터이다.

    • $\sum_{y=0}^{n-1}\sum_{x=0}^{n-1}$ : n * n 크기의 블록에서 모든 픽셀의 합산을 의미한다.

    • $cos(\frac{(2x + 1)u\pi}{2n})cos(\frac{(2y + 1)v\pi}{2n})$ : 변환 함수로, 각각 x와 y방향의 주파수 성분을 계산한다. 즉, 이미지 데이터를 주파수 영역으로 변환하기 위한 함수이다.

    • $C(u)C(v)$ : 정규화 상수로, DCT 변환을 통해 얻어진 주파수 성분들이 서로 독립적이고 상호 간섭이 없도록 하기 위해 사용한다.

    • $w = 0$ : DC 성분을 나타내며, 이는 이미지의 평균 밝기와 비슷한 의미를 갖는다.

    • $w != 0$ : DC가 아닌 다른 주파수 성분을 나타낸다.

  • Inverse 2-D DCT : 주파수 영역 데이터 $\rarr$ 공간 영역 이미지 데이터

    $f(x,y) = \sum_{u=0}^{n-1}\sum_{v=0}^{n-1}F(u,v)C(u)C(v)cos(\frac{(2x + 1)u\pi}{2n})cos(\frac{(2y + 1)v\pi}{2n})$

1-1. Encoding

• JPEG 알고리즘의 진행 과정에 대해서 알아보자.

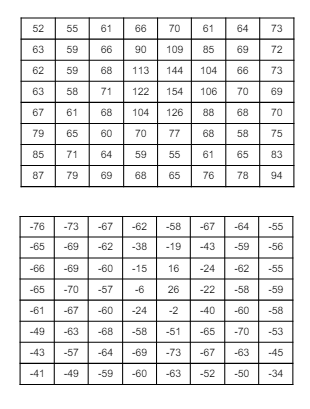
  1). 모든 픽셀에 대해서 128 빼기

  • 이미지의 픽셀 값은 보통 0에서 255 사이의 값을 가진다.

  • 이를 -128에서 127까지의 값을 갖도록 이동시킨다.

  • 즉, 이 과정을 통해 각 픽셀 값들이 0을 기준으로 분포하도록 한다.
    

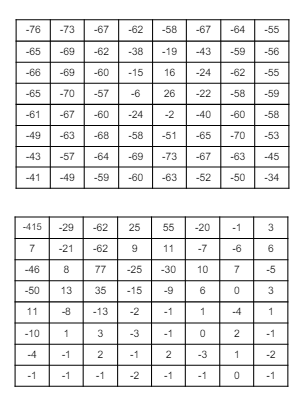
  2). DCT 진행 : $n * n$ 크기의 공간 도메인을 주파수 도메인으로 변환. $(n = 8)$

  • 각 블록이 주파수 영역으로 변환된다.

  • DC 성분 : 첫 번째 값으로, 밝기 성분으로 볼 수 있다.

  • AC 성분 : 픽셀 사이의 변화량으로 볼 수 있다.

  • 저주파 성분은 이미지의 큰 변화를 나타낸다.

  • 고주파 성분(상대적으로 큰 값들)은 이미지의 작은 변화를 나타낸다.

  • DC에서 멀어질수록 AC 값이 작아지는 경향이 있다.

  • 0에 가까운 값들은, 시각 정보에 크게 중요하지 않은 픽셀들이다.

  3). 양자화 + 임계값 처리(Thresholding)

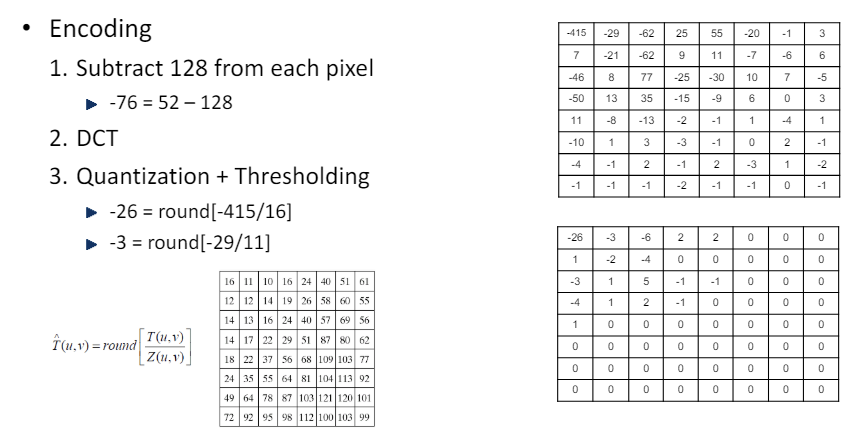
  • 이와 같은 과정을 거치는 이유는, 값을 작게 만듦으로써 압축률을 높이기 위함이다. 즉, -415보다 -26이 당연하게도 더 적은 비트를 갖고 표현할 수 있다.

  • 양자화 행렬은 고주파 성분으로 갈수록 큰 값을 가진다. 이는 저주파 성분이 더 중요한 정보를 포함하기 때문이다. 더 큰 값으로 나눈다는 것은, 그만큼 데이터 손실률이 높다는 뜻과 동일하다.
    

  • 임계값 처리 : 양자화 진행 후, 값이 매우 작은 성분들은 전부 0으로 설정한다. 이 값들은 추후 이미지를 복원할 때 큰 의미를 갖지 못한다고 가정하는 것이다. 즉, 데이터 손실을 감안하더라도 압축률을 높이기 위한 과정이다.

  • 이 과정에서 가장 많은 데이터 손실이 발생한다.

  • 예를들어, $-415 / 16 = -26$이 되었지만, 추후 복원 과정에서 $-26 * 16 = -416$이다. 즉, 오차가 발생(데이터 손실)한다.

  • 또한 매우 작은 값들을 전부 0으로 설정하기 때문에, 이 모든 값들은 데이터 복원이 불가능하다.

  4). 지그재그 스캔 (Zigzag Scanning)

  • EOB는 해당 값 이후부턴 전부 0 값을 갖는다는 것을 나타낸다.

  • 일반적인 직선 스캐닝보다 지그재그 스캐닝이 0을 연속적으로 존재하도록 하기에 유리하다. 즉, 연속적인 값을 처리하는 알고리즘(RLE) 등을 활용하여 압축률을 높이기 위해 이런 스캐닝 방식을 사용한다.

  5). 엔트로피 코딩 (Entropy coding) : Huffman Coding + Run-Length Encoding(RLE)

  • DC

    • DC 성분의 경우 이웃 블록끼리의 차이(Residual)을 적용하여 값을 더 작게 만들어 압축률을 높인다. 위에서 설명했듯이, 더 작은 값일수록 압축에 유리하다.

    • 위 경우, DC 성분의 경우 왼쪽 블록의 값이 (-17)이라고 가정하에 진행하였다.

    • 여기서 -9에 해당하는 category = 4이고, $9 = 1001_{(2)}, -9 = 0110_{(2)}$이다. 따라서 category(base code)와 실제 값을 붙여 표기하면, DC 성분의 최종적인 코드는 $1010110_{(2)}$이 된다.

  • AC

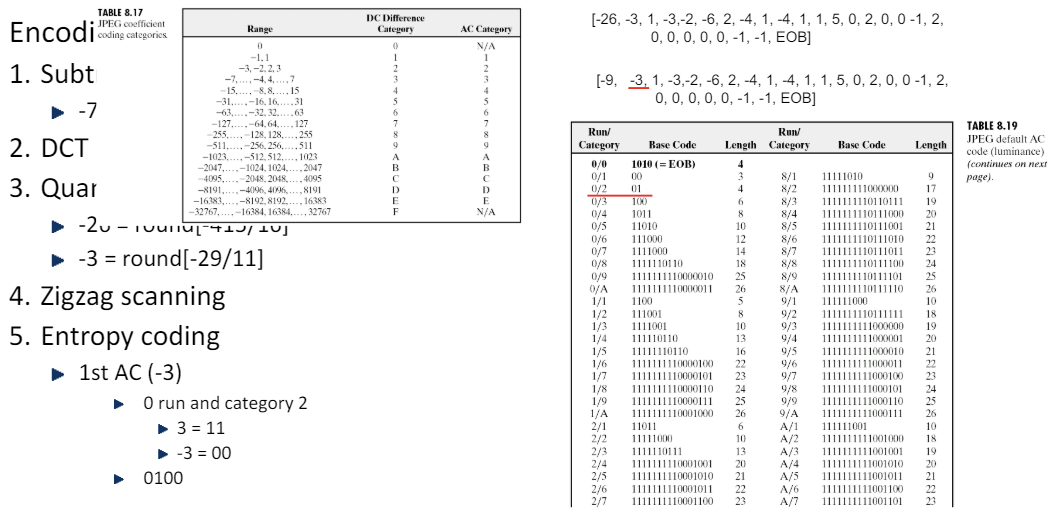
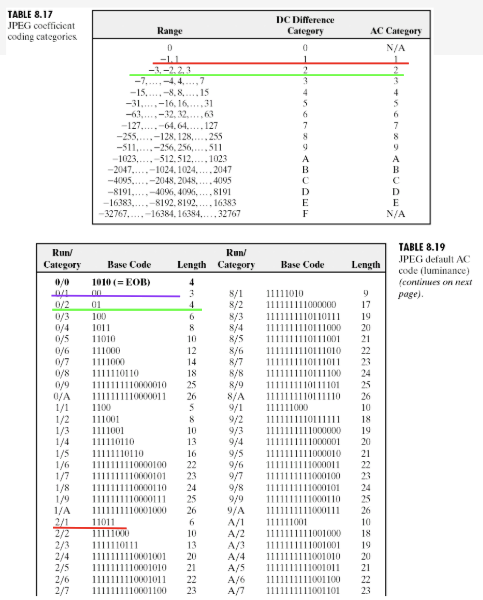
    • AC 성분의 경우 Residual을 적용하지 않아도 이미 충분히 작으므로, 해당 값을 그대로 사용한다.

    • run/category : category 앞 부분(run)은 현재 값(-3) 앞에 0이 몇 개가 있는지에 대한 표시이다.

    • 따라서 위 경우, -3 앞에 0이 없으므로 category = 2이므로, -3은 0/2에 해당한다.

    • $base code = 01, -3 = 00_{(2)}$이므로, 최종적인 코드는 $0100$이 된다.

    • (0, 0, -1)의 경우, 0이외의 다른 값이 나올 때까지 그룹화하는 것이므로, 이렇게 묶여서 비트화가 된다.

    • run = 2가 되며, -1은 카테고리가 1이므로, 2/1에 속한다.

    • $2/1 = 11011$이며, $-1 = 0_{(2)}$이므로 최종적으로 (0, 0, -1)에 대한 코드는 $110110_{(2)}$이 된다.

    • EOB는 "이후부터 존재하는 모든 값은 0"이라는 특수한 표시이다.

위 과정을 모두 거친 결과

원본 : 64 pixels, each pixel has 8bits = 512 bits

압축 후 : 92bits

1-2. Decoding

• JPEG Algorithm의 Decoding 과정에 대해 알아보자.

  • Encoding 과정의 마지막 과정인 허프만 코딩과 RLE는 무손실 압축 기법이다. 따라서 Entrophy Decoding 과정에선 손실이 발생하지 않는다.

  • Denormalizing (임계값 처리 + 양자화의 역연산) 과정에서 손실이 발생한다. 인코딩 과정에서 양자화를 진행할 때, 나눗셈의 결과를 모두 정수로 처리했기 때문에 오차가 발생한다. 또한, 임계값 처리 과정에서 매우 작은 값들은 전부 0으로 처리했기 때문에 이 부분은 복원이 불가능하다.

  • Inverse DCT, 128을 더하는 과정에서 손실은 발생하지 않는다.

  • 결과적으로, Decoding한 결과는 Encoding을 진행하기 전과 근사한 값을 갖지만, 완벽하게 같은 값을 갖진 못한다.

• Noise 육안상 큰 차이가 없어보이지만, 실제 노이즈가 생긴 상태이다.

  • 양자화 행렬 값에 따른 노이즈

    • Q를 2배 증가

    • 5배 증가

    • 10배 증가

  • 양자화 값이 커지면 커질수록 압축률은 커질 수 있으나, 데이터 손실이 커지는 것을 알 수 있다.
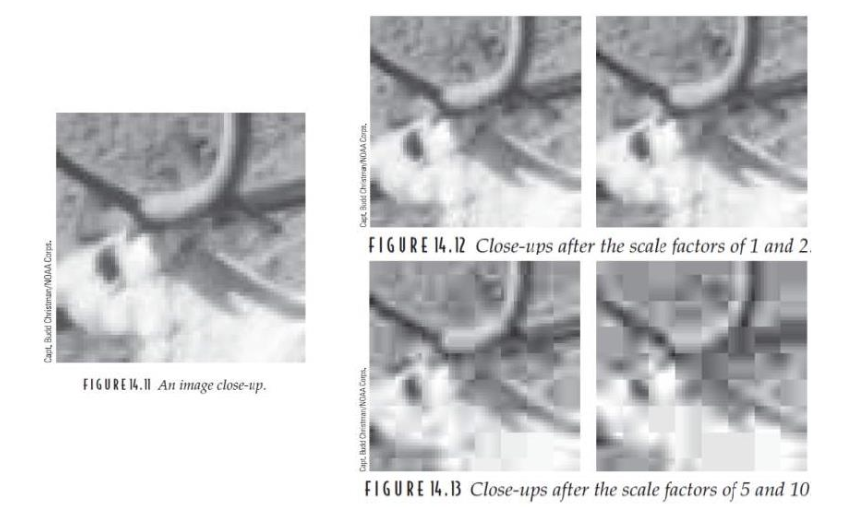