[Image Processing] Lecture 10.1 - Lossless Compression : Huffman Coding, Run-Length Encoding

1. Compression

• Lossless Compression (무손실 압축) : 원본 데이터의 모든 정보가 보존되는 압축 방식이다. 주로 텍스트 파일이나 소프트웨어 파일 같이 정보의 손실이 허용되지 않는 데이터에 사용된다. Zip 파일이 대표적인 예시.

• Lossy Compression (손실 압축) : 압축 과정에서 일부 데이터가 제거되며, 원본 데이터와 압축을 푼 후의 데이터 사이에 차이가 있다. 주로 이미지, 비디오, 오디오 파일과 같은 경우에 사용되며, JPEG, MP3가 대표적 예시.

2. Lossless Compression

2-1. Huffman Coding

• Huffman Coding : 허프만 코딩은 주로 무손실 압축 기법으로, 효율적인 압축을 위해 사용된다.

  • Key idea : 발생 빈도가 높은 정보에 짧은 비트를 할당하고, 빈도가 낮은 정보에는 긴 비트를 할당한다. 이 방식을 통해 효율적인 압축을 기대해볼 수 있다.

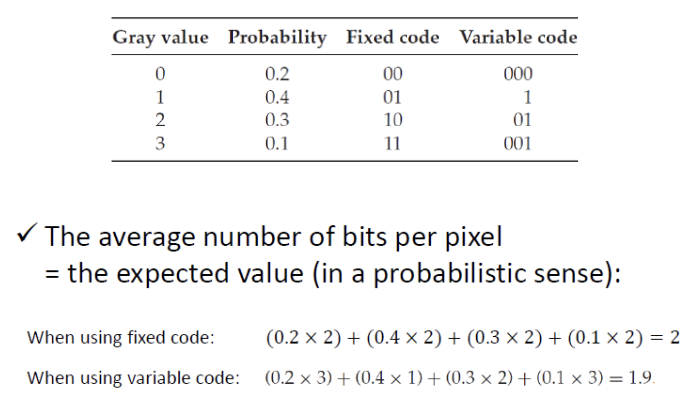
  • 각 픽셀의 평균 비트수 = 기대값이다.

  • fixed code 방식보다 varialbe code 방식을 사용하였을 때 사용되는 평균 비트 수가 더 적다.

  • Entropy $H$ : 어떤 정보가 발생할 확률이 주어졌을 때, 이를 인코딩하기 위해 필요로 하는 비트의 이론상 최소값이다.

    • $p_i$ : $i$번 째 심볼의 확률

    • $L$ : 심볼의 총 개수

    • 위의 경우 엔트로피 계산은 다음과 같다.
      $H = -(0.2log_2(0.2) + 0.4log_2(0.4) + 0.3log_2(0.3) + 0.1log_2(0.1)) = 1.8464$

• Huffman Coding Process

  1). 이미지의 각 그레이 값(0 ~ 255)에 대한 빈도를 계산(이는 히스토그램으로 나타낼 수 있다)하고, 이를 바탕으로 각 픽셀 값에 대한 확률을 계산한다.

  2). 확률이 가장 낮은 두 그레이 값(노드)을 합쳐 새로운 노드를 만든다. 이 과정을 모든 그레이 값이 트리에 포함될 때까지 반복한다.

  3). 트리의 루트에서 시작하여 각 노드에 대해 왼쪽 가지에 0, 오른쪽 가지에 1을 할당한다.

  4). 루트 노드에서 각 그레이 값의 노드까지의 경로를 따라 0과 1을 조합하여 허프만 코드를 생성한다.

  5). 이렇게 생성된 코드는 각 그레이 값에 대응되며, 이 코드들을 사용하여 파일을 압축한다.

• 예제

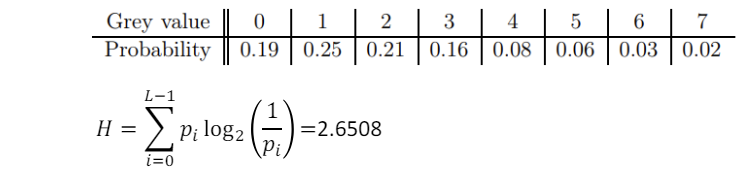
  • 위와 같은 경우, 8가지 픽셀 값을 나타내기 위해선 3bit이 필요하다.

  • 하지만 Entropy 공식에 의한 이론적으로 필요한 최소 비트 $H = 2.6508$이다.

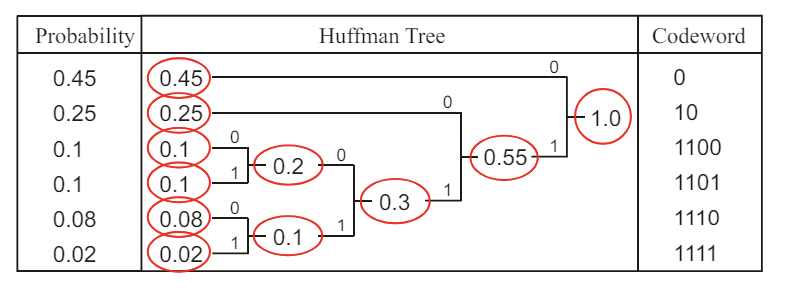
  • 각 픽셀에 대한 확률을 구했으니, Binary Tree를 구성한다.

  • 1.0부터 해당 확률까지 트리를 따라가며 허프만 코드를 생성한다.
    

  • 이 생성된 비트들에 대한 평균 비트 수는 2.7이다.

  • 위에서 계산한 Entropy 값에 근접함을 알 수 있다.

허프만 코드의 장단점

• 장점
  1). 전체적인 데이터 크기를 줄여 효율적으로 압축할 수 있다.

  2). 데이터 손실이 없다. 즉, 복호화 과정을 거친 데이터는 원본 데이터와 동일하다.

• 단점

1). 데이터 발생 빈도의 차이가 적은 경우, 압축 효율이 낮다.

2-2 Run-length Encoding

• Run-length Encoding (RLE, 연속 길이 부호화) : 반복되는 데이터를 압축하여 용량을 줄이는 기법이다. 이 방법은 이진 이미지나 텍스트 파일 같이 동일한 값이 연속적으로 반복되는 경우에 주로 사용된다.

  • Key idea : 연속적으로 반복되는 숫자(0 혹은 1)가 존재하는 경우, 해당 숫자가 반복된 횟수를 같이 저장한다.

  • 예제 1 : 0의 개수와 1의 개수를 번갈아가며 압축하는 방법.

    • row 1 : 0이 1개, 1이 2개, 0이 3개 연속되므로 (123)이 된다.

    • row 2 : 인코딩 해보면, (231)이 된다.

    • 위 과정을 반복한 결과 : $(123)(231)(0321)(141)(33)(0132)$

  • 예제 2 : 1이라는 숫자를 기준으로 반복되는 숫자를 압축하는 방법.

    • row 1 : 1은 2번 째 자리에서부터 길이 2만큼 연속되므로 (22)

    • row 2 : 1은 3번 째 자리에서부터 길이 3만큼 연속되므로 (33)

    • row 3 : 1은 1번 째 자리에서부터 길이 3만큼 연속되고, 6번 째 자리에서부터 시작해서 길이 1만큼 연속되므로 (1361)

    • 위와 같은 과정을 반복한 결과 : $(22)(33)(1361)(24)(43)(1152)$

RLE 장단점

• 장점 : 간단하고 구현이 쉬우며, 반복되는 데이터가 많은 경우 압축률이 높다.

• 단점 : 데이터에 반복이 거의 없는 경우, 압축 효과가 거의 없거나 오히려 압축 후 데이터가 커질 수 있음.