
1. Parametric Transformation
-
Parametric (global) warping : 파라메트릭 왜곡에서 변환 는 좌표를 변경하는 알고리즘으로, 점 의 좌표를 새로운 좌표 로 변환한다.
- Global transform T : 전역 변환 의 의미는, 어떤 점 p에 대해서도 동일하게 동작한다는 것이다.
-
Transform : 이미지의 위상 변화는 매우 다양하게 나타날 수 있다.

1-1. 2D Transformation
-
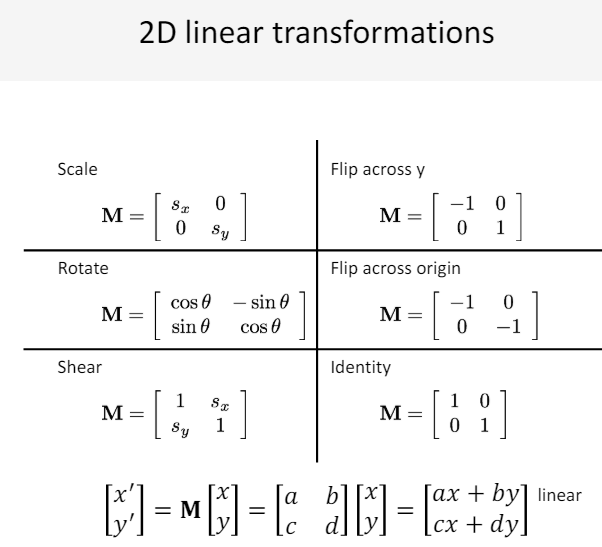
Uniform scaling : 높이와 너비를 모두 동일한 비율로 변화시키는 것.
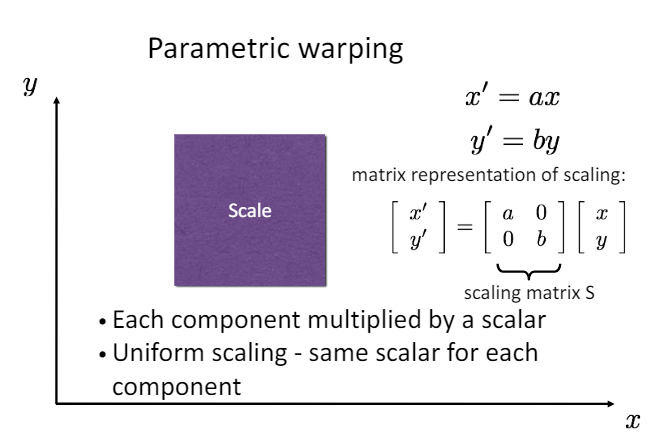
- 행렬 형태로 다음과 같이 표현할 수 있다.
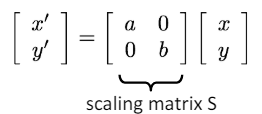
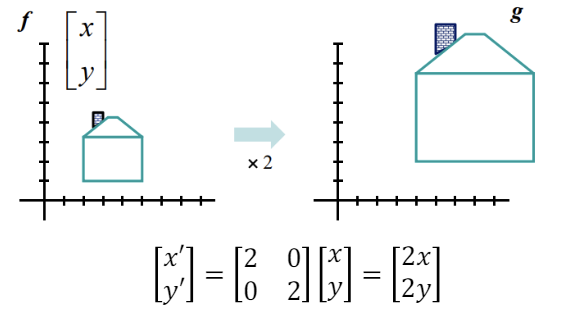
- 행렬 형태로 다음과 같이 표현할 수 있다.
-
Non-uniform scailng : 높이와 너비를 다른 비율로 변화시키는 것.
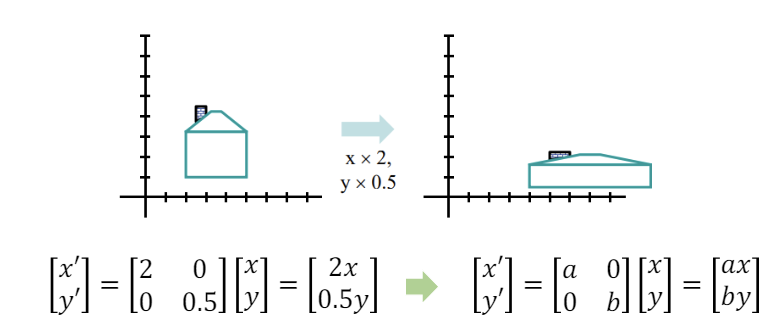
결론적으로, Scaling은 각 좌표값에 Scalar 값이 곱해지는 형태로 표현할 수 있다.
-
Shear : 이미지의 기울기를 변화시키는 것.
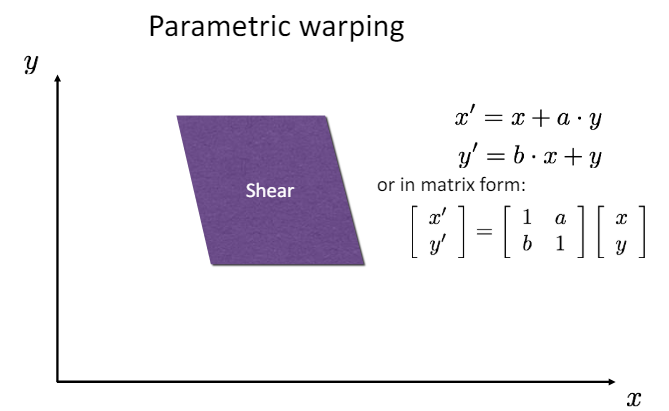
-
rotation : 이미지가 특정 각도만큼 회전하는 것.
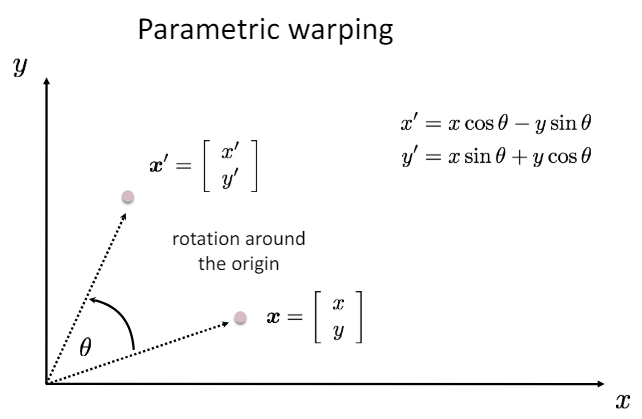
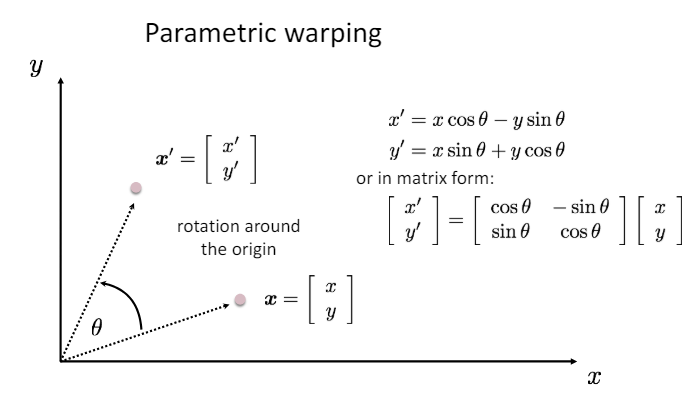
-
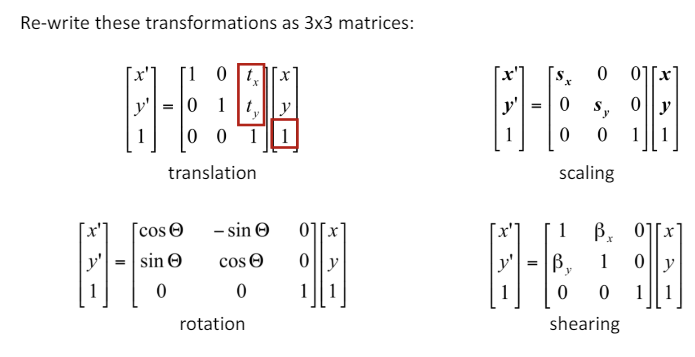
결론적으로, 행렬로 표현할 수 있는 2D Transformation 식은 다음과 같이 행렬 을 통해 표현할 수 있다.
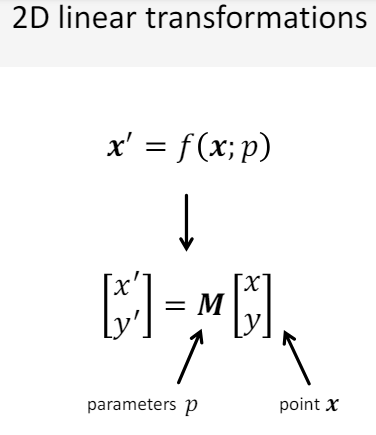
- 이는 linear transformation이라고도 불리운다.
-
Non-linear transformation
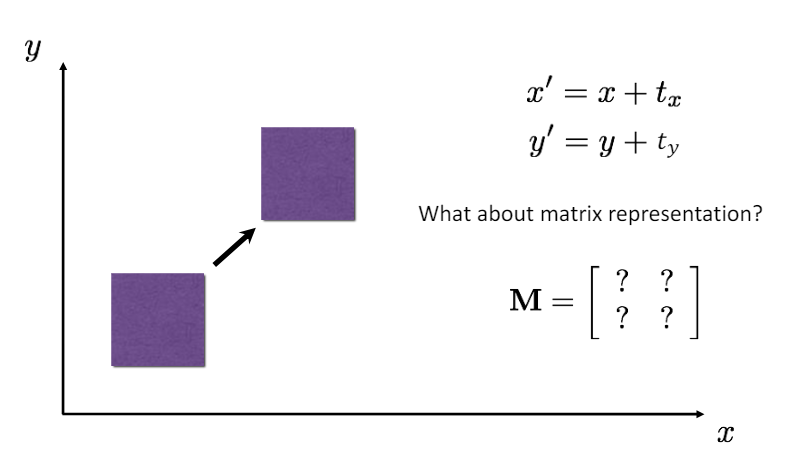
-
위 그림과 같이 바뀐 좌표값을 이라 표현할 수 있다.
-
위와 같은 경우, 행렬 M의 곱으로 나타낼 수 없기 때문에 2D Transformation(linear transformation)이 아니다.
-
대신, 행렬 곱으로 표현하기 위해 Homogeneous coordinates를 사용할 수 있다. 이는 2D Point에 의미 없는 값 1을 붙여서 3D Vector로 만들어 사용하는 방식이다.
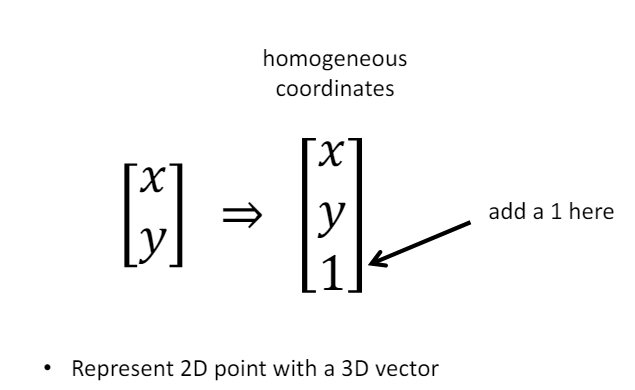
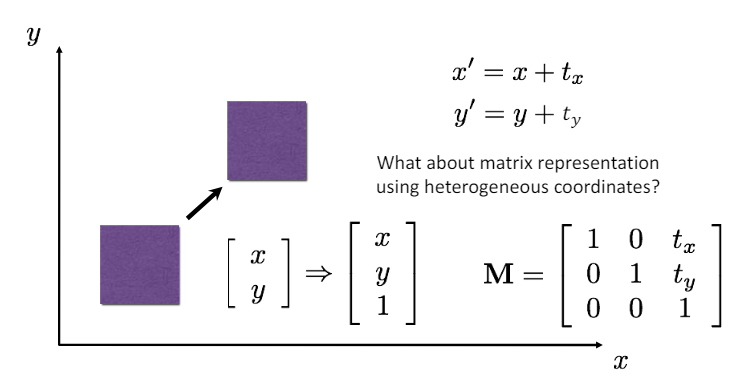
-
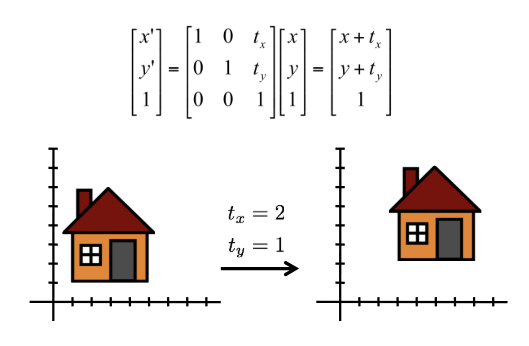
Homogeneous coordinates (동차 좌표) : 평행 이동같은 변환은 2 * 2 행렬로 표현할 수 없다. 따라서 평행 이동을 행렬로 표현하기 위해서 동차 좌표 개념을 도입했다. 즉, 모든 변환을 3 * 3 행렬로 표현할 수 있다는 것이다.
-
-
Matrix Composition (행렬 조합) : 여러 변환을 따로 진행하는 것보다, 하나의 행렬에 합쳐서 한번에 처리하는 것이 훨씬 효율적이다. 이를 위해 동차 좌표 개념을 도입한 것이다.

- 위와 같이 Translation, Rotation, Scaling을 모두 하나의 행렬로 결합한 후 좌표에 곱하는 방식으로 좌표를 변환할 수 있다.
- 위와 같이 Translation, Rotation, Scaling을 모두 하나의 행렬로 결합한 후 좌표에 곱하는 방식으로 좌표를 변환할 수 있다.
결론적으로, 위와 같이 행렬들을 한번에 곱한 후 좌표에 곱하는 방식을 위해서 Translation를 굳이 3 * 3 행렬로 표현하도록 한 것이다.
1-2. Classification of 2D Transformations
-
Euclidean Transformation (rigid, Rotation + Translation) : 유클리드 변환은 물체의 형상을 유지하면서 위치와 방향만을 바꾸는 변환이다. 즉, 회전과 평행 이동의 합으로 볼 수 있다.
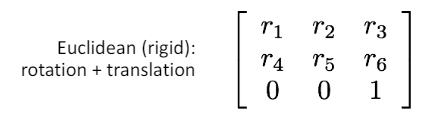
-
는 회전을 나타내는 요소이다.
-
는 평행 이동을 나타내는 요소이다.
-
은 동차 좌표를 사용하기 위해 추가한 값이다.
-
결론적으로, 유클리드 변환은 다음과 같은 행렬로 표현할 수 있다.
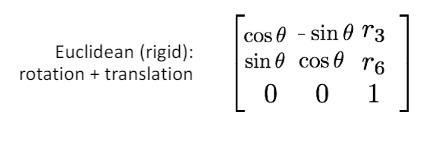
-
-
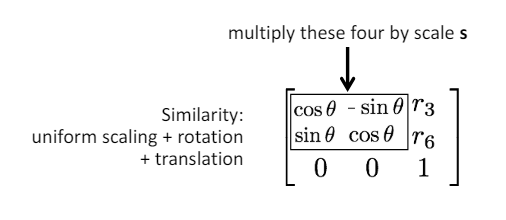
Similarity Transformation : 유클리드 변환 + Uniform Scaling
-
회전을 나타내는 값인 삼각함수의 네 값에 동일하게 Scalar s를 곱한 것으로 Uniform Scaling을 추가할 수 있다.
-
즉, 유클리드 변환 + Uniform Scaling
-
-
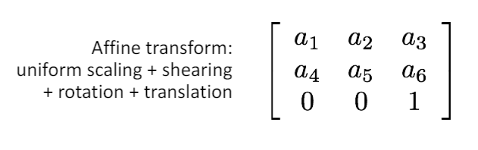
Affine Transformation : Similarity Transformation + Shearing
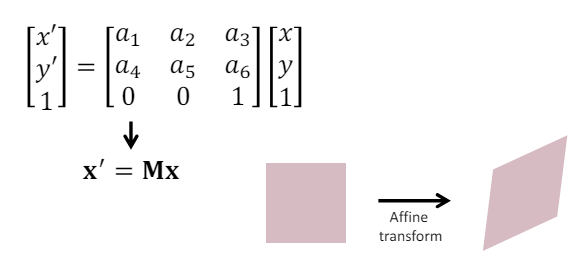
-
아핀 변환은 [Scaling, Rotation, Shear] (Linear transformations) + Translation (평행 이동)이라고 할 수 있다.
-
: 선형 변환 요소
-
: 평행 이동 요소
-
2. Image Warping
-
Image Warping : 이미지 왜곡은 이미지를 특정한 방법으로 변환하는 것을 의미한다. 이때 Warping을 하기 위해선 새로 변형된 이미지를 전부 다 포함할 수 있는 크기의 공간을 새로 만들어야 한다.

- 위와 같이 회전한 결과 일부 좌표가 프레임 좌표를 넘어갈 수 있기 때문에, 이를 포함하도록 하는 크기의 새로운 공간을 선언해야한다.
2-1. Forward Warping
-
Forward Warping : 순방향 왜곡은 원본 이미지에 왜곡을 일으키는 방법이다. 즉, 앞서 배운 여러가지 변환 방법들을 실제 좌표에 적용하여, 원본 이미지의 좌표와 변형 이미지의 좌표를 매핑시키는 것을 의미한다.
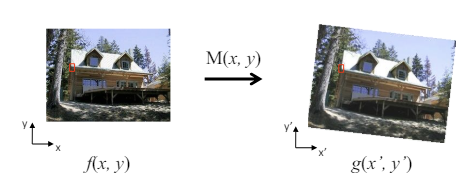
-
좌표 매칭
-
픽셀은 기본적으로 정수값의 좌표를 갖는다고 추정한다.
-
이때, 행렬 M은 여러가지 변환 방법이 포함(특히, cos, sin 연산)되어 있다.
-
따라서 의 계산 결과인 의 좌표가 정수가 아닐 가능성이 매우 높다.
-
따라서 단순히 행렬과 원본 이미지 의 연산으로 의 좌표에 1:1로 매칭하기에는 무리가 있다.
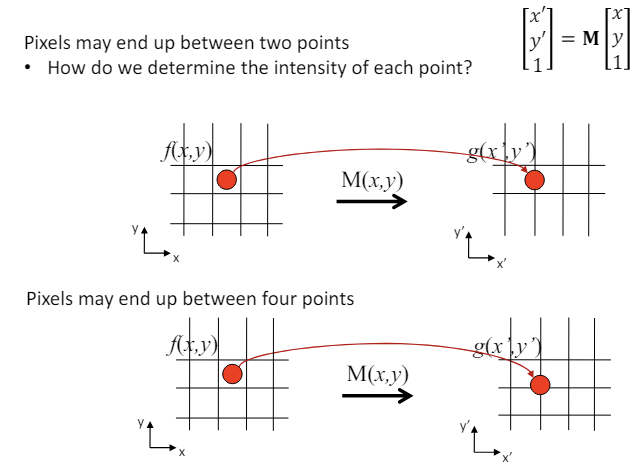
-
-
-
Coordinates Mapping
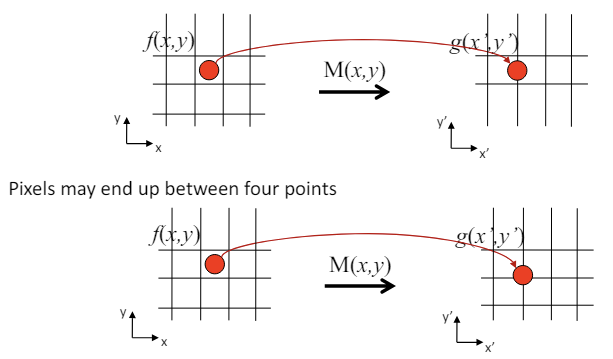
-
그렇다면, 위와 같이 1:1 매칭이 불가능한 상황에선 좌표를 어떻게 매칭해야될까?
-
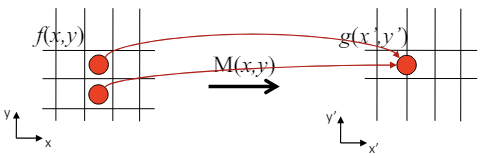
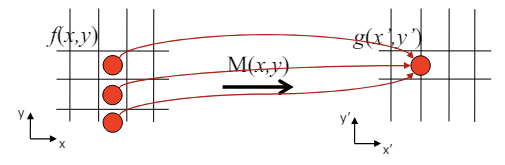
예를 들어 의 좌표가 와 같이 나온다면, 와 같이 걸치는 모든 좌표에 같은 값을 매칭하는 방법을 사용한다.
-
두 가지 좌표에 대한 결과가 와 같이 나온다면, 두 의 좌표에 대한 평균 값 를 에 매칭할 수 있다.
-
-
매핑이 1:1 대응이 아니기 때문에, 어떤 좌표에는 아무런 매핑이 발생하지 않을 수 있다. 이런 경우를 빈 공간(Hole)이 발생했다고 한다.
2-2. Backward Warping
-
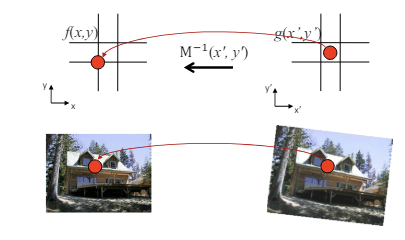
Backward Warping : 역방향 왜곡은, 왜곡된 이미지를 원본의 이미지로 복구하는 방법이다.

-
역방향 Warping의 목적은 다음과 같이 왜곡 이미지 와 Inverse Matrix 의 연산을 통해 원본 이미지인 를 복원하는 것이다.
-
Forward Warping과 마찬가지로, 와 사이에서 1 : 1 좌표 매핑은 어렵다.
-
이를 해결하기 위해 원래 좌표를 추정하는 Interpolation을 사용하게 된다.
-
즉, g의 (x,y) 좌표가 소수라면, 이 값을 추정하기 위해 주변 4개의 pixel 값들 활용한 Bilinear Interpolation을 사용한다.
-
이는 Hole이 발생하는 문제를 해결할 수 있지만, 가중 평균 계산 방법이기 때문에 전체적인 밝기 값이 변화할 수 있다.
-
-
