[Image Processing] Lecture 05 - Image Resizing

1. Image downsampling

• Naïve image downsampling : 이미지의 해상도를 단순하게 낮추는 방법이다.

1-1. Aliasing and Anti-Aliasing

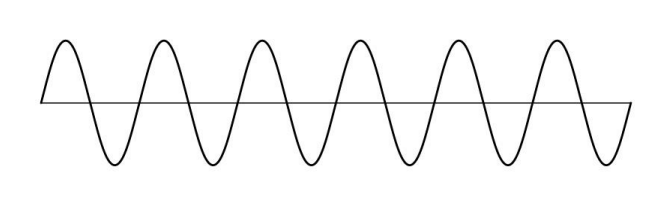
• Aliasing : 아날로그 신호를 디지털 신호로 처리하는 과정에서, 신호가 잘못 해석되는 현상이다.

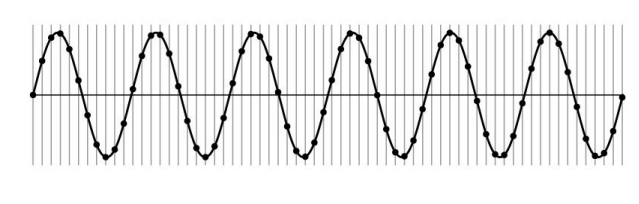
  • 본래 신호의 형태를 추측할 수 있는 경우

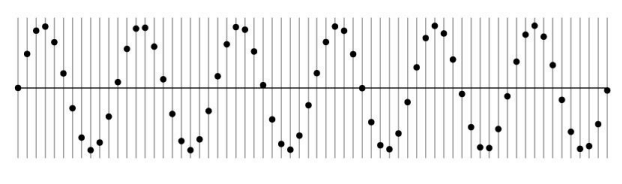
  • 본래 신호의 형태를 추측하기 어려운 경우 : Undersampling $\rarr$ 데이터의 많은 부분에서 손실이 발생하여, 본래의 형태를 추정하기 어렵다.

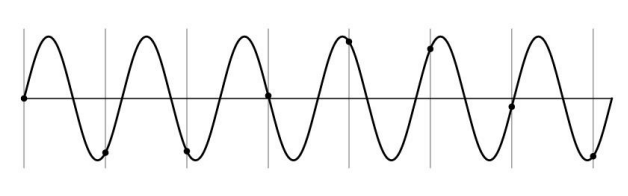
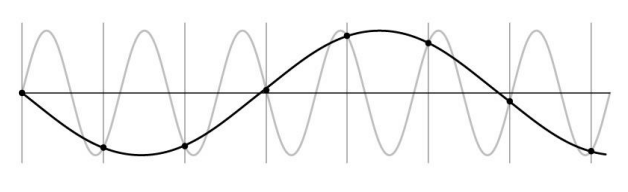
  • 위와 같은 경우, Unsurprising effect, Surprising effect가 발생했다고 볼 수 있다.

    • Unsurprising effect : 샘플링 속도(주파수)가 충분히 높지 않기 때문에, 신호의 세부 정보가 제대로 포함되지 않는 현상이다.

    • Surprising effect : 고주파 성분이 저주파 신호로 잘못 해석되는 현상으로, 원본 신호와는 전혀 다른 신호로 인식되게 만든다.

• Moire : 사진에서 발생하는 Aliasing 현상으로, 주기적인 패턴이 겹쳐질 때 새로운 주기적인 패턴이 발생하는 것이다.

Aliasing 현상은 모두 Sampling rate가 낮기 때문에 발생한다.

• Anti-aliasing : Aliasing 현상을 처리하기 위한 기법이다.

  • Oversampling : 매우 높은 샘플링 속도로 샘플링하여 Signal lost를 최소화하는 방법이다.

  • Smooth the Signal : 신호를 부드럽게 함으로써 잡음을 없앨 수 있다. 이 과정에서 일부 정보는 손실될 수 있지만, Alasing을 방지할 수 있다.

    • Gaussian 필터 적용 : Gaussian 필터를 적용하여 이미지의 고주파 노이즈를 줄인다.

    • 짝수 행 제거

    • 홀수 행 제거

    • 위 과정 반복

    • 결과

1-2. Image Downsampling

• Resize $448 * 448$ to $64 * 64$ : 이미지 size를 $\frac{1}{7}$로 줄이는 과정에 대해 알아보자.

  1). Create new Image : 목표 크기인 $64 * 64$ 크기의 비어있는 새로운 이미지를 생성한다.

  2). Match up coordinates : 새로운 이미지의 각 픽셀 좌표와 원래 이미지의 해당 좌표 사이의 관계를 정의해야한다. 즉, 새로운 이미지의 각 픽셀이 원래 이미지의 어느 위치에 해당하는지 계산한다.

  3). Iterate over new points : 새 이미지의 각 픽셀에 대한 원본 이미지의 위치를 찾고, 그 주변의 픽셀 값을 이용하여 새 픽셀의 값을 결정한다. 이 과정에서 보간법(Interpolation)을 사용한다.

  • 이미지 리사이즈 과정

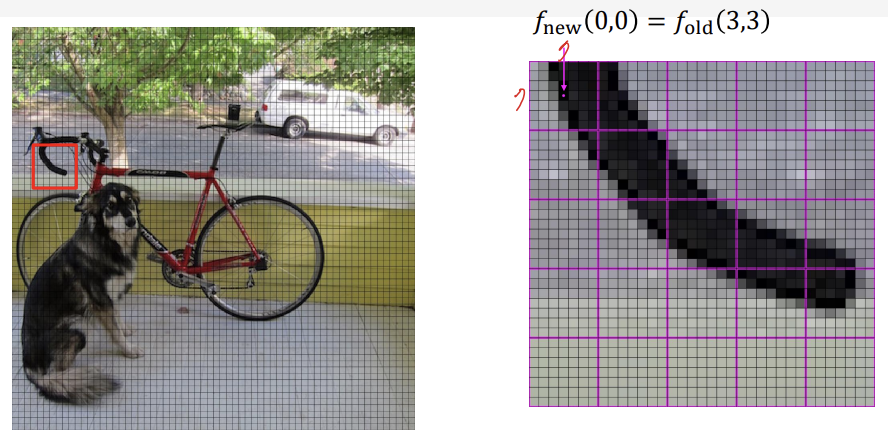
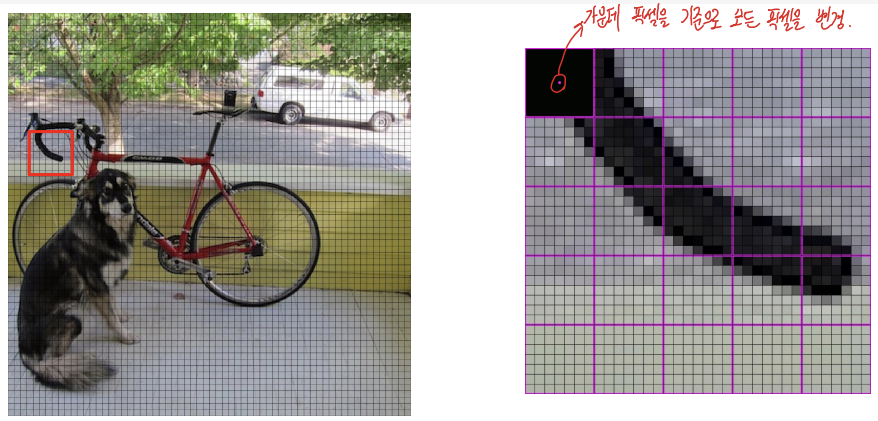
  • 위 방법은 픽셀 중앙값으로 $7 * 7$ 범위의 모든 픽셀 값을 덮어버리는 방식으로, 원본 이미지의 훼손이 심해 왜곡 현상이 발생한다.

  • Smoothing 기법을 활용하여 이 문제를 어느정도 완화 할 수 있다.

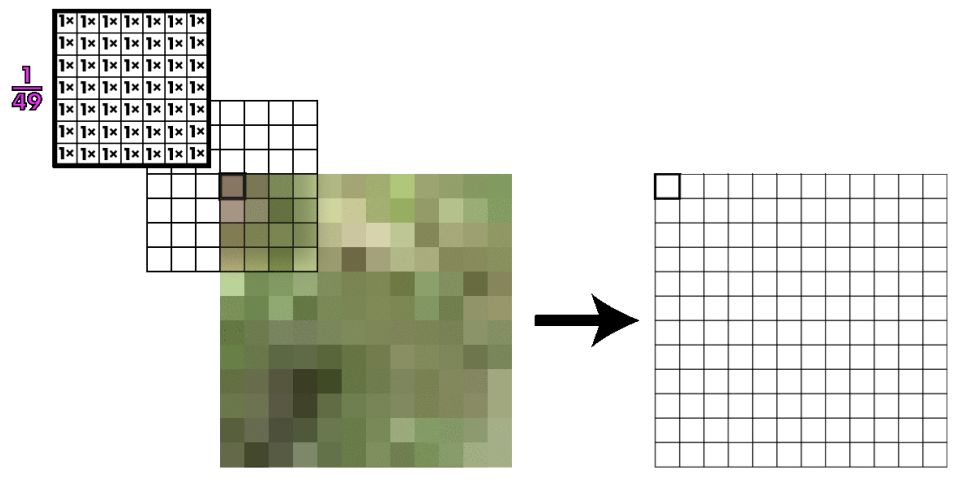
• Gaussian pyramid

  • 이미지 Resizing이 진행 될수록 이미지가 평활화(Smoothed out)된다.

  • 상위 단계(Resize 수준이 높은)로 가도, 주변 픽셀과 차이가 큰 부분은 원본 이미지의 형태를 유지한다.

  • 상위 단계로 올라갈수록, 해상도는 떨어지며 세부 사항이 많이 손실된다. 또한 상위 단계의 이미지는 원본 이미지로 정확히 되돌리기가 어렵다.

2. Interpolation

• Interpolation (보간법) : 원본 데이터에서 좌표가 변화할 때, 각 값들이 어떻게 매칭이 되어야 하는지를 결정하는 방법이다.

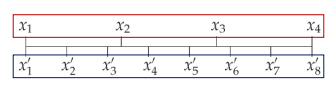
  • ex) 4개의 값이 주어지고, 이를 8개의 값으로 확장

2-1. Nearest Neighbor Interpolation

• Nearest Neighbor Interpolation (NN 보간법) : 이 방법은 새로운 좌표에 가장 가까운 원본 좌표의 값을 그대로 할당하는 방식이다.

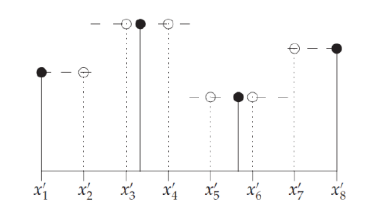
  • 보간을 할 새로운 위치 $x$를 선택하고, 해당 $x$와 가장 가까운 좌표의 값을 그대로 가져온다.

  • 보간을 할 새로운 위치 (x$^\prime$, y$^\prime$)에 대한 계산식은 다음과 같다.

    $f(x^{\prime}) = f([x + 0.5])$

2-2. Linear interpolation

• Liner interpolation (선형 보간법) : 두 좌표 사이의 사이의 값을 추정하기 위해 직선 방정식을 사용하는 방법.

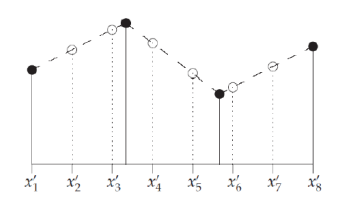
  • 다음과 같은 직선 방정식을 사용한다.
    $f(x) = ax + b$
    • 두 데이터 포인트 $(x_1, f(x_1))$, $(x_2, f(x_2))$가 주어졌을 때, 다음과 같이 계산할 수 있다.
      $\frac{F - f(x_1)}{\lambda} = \frac{f(x_2) - f(x_1)}{1}$
      $F = \lambda f(x_2) + (1 - \lambda)f(x_1)$
    • 위와 같은 식이 성립하는 이유는, 두 데이터 포인트 $(x_1, f(x_1))$, $(x_2, f(x_2))$에 대해서, 닮은꼴이 성립하기 때문이다. (각 점 사이의 거리가 1로 정규화 되어있다는 가정 하에)
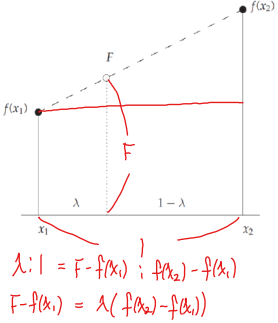
    • 선형 보간은, 결국 가까운 값이 더 많은 가중치를 갖게되는 방식이다.

2-3. Bilinear Interpolation

• Bilinear interpolation (이중 선형 보간법) : 2차원에서 선형 보간을 하는 방법으로, 1차원에서의 선형 보간과 마찬가지 방법이지만, 가로 방향과 세로 방향 총 두 번의 연산을 진행한다.

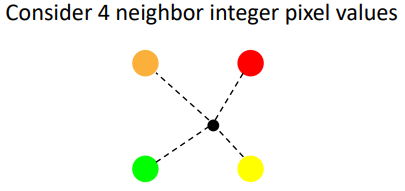
  • 진행 과정

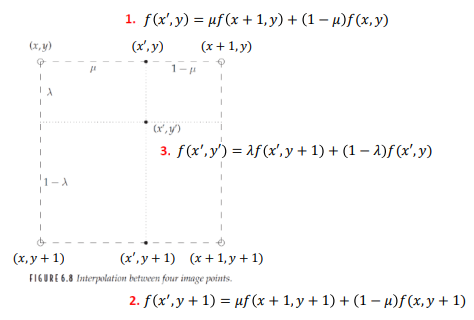
    1). $f(x^\prime, y) = \mu f(x+1, y) + (1 - \mu) f(x, y)$ : 가로 방향으로 두 점 $(x,y), (x+1, y)$ 사이의 선형 보간을 수행한다.

    2). $f(x^\prime, y+1) = \mu f(x+1, y+1) + (1 - \mu) f(x, y)$ : 가로 방향으로 두 점 $(x, y+1), (x+1, y+1)$ 사이의 선형 보간을 수행한다.

    3). $f(x^\prime, y^\prime) = \lambda f(x^\prime, y+1) + (1 - \lambda) f(x^\prime, y)$ : 세로 방향으로 두 점 $(x^\prime, y), (x^\prime, y+1)$ 사이의 선형 보간을 수행한다.

  • 위 과정은 1차원 선형 보간에서와 마찬가지로, 비율에 따른 유도로 알 수 있다.

  • 따라서 $(x^\prime, y^\prime)$은 다음과 같이 나타낼 수 있다.

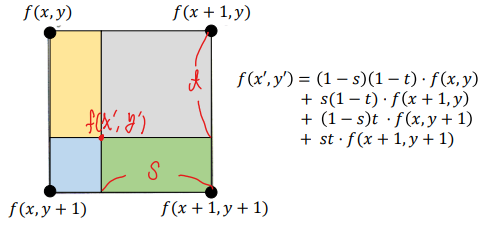
  • 결과적으로, $(x^\prime, y^\prime)$은 주변 4개의 픽셀의 가중합을 통해 구한 것이다. 이때, 모든 가중치의 합은 1(전체 큰 사각형의 넓이)이 된다.

• Bilinear Interpolation vs Nearest neighbor Interpolation : 이중 선형 보간법은 4가지 픽셀 값에 모두 영향을 받지만, NN 보간법은 가장 가까운 픽셀 그대로 가져오는 방식이므로, 다소 부정확한 결과를 얻게된다.

  • 이중 선형 보간

  • NN 보간

3. Image resizing

• Scale Factor : 이미지의 크기를 조정할 때 사용하는 배율이다. 이를 원래 크기의 픽셀 값에 스케일 팩터를 곱해 새로운 크기를 결정한다.

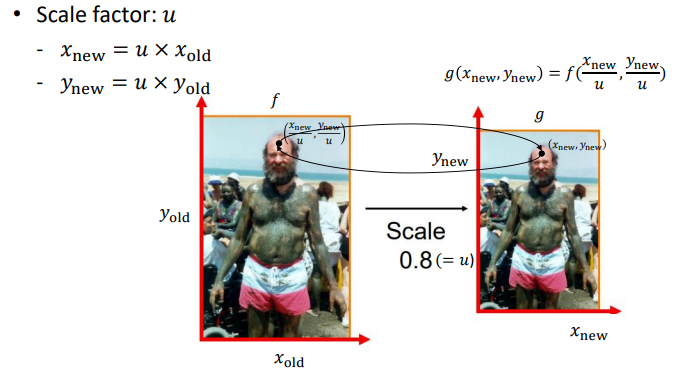
• 픽셀의 좌표에 대해

  • 각 픽셀들은 이미지 내에서 1 * 1 크기의 사각형 영역으로 간주한다.

  • 각 점들이 격자 모양으로 정렬되어 있는 것을 픽셀이라고 할 수 있다.

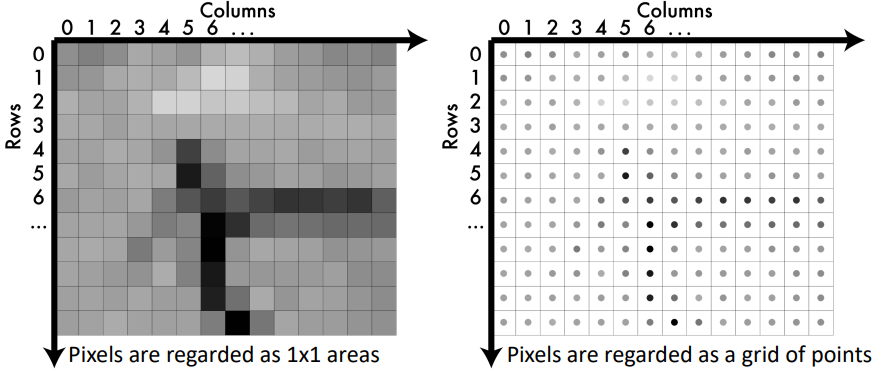
  • 픽셀들은 정수 좌표를 갖는다.

  • 픽셀의 값은 각 픽셀의 중심점에 대한 값이라고 이해할 수 있다.

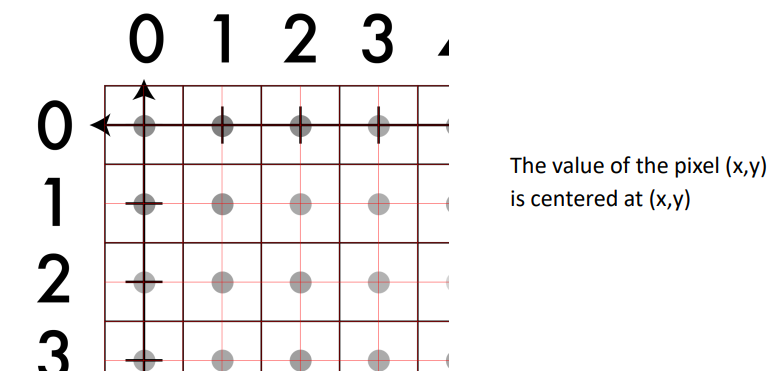
  • 하지만 실수의 좌표를 갖는 픽셀들 또한 존재한다고 볼 수 있다.

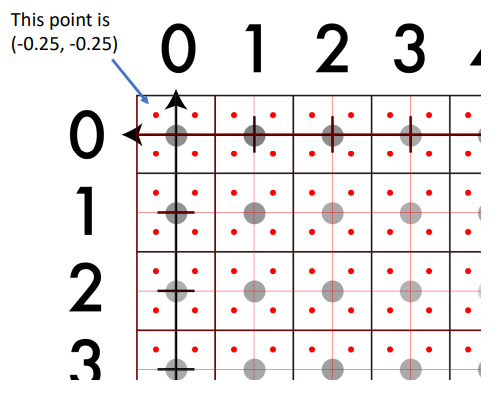
  그렇다면 우리는 비정수 좌표(실수 좌표)의 값을 어떻게 찾는가?

  답은 이중 선형 보간법에 있다. 즉, 이중 선형 보간법을 이용하면 이미지에서 정수 좌표만 갖고도 실수 좌표에 해당하는 픽셀 값들을 매칭할 수 있다.

• Image resizing : 아래 $4 * 4$ 이미지를 $7 * 7$ 이미지로 resizing (Upsampling) 하는 과정을 알아보자.

  • 새 이미지 생성 (7 * 7 size)

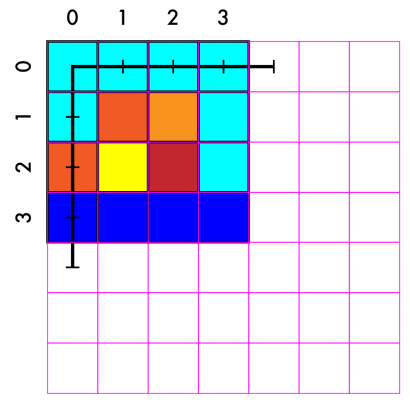
  • 새 좌표 매칭

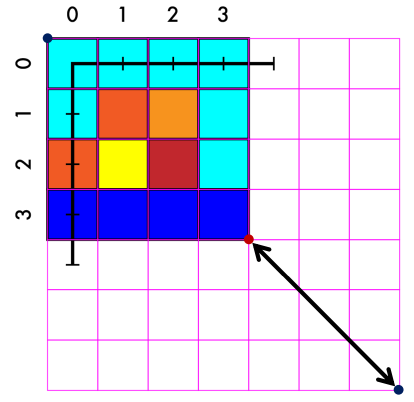
    • (-0.5, -0.5) $\rarr$ (-0.5, -0.5)

    • (3.5, 3.5) $\rarr$ (6.5, 6.5)

    $x_{old} = ax_{new} + b \\ -0.5 = -0.5a + b \\ 3.5 = 6.5a + b \\ a = \frac{4}{7},b = -\frac{3}{14} \\ \therefore x_{old} = \frac{4}{7}x_{new} -\frac{3}{14}$

  • 위에서 구한 식을 바탕으로, 모든 좌표를 매칭

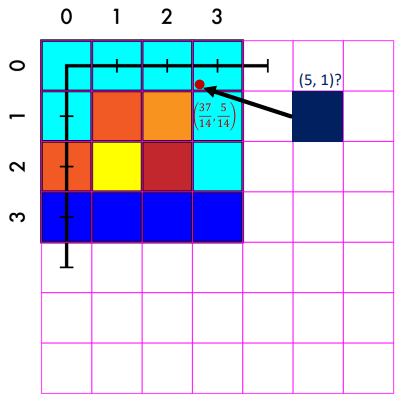
    • new point (5,1) $\rarr$ old point ($\frac{37}{14}$, $\frac{5}{14}$)

  • 결과
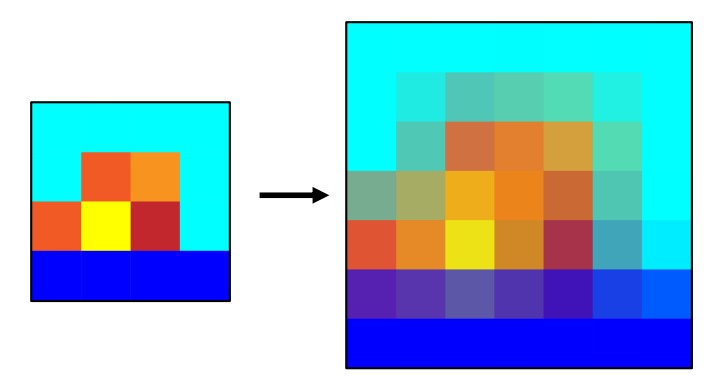