[Image Processing] Lecture 06 - Edge Detection

1. Edge Detection

• Image Edge : 이미지의 엣지는 픽셀 값(강도)이 주변 값에 비해 크게 변화하는 부분으로 정의한다. 즉, 객체의 경계선이다.

1-1. Finite Differences

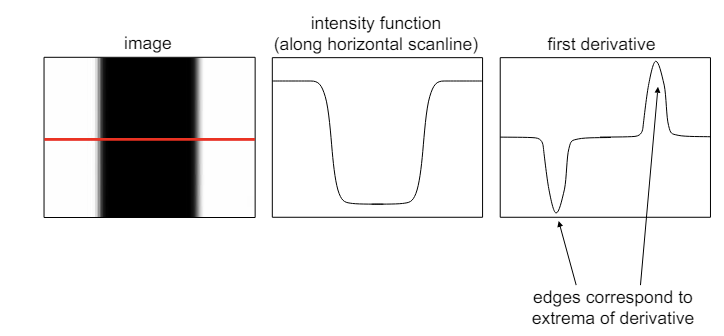
• Edge Detection : 픽셀의 가장자리를 감지하는 것은 이미지 내의 픽셀값의 급격한 변화를 찾는 것이다. 이를 위해 미분을 활용할 수 있는데, 디지털 환경에선 미분을 적용하기 어렵다. 따라서 디지털 환경에선 Finite Differences(유한 차분) 방법을 활용하여 미분을 근사한다.

• Finite Differences : 함숫값의 차이를 이용해 미분 계수를 근사하는 방법이다. 디지털 환경에서 연속 함수의 미분을 근사하기 위해 사용한다.

  • 유한 차분 식의 경우, $f(x)$와 어떤 필터간의 Convolution 연산이라고 볼 수 있다.$1*f(x+1) + 0*f(x+0) -1*f(x-1)$로 생각할 수 있는것이다. 미분 과정에서 나누기 2가 빠졌다고 해서, 변화량의 최대, 최소값에 변동이 생기지 않는다.

  • 결국, 디지털 환경에선 주변 값들의 차이를 이용해 미분에 근사하는 유한 차분 방식을 사용한다.

1-2. Sobel filter

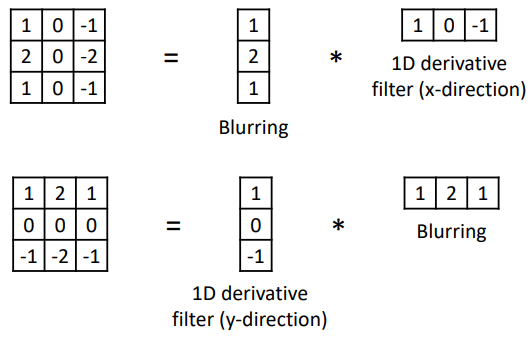
• Sobel filter : 소블 필터는 이미지의 수평 방향과 수직 방향의 픽셀값 변화율을 통해 이미지 경계를 탐지한다. 변화율이 큰 곳을 이미지의 엣지(경계)로 간주한다.

  • 블러 필터는 Noise가 Edge로 감지되는 문제를 없애는 역할을 한다.

  • 변화율 감지 필터는 유한 차분을 위한 필터이다.

  • 결국 소블 필터는 변화율 필터와 블러 필터를 합친 것으로 이해할 수 있다.

• 소블 필터의 적용

  • 이미지에 수평 커널을 적용하여, 각 픽셀에서 수평 방향의 강도 변화율을 계산.

  • 동일한 이미지에 수직 커널을 적용하여, 각 픽셀에서 수직 방향의 강도 변화율을 계산.

  • 두 밝기 변화율을 합산하여, 최종적인 엣지를 탐지한다.

    $G = \sqrt{(G_x)^2 + (G_y)^2}$

  • 우리가 관심있는 것은 변화율이기 때문에, 변화율의 절대값을 얻어내는 연산도 진행해야한다.

1-3. Image Gradient

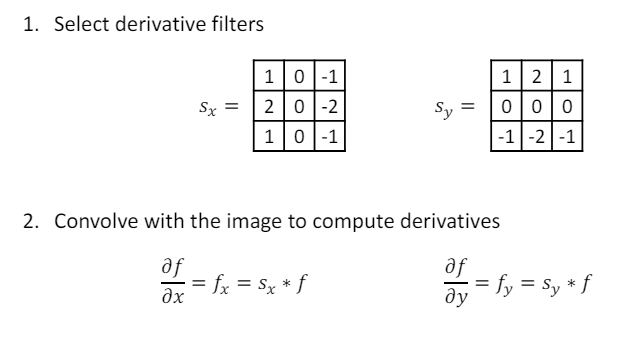
• Image gradient : 이미지의 각 지점에서 픽셀의 강도가 어떻게 변하는지 나타내는 벡터 필드이다. 이는 주로 이미지의 엣지 검출 작업에서 중요하게 사용된다.
  

  • Image gradient를 구하는 과정

    1). 이미지에서 수평 및 수직 방향의 미분을 계산하기 위한 필터를 선택한다. (Sobel, Prewitt 등등)

    2). 선택한 필터와 이미지의 Convolution 연산을 통해 수평 방향 및 수직 방향 미분값을 계산한다.

    3). 각 x, y 방향의 미분값을 이용하여 각 픽셀에서의 이미지 그래디언트를 계산한다.

• Image Gradient : 이미지에 소블 필터를 적용시킨 결과로 볼 수 있다.

• Gradient Magnitude (가장 자리의 강도) : 이미지 그래디언트의 크기는 가장자리의 강도를 나타내며, 다음과 같이 계산한다.

• Gradient Direction (가장 큰 변화율) : 이미지 그래디언트의 방향은 가장 큰 증가율의 방향을 따르며, 다음과 같이 계산한다.

• 미분 경계 필터의 문제점

  • Intensity plot (강도 플롯)
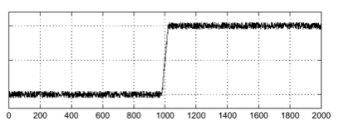
    $\rarr$ 미분 필터 적용, Derivative plot (미분 플롯)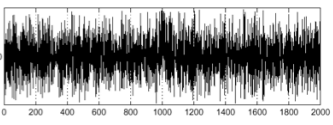

  • 위와 같은 경우에서 우리는 강도 플롯의 변화율이 큰 부분을 경계로 탐지하기를 기대하지만, 경계를 정확하지 탐지하지 못하였다.

  • 강도 플롯에 수많은 Noise가 존재하기 때문에 위와 같은 결과가 나타났다.

  • 즉, 미분 필터는 잡읍에 매우 취약하다는 것을 알 수 있다.

  • Solution : 미분 필터는 Noise에 매우 취약하기 때문에, 먼저 이미지를 흐리게(Blurring) 처리하여 노이즈를 줄인 뒤 미분 필터를 적용하는 방식을 도입하였다.

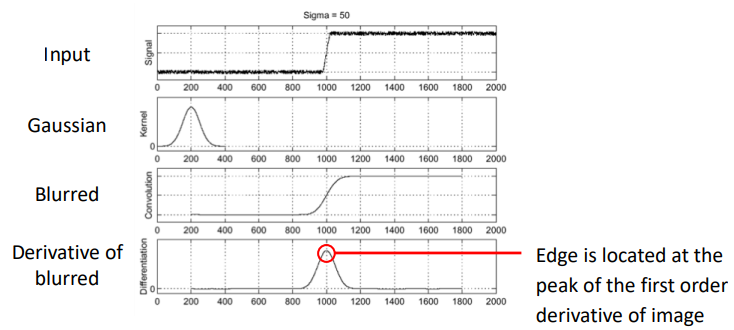
1-3. Derivative of Gaussian filter (DoG filter)

• Derivative of Gaussian filter (DoG filter) : 가우시안 함수의 미분을 직접 이미지에 적용하는 기법이다.

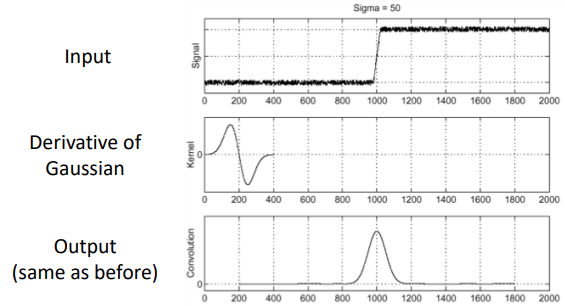
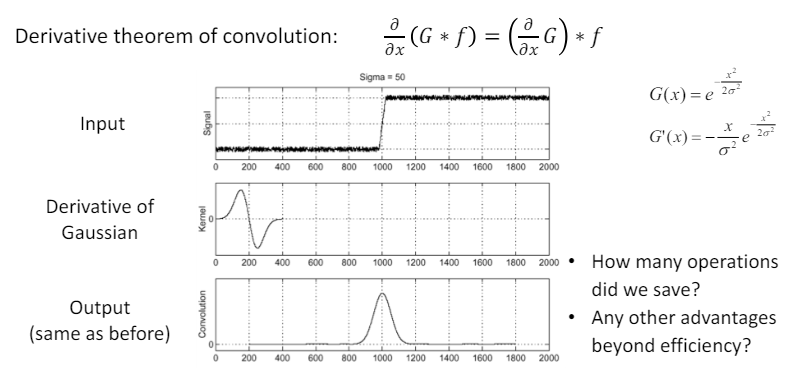
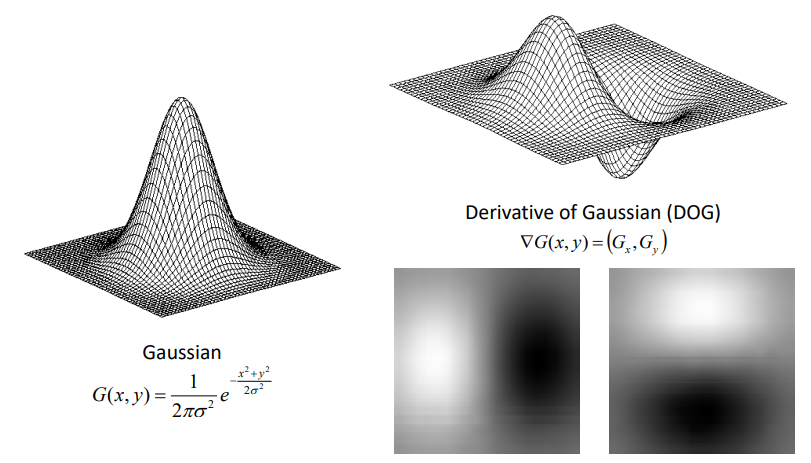
  • Derivative theorem of convolution : 컨볼루션 미분 정리는 DoG 필터의 기본 원리이다. 이 정리는 컨볼루션 연산과 미분 연산의 순서를 바꿔도 결과가 동일하다는 것을 보여준다.

• DoG 필터의 장점

  • 연산 효율성

    • 기존 방식 : 가우시안 블러를 적용하고 (1차 컨볼루션), 그 결과에 대해 미분 필터를 적용하기 때문에 (2차 컨볼루션) 2단계 연산을 거쳐야한다.

    • DoG 방식 : 가우시안 필터의 미분 필터를 이미지에 직접 적용하면 되므로, 연산을 한 번만 진행한다. 즉, 연산량이 줄어들었다.

  • 경계 탐지 : DoG 방식은 이미지의 노이즈를 감소시키므로, 경계 검출의 정확도를 향상시킨다.

2. Edge Detection - Second order derivative

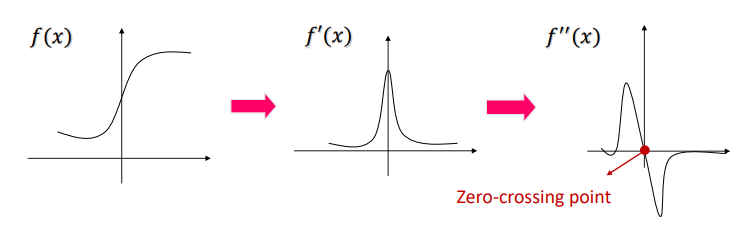
• Edge Detection : 경계 검출에서 2차 도함수를 사용하는 방법은 이미지의 강도 변화율의 변화율을 감지하여 엣지를 찾는 기법이다.

  • 이 기법은 1차 도함수의 극값이 2차 도함수의 Zero-crossing poing와 같다는 원리를 기반으로 한다. 즉, 원시함수의 변곡점을 찾아내는 것이다.

  • 2차 도함수의 변곡점 : 도함수의 값이 양에서 음으로, 음에서 양으로 바뀌는 지점이다. 이는 1차 도함수의 극값에 해당한다.

• 2차 유한 차분 : $x$방향으로 편미분을 두 번, $y$방향으로 편미분을 두 번 진행한 각 필터를 합쳐서 최종적인 필터를 생성한다. 이 필터를 Laplacian 필터라고 한다.

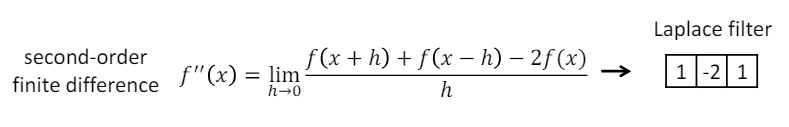
  • 위 식을 정리자면, (x, y) 위치의 픽셀 값에서 상하좌우 픽셀 값들을 모두 더한 후, 중앙 픽셀 값의 4 배를 빼는 형태로 이미지의 라플라시안 필터를 계산할 수 있다.

• 굳이 2차 도함수를 사용하는 이유?

  • 경계가 위치한 지점에서 강도의 변화율의 제일 크다. 이는 경계 픽셀의 강도 변화율의 변화율이 제일 크다는 것을 의미하고, 이런 원리를 통해 제로 크로싱이 경계의 위치를 더욱 명확히 한다는 것을 알 수 있다.
  • 2차 도함수를 사용한 경계 검출은 보통 더 얇고 정확한 경계를 생성한다. 이는 세밀한 이미지 분석에 유용하다.

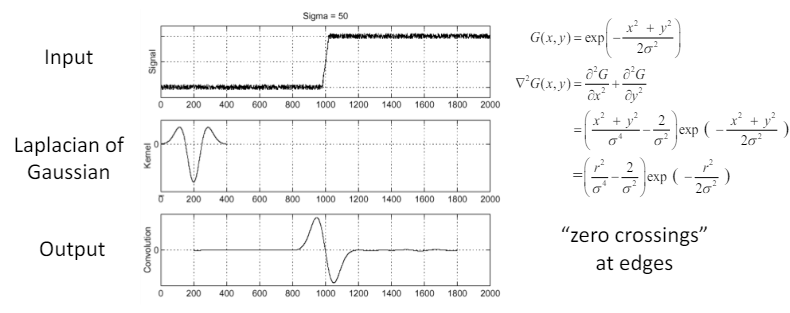
2-1. Laplacian of Gaussian filter (LoG)

• Laplacian of Gaussian filter (LoG) : 위에서 소개한 DoG 필터와 마찬가지로, 노이즈의 영향을 줄이고 경계를 더 효과적으로 탐지하기 위한 기법이다. 2차 미분한 가우시안 필터를 이미지에 적용하는 방법을 사용한다.

  • $x$에 대한 2차 편미분 가우시안 필터와 $y$에 대한 2차 편미분 가우시안 필터를 더하여 2차 미분 가우시안 필터를 생성한다.

  • 생성한 필터를 이미지에 적용하여 최종 출력 이미지를 얻는다.

  • 결과

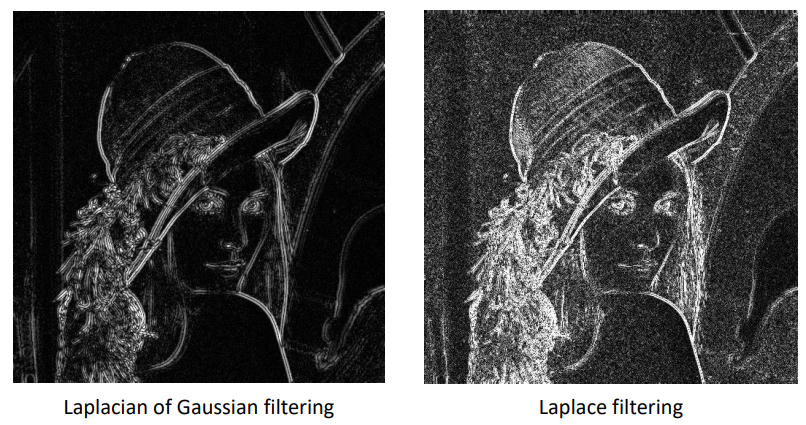
• DoG vs LoG

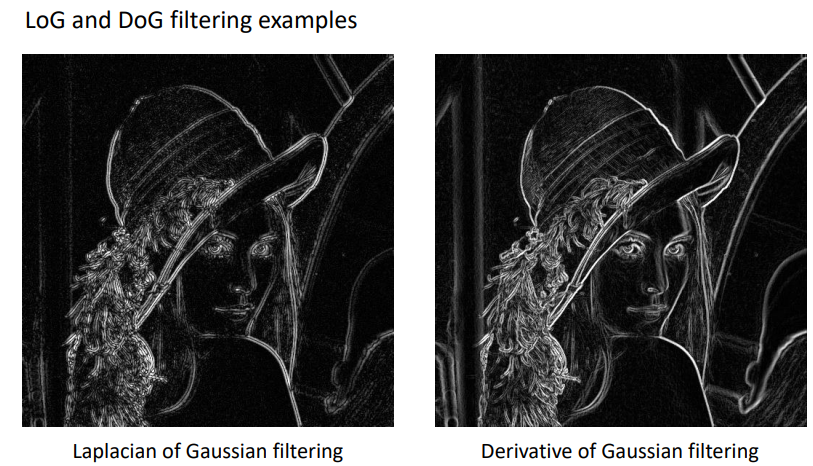
  • DoG는 변화율을 비교하여 경계를 결정하는 것에 비해, LoG는 변곡점을 기준으로 경계를 결정하기 때문에 경계 탐지 기준이 명확하다.

  • DoG는 경계를 결정하는 기준(Thread)이 필요하다.

3. Edge Detection Strategy

• Basic edge detection strategy

  1). Smoothing image for noise reduction : 이미지 스무딩으로 노이즈 줄이기

  2). Computing Image gradient to find edge candidates : Sobel 필터와 같은 미분 필터를 적용하여 이미지 그래디언트 계산 및 경계 후보 찾기

  3). Localizing edge : 이미지의 1차 미분의 극값을 찾아 엣지들을 선택

  4). Thresholding edge : 임계값을 설정하여 임계값보다 큰 그래디언트 값을 가진 픽셀만 엣지로 간주.

우리가 원하는 것은, 정확히 경계가 되는 값만 뽑아내는 것이다. 하지만 경계를 중심으로 픽셀 값들이 급격히 변하기 때문에, 변화율을 이용한 방법은 경계가 다소 두껍게 나오는 문제가 있다.

3-1. Canny edge detector

• Canny edge detector : Non-max Suppresion, Hysteresis thresholding을 통해 경계를 더 얇고 명확하게 만드는 방법.

• Non-maximum Supperssion (비최대 억제) : 경계 강도가 최대인 값만 남기고 나머지 값들을 억제하는 방법이다. 이를 통해 경계 선을 얇고 명확하게 만들고자 한다.

  • 우리의 목표는, 경계 곡선의 경계선을 얇고 명확하게 만드는 것이다.

  • 경계 곡선의 그래디언트 방향을 따라 연장선상에 존재하는 두 이웃 픽셀 사이에 보간법(선형 보간, NN 등)을 적용하여 두 이웃 픽셀과 중심 픽셀의 Gradient magnitude를 비교한다.

    • 위와 같은 경우, r을 중심 픽셀로 설정하고 양 옆에 존재하는 픽셀들과 보간법을 통해 최대값을 엣지로 결정한다.

  • 결론적으로, 경계선의 그래디언트 방향을 따라가며 정해진 크기의 윈도우를 탐색하여 더 큰 엣지 강도를 가진 픽셀만 남기는 것이다.

    • 엣지 강도 $M(x,y)$ : 찾은 이웃 픽셀들의 엣지 크기 $M(x,y)$를 비교한다. 특정 픽셀의 엣지 크기가 그 방향의 이웃 픽셀들의 엣지 크기보다 크다면 그 픽셀은 엣지라고 간주한다.

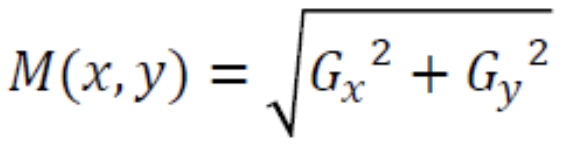
    • 엣지 방향 $A(x,y)$ : $A(x,y)$ 방향(엣지의 방향)에 있는 이웃 픽셀을 찾는다.

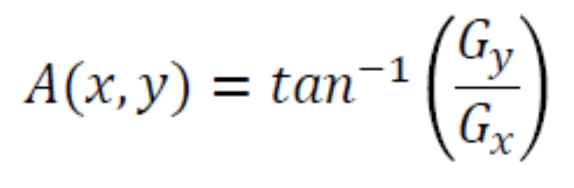
    • 위 예시의 윈도우 사이즈는 3 * 3이지만, 이 사이즈를 적절한 수준에서 더 키운다면 좀 더 명확하게 경계를 탐지할 수 있다.

  • Before vs After

불필요한 픽셀을 배제하고 확실하게 경계값에 해당하는 픽셀만 선택하기 위한 방법이라고 할 수 있다.

• Hysteresis Thresholding (Double Thresholding, 이중 임계값 처리) : 비최대 억제 방식을 통해 후보가 되는 픽셀들을 선택하였다. 픽셀의 Gradient Magnitude에 대해서 특정 값을 기준으로 분류하는 방식이다.

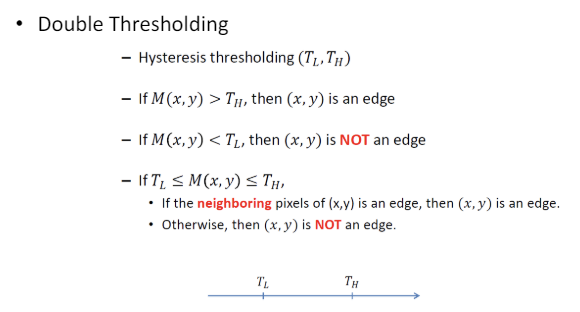
  • $M(x,y) > T_H$ (Strong Edge) : $(x,y)$는 엣지이다.

  • $M(x,y) < T_H$ : $(x,y)$는 엣지가 아니다.

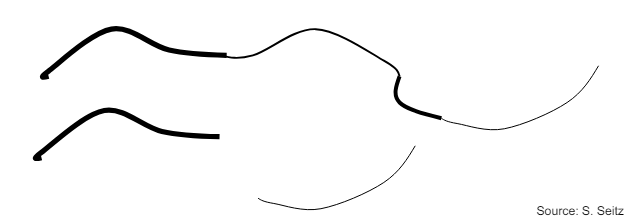
  • $T_L <= M(x,y) <= T_H$ (Weak Edge)

    • 이어지는 강한 엣지가 있는 경우 : $(x,y)$는 엣지라고 간주한다.

    • 선이 중간에 끊어지는 경우 : $(x,y)$는 엣지가 아니다.

    • 즉, 강한 엣지와 이어지는 약한 엣지는 모두 엣지로 간주되는 것이다.

  • 이중 임계값 처리 결과

• Canny edge detection 과정

  1). 이미지 스무딩

  2). 이미지 그래디언트 계산

  3). Non-maximum suppression

  4). Hysteresis thresholding

  • Canny edge detection 결과

• $\sigma$ 값 선택 (가우시안 필터)

  • 큰 $\sigma$ 값 : 가우시안 함수가 전체적으로 퍼지는 형태이므로, 전체적인 노이즈를 제거하여 전체적인 엣지 변화율을 감지하는데 유리하다.

  • 작은 $\sigma$ 값 : 가우시안 함수가 좁게 형성되므로 이미지의 세부 적인 엣지를 더욱 강조하게 된다. 노이즈까지 엣지로 감지할 가능성이 있다.