1. Binary Image
-
Segmentation (세분화) : 세분화는 주어진 데이터를 의미 있는 부분으로 나누는 과정이다. 이미지 처리에서 이는 일반적으로 이미지 픽셀을 객체와 배경으로 분류하는 것을 의미한다.

-
Binary Image (이진 이미지) : 이진 이미지는 모든 픽셀이 0 혹은 1로 표현되는 이미지로, 0은 백색(Background), 1은 흑색(Foreground)을 나타낸다.
-
Neighborhoods
-
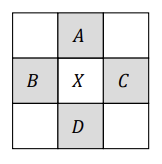
4-Neighborhood () : {A,B,C,D}는 주어진 픽셀 X에 대해 이다. 즉, 인접한 4개의 픽셀만 이웃으로 취급.
-
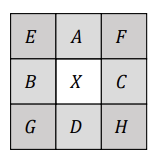
8-Neighborhood () : {A,B,C,D,E,F,G,H}는 주어진 픽셀 X에 대해 이다. 즉, 인접한 4개의 픽셀과 대각선 4개의 픽셀 모두 이웃으로 취급.
-
-
Connectedness (연결성) : 픽셀들이 어떻게 연결되어 있는지를 정의하는 개념.
-
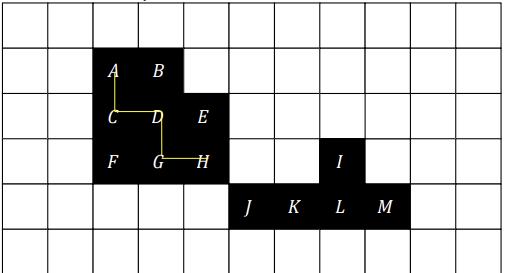
4-Neighborhood
-
A와 H는 연결되어있다.
-
A와 K는 연결되어 있지 않다.
-
{A,B,C,D,E,F,G,H}은 연결된 구성 요소 집합이다.
-
{I,J,K,L,M}은 연결된 구성 요소 집합이다.
-
총 두 개의 연결 집합으로 구성된다.
-
-
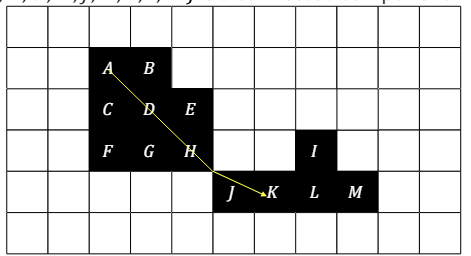
8-Neighborhood
-
A와 H는 연결되어 있다.
-
A와 K도 연결되어 있다.
-
{A,B,C,D,E,F,G,H}는 연결 구성 요소의 집합이 아니다. 연결 집합은 가능한 모든 구성 요소가 존재해야한다.
-
{A,B,C,D,E,F,G,H,I,J,K,M}은 연결된 구성 요소 집합이다.
-
-
-
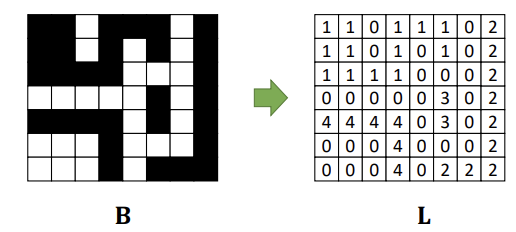
Connected Components Labeling (연결 요소 레이블링) : 이진 이미지에서 서로 연결된 픽셀 집합을 식별하고, 각 집합에 고유하며 동일한 레이블을 할당하는 작업이다.
-
각 픽셀에 대해 4-Neighborhood이든 8-Neighborhood이든 선택된 연결성을 사용하여 연결된 모든 픽셀을 탐색한다.
-
현재 픽셀이 배경(일반적으로 0)이면 탐색을 건너뛰고, 그렇지 않으면 새로운 레이블을 할당한다.
-
연결된 모든 픽셀은 동일한 레이블을 할당받는다.
-
-
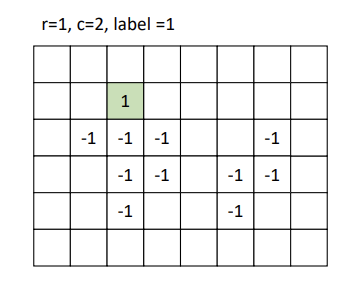
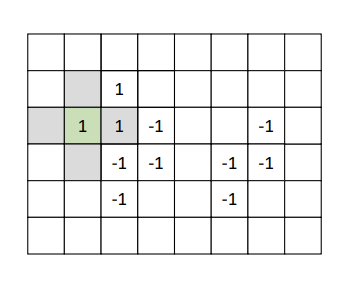
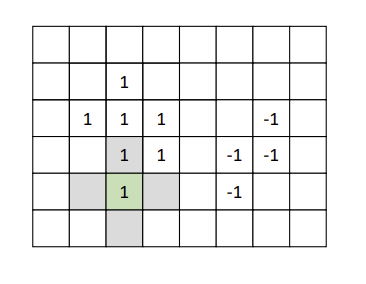
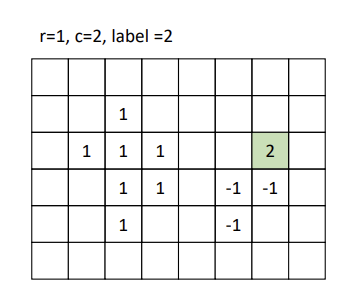
Recursive Labeling : 픽셀 간의 연결성을 탐색할 때 재귀적으로 호출하는 방법.
-
이진 이미지의 각 픽셀을 검사하여 아직 레이블이 할당되지 않은 픽셀을 찾는다.
-
현재 픽셀에서 시작하여 연결된 모든 픽셀을 재귀적으로 탐색한다.
-
위 과정을 재귀적으로 반복한다.
-
-
레이블링이 중요한 이유

-
객체 식별 및 분할 : 서로 연결된 픽셀 집합을 식별하고 구분하는 과정에서 개별 객체를 독립적으로 분석하고 처리할 수 있다.
-
특징 추출 : 각 객체의 특징을 보다 쉽게 추출할 수 있다.
-
이미지 분석 및 이해 : 이미지 내에 몇 개의 객체가 존재하는지, 각 객체는 어떤 특징이 있는지 등을 파악할 수 있다.
-
관리 용이성 : 레이블링된 이미지는 각 객체를 개별적으로 조작하거나 분석하는 데 용이하다.
-
2. Morphological processing
-
Basic Operations
-
Translation
-
Dilation
-
Erosion
-
Closing
-
Opening
-
2-1. Translation
- Translation (이동) : 이진 이미지에서 특정 위치 벡터만큼 픽셀 집합을 이동시키는 연산이다. 픽셀 집합 를 위치 벡터 만큼 이동시킨 결과는 다음과 같다.
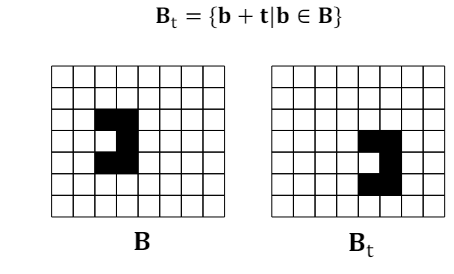
2-2. Dilation
-
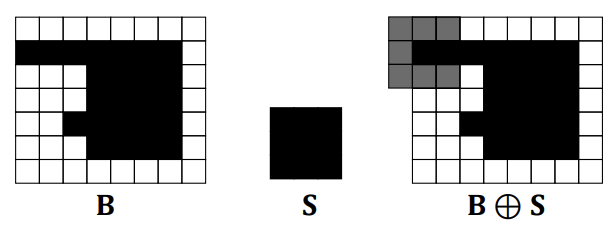
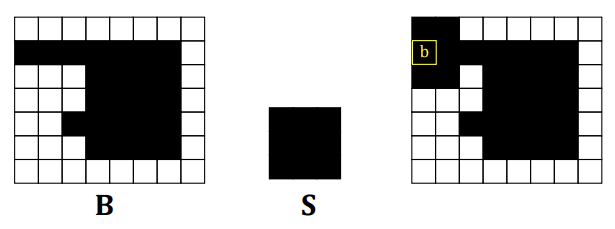
Dilation (팽창) : 객체의 경계를 확장하여 객체를 더 크게 만드는 연산이다. 이는 객체 내의 작은 구멍을 채우거나 근접한 객체들을 연결하는 데 사용된다.
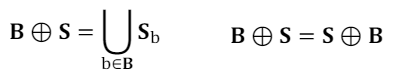
-
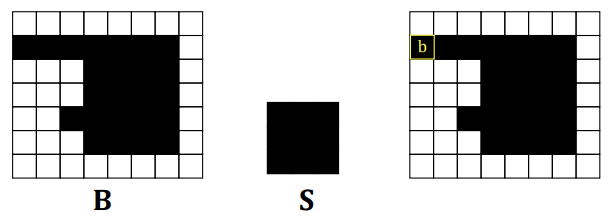
이진 이미지 B에 대해 구조 요소 S에 의한 팽창은 위와 같다.
-
구조 요소 S가 B의 각 검은 픽셀 위에 위치할 때, 구조 요소에 의해 커버되는 모든 위치에 있는 픽셀들은 평창 결과의 일부가 된다.
-
이 과정을 거치며 객체는 더 커지게 된다.

-
2-3. Erosion
-
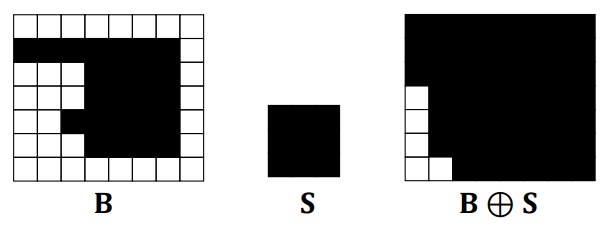
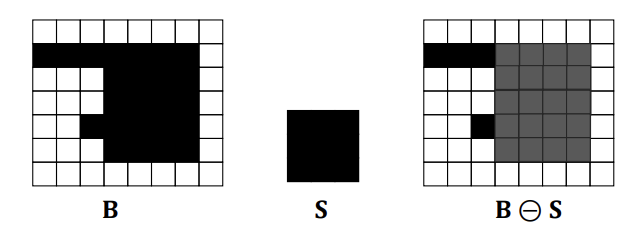
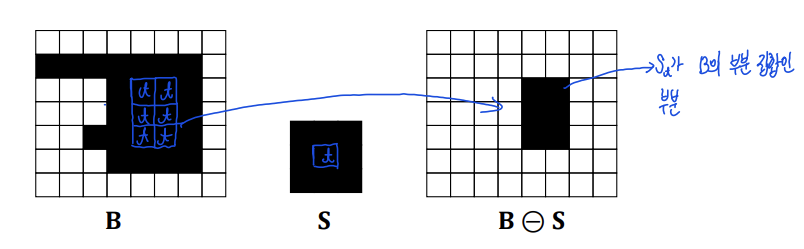
Erosion (침식) : 객체의 경계를 축소하여 객체를 더 작게 만드는 연산이다. 이는 작은 객체나 노이즈를 제거하는 데 유용하다.
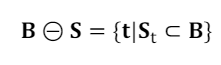
-
가 의 부분집합일 때, 의 중심인가 연산의 결과로 남게 된다.
-
침식 연산의 결과로, 객체가 전체적으로 줄어든다.
-
몇몇 격리된 픽셀들이 제거될 수 있는데, 이는 노이즈 감소의 효과가 있다.
-
2-4. Opening and Closing
-
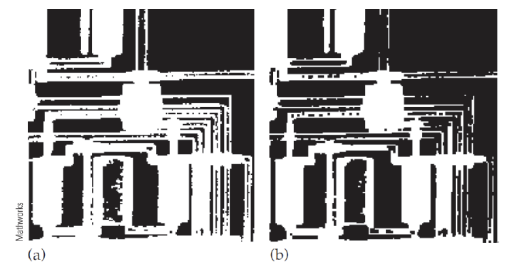
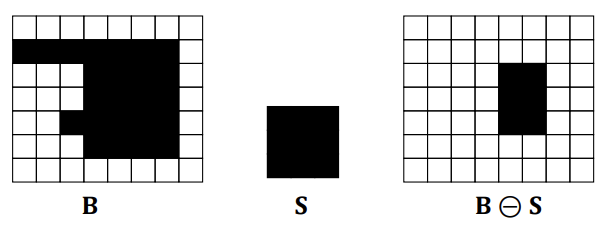
Opening : 침식 후 팽창을 적용하는 연산이다. (Erosion Dilation)

-
수학적 표현은 다음과 같다.
-
Idempotence : Opening 연산은 한 번을 초과해서 수행할 수 없다.
-
연산 결과, 노이즈나 얇은 돌기가 제거되고 객체를 더 작게 만들어 객체들 사이의 작은 틈을 분리하여 객체를 보다 선명하게 만든다.
-
Erosion vs Opening
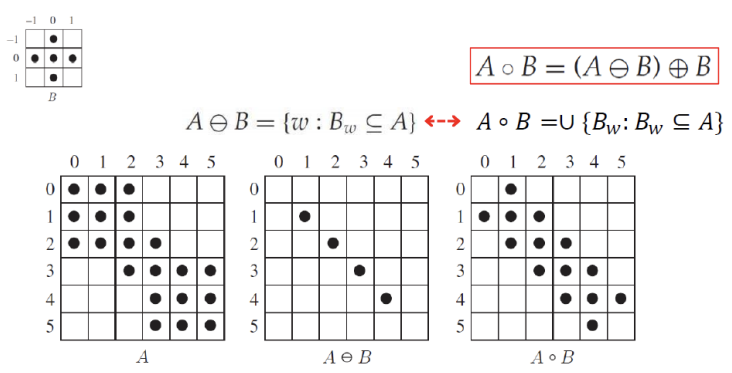
-
-
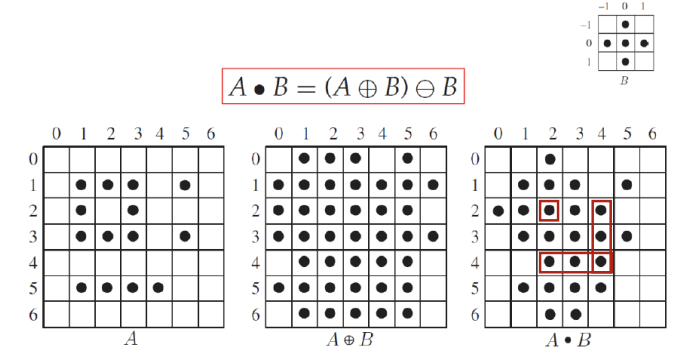
Closing : 팽창 후 침식을 적용하는 연산이다.(Dilation Erosion)
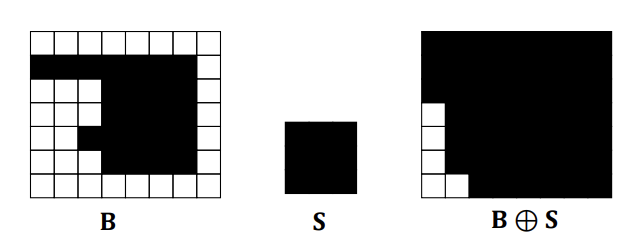
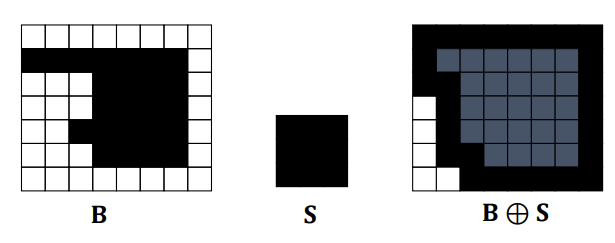
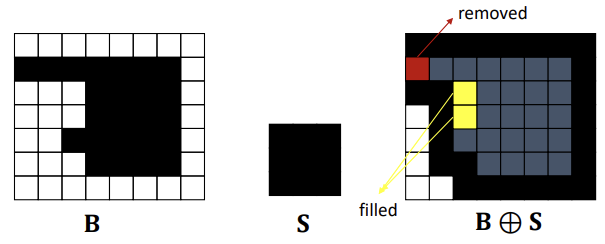
-
수학적 표현은 다음과 같다.
-
연산 결과, 작은 구멍이나 간격을 채우고, 전체적인 형태를 보존하면서 객체의 경계를 보다 명확히 한다.
-
Idempotence : Closing 연산은 한 번을 초과해서 수행할 수 없다.
-
Dilation vs Closing
-
-
Opening vs Closing
-
Opening
-
이미지 스무딩
-
얇은 선 끊어내기
-
작은 객체 (노이즈) 제거
-
-
Closing
-
이미지 스무딩
-
작은 공간 채우기
-
작은 객체 (노이즈) 제거
-
-
-
Opening Closing : Opening 과정에서 노이즈를 제거하고 생기는 구멍들을 Closing을 통해 채워준다. 서로의 단점을 상쇄시키는 방법.
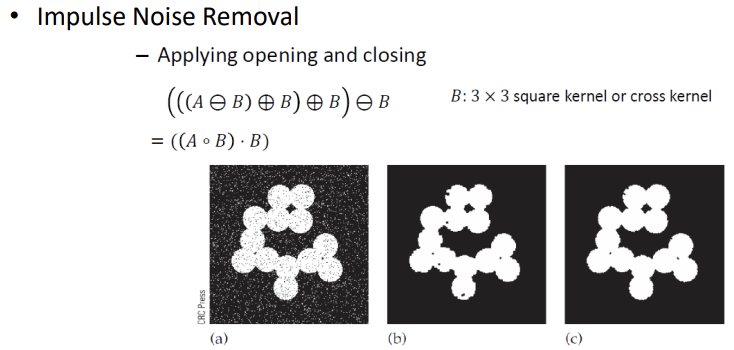
2-5 Morphological Processing
-
Edge Detection by Dilation and Erosion
-
이진 이미지에서 경계 검출을 수행할 때, 팽창과 침식 연산을 사용할 수 있다.
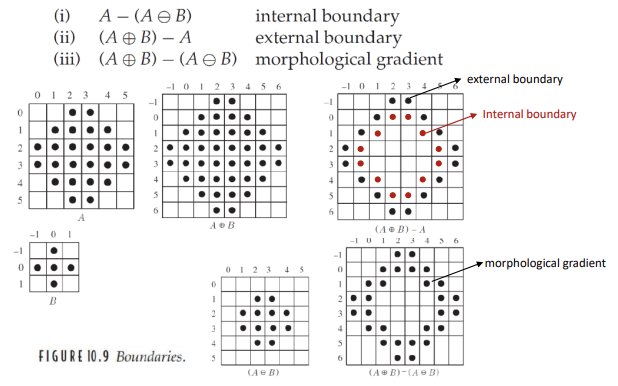
1). 원본 이미지와 침식 이미지의 차이를 이용 : 이 방식을 통해 객체의 내부 경계를 잘 드러낼 수 있다.
2). 팽창 이미지와 원본 이미지의 차이를 이용 : 이 방식을 통해 객체의 외부 경계를 잘 드러낼 수 있다. 이때, 팽창으로 인해 경계가 더 두꺼워질 수 있다.
3). 팽창 이미지와 침식 이미지의 차이를 이용 : 이 방식을 통해 이미지의 경계를 더 세밀하게 드러낼 수 있다.

-
