[Image Processing] Lecture 08 - Thresholding

1. Segmentation

• Segmentation : 이미지를 비슷한 정보를 가진 비중첩 영역(객체)으로 나누는 과정이다. 이를 통해 이미지 내의 다양한 객체를 식별하고 분리하여 다양한 정보를 얻을 수 있다.

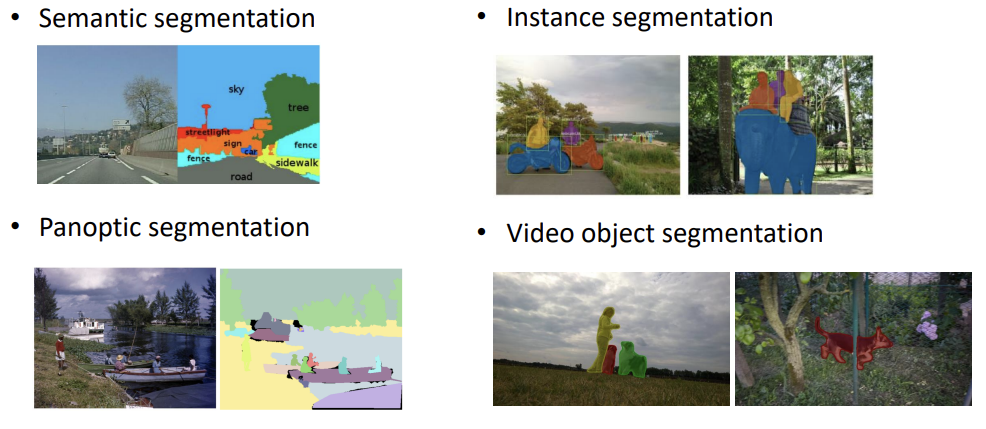
• Segmentation Method

  • K-means clustering

  • Mean Shift

  • Normalized-cut

  • Graph cut

  • Random-walk

  • Markov random field (MRF) optimization

• Image Thresholding (이미지 임계값 처리) : 이미지를 분할하는 기법. 특정 임계값을 기준으로 이미지를 두 개의 그룹(Foreground, Background)으로 분리한다. 이 방법은 주로 Gray scale 이미지에 적용된다. 이미지의 숨겨진 부분도 추출이 가능하다.

  • Single thresholding (단일 임계값 처리) : 전체 이미지에 대해 하나의 고정된 임계값을 적용한다. 이 방법은 이미지의 전반적인 밝기가 균일할 때 유효하다.

  • Double thresholding (이중 임계값 처리) : 두 개의 임계값을 사용하여 각 객체를 더욱 세밀하게 분리하는 방법.

  • Otsu's thresholding : 자동으로 임계값을 계산하는 방법으로, 이미지의 히스토그램을 분석하여 최적의 임계값을 찾는 방법. 이는 두 개의 피크(예를 들면, 전경과 배경) 사이의 분산을 최대화하는 임계값을 선택한다.

2. Thresholding

• 적절한 임계값 예측하기 : 임계값을 결정하기 위해서는 이미지의 히스토그램을 관찰하는 것이 중요하다. 히스토그램은 이미지의 밝기 분포를 보여주며, 대개 전경과 배경을 나타내는 두 개의 주요 분포가 있다. 적절한 임계값은 이 두 분포 사이에 위치해야한다.

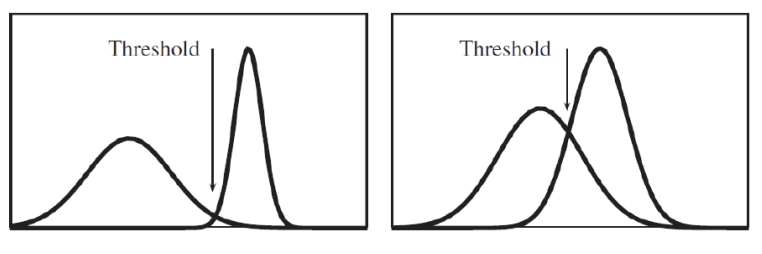
2-1. Otsu's Method

• Otsu's Method : 이미지를 배경과 객체를 분리할 때, 클래스 내 분산을 최소화하고 클래스 간 분산을 최대화하는 임계값을 찾는 알고리즘이다. 이 방법은 특히 두 개의 주요 분포를 가진 이진 신호 분석에 적합하다.

  • 클래스 내 분산 최소화 : 한 클래스에 속한 픽셀들은 비슷한 값을 가져야 잘 그루핑했다고 볼 수 있다. 즉, 클래스 내 분산은 작을수록 좋다.

  • 클래스 간 분산 최대화 : 두 그룹으로 나누어진 픽셀들은 서로 차별점이 클수록 좋다. 즉, 그룹간 분산은 클수록 좋다.

  • 분산의 관계 : 이진 신호에서 전체 분산은 클래스 내 분산과 클래스 간 분산의 합과 같다. 따라서, 클래스 간 분산을 최대화하는 것은 클래스 내 분산을 최소화하는 것과 동일한 결과를 가져온다.

  • 즉, 오츠의 메소드는 k값을 바꿔감에 따라 두 개의 그룹이 달라지고, 분산도 당연히 달라진다. 이를 반복하며 가장 적절한 k값을 결정하는 방법이다.

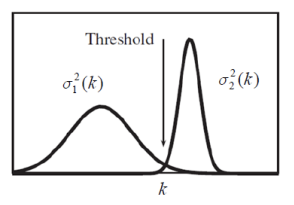
  • The following properties

    • M * N 크기의 이미지

    • L(256)개의 픽셀 값(이 경우 0 ~ 255, 8bit)을 가짐

    • 밝기 $i$값을 갖는 픽셀의 수는 : $n_i$

    • 밝기 $i$를 갖는 픽셀의 비율 : $p_i = \frac{n_i}{MN}$

    • 모든 L에 대한 이 비율의 합 : $\sum_{i=0}^{L-1}p_i = 1$

    • 임계값 k에 의해 두 개의 그룹으로 나누어지고, k는 어느 그룹에 속해도 상관 없지만, 그룹 1에 속한다고 가정.

      $C_1 \rarr [0,k], C_2 \rarr [k+1, L-1]$

      

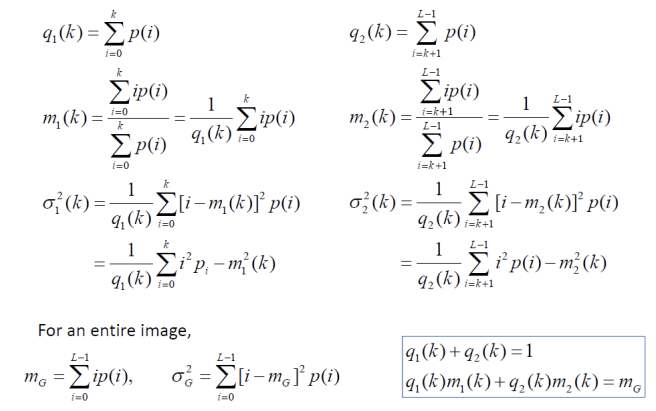
    • $q_1(k), q_2(k)$는 임계값 k전 후 범위의 모든 $p(i)$의 합으로, 클래스 간 비율을 나타낸다.

    • $m_1(k), m_2(k)$는 각각의 영역의 평균 밝기를 나타낸다.

    • $ip(i)$는 가중 평균을 의미한다.

    • ${\sigma_1}^2(k), {\sigma_2}^2(k)$는 각 영역 내에서 밝기 값의 분산을 나타낸다.

    • $m_G, {\sigma_G}^2$는 각각 이미지 전체에 대한 평균과 분산이다.

• 최적의 임계값 찾기 : 클래스간 분산이 최대가 되는 k를 찾는 것이다.

• 클래스간 분산 재귀적 계산 : $0$ ~ $k$까지 범위에 대한 평균을 구하였을 때, 편하게 계산하는 방법

  • $q_1(0) = p_0, m_1(0) = 0$이다.

  • Moving Average 방식으로 계산할 수 있다.

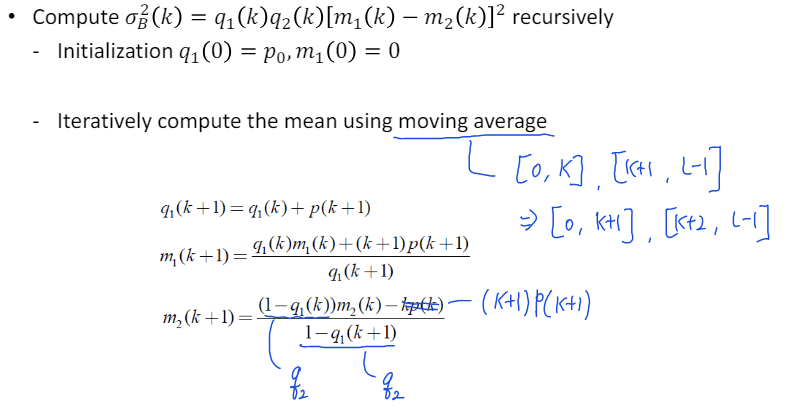
2-2. Adaptive thresholding

• Adaptive thresholding (적응 임계값 처리) : 전체 이미지에 대해 단일 임계값을 사용하는 기존의 임계값 처리 방법의 한계를 극복하기 위해 고안된 방법.

  • 이미지를 일련의 하위 이미지 또는 구역으로 나누고, 각 하위 이미지에 대해 별도의 임계값을 적용한다.

  • 이 방법을 통해, 각 하위 이미지의 특성에 맞는 임계값을 결정하여, 더 정밀한 이미지 처리가 가능해짐.