[Image Processing] Lecture 09 - Image Restoration

1. Image Restoration

• Image restoration : 이미지가 겪은 품질 저하를 줄이는 과정이다. 즉, 원본 이미지가 가지고 있던 선명도나 상세 내용을 최대한 복구하는 것이다.

1-1. Image Degradation

• Image Degradation (이미지 품질 저하) : 여러가지 요인(Noise, Out-of-focus blur, Motion blur 등)으로 인해 이미지의 품질 저하가 발생하는 현상.

• Model of Image Degradation (이미지 열화 모델) : 입력된 열화 이미지 $g(x,y)$가 주어졌을 때, 원본 이미지 $f(x,y)$를 추정하기 위해 이미지 열화 과정을 수학적으로 모델링하는 것.

  • 기본적인 이미지 열화 모델은 다음과 같이 표현할 수 있다.

    $g(x,y) = f(x,y) * h(x,y) + n(x,y)$

  • $n(x,y)$ : 추가적인 노이즈

  • $h(x,y)$ : 블러링 커널 (필터링 마스크)

  • $*$ : Convolution 연산

• Noise : 외부 요인으로 인해 이미지가 열화되는 모든 종류의 현상이다.

  • 노이즈의 종류

    • Salt and Pepper Noise : 이미지에 흰색과 검은색 픽셀이 무작위로 발생하는 노이즈. 주로 디지털 이미지에서 발생한다.

    • Gaussian Noise : 노이즈가 정규 분포를 따르는 경우. 주로 전자 기기에서 발생하는 열로 인해 발생.

    • Speckle Noise : 주로 레이더 및 의료 영상에서 발생하며, 점 모양의 패턴으로 나타난다.

    • Periodic Noise : 주기적으로 발생하는 노이즈로, 주로 전기적 간섭에 의해 발생.

  • Noise 모델을 보다 단순화 하기 위해 $g(x,y) = f(x,y) + n(x,y)$이라 가정하자.

2. Salt and Pepper Noise

• Salt and Pepper Noise : 이미지에서 예상치 못한 방해로 인해 발생한다. 마치 소금과 후추가 뿌려진 것처럼, 이미지에 무작위로 흰색 또는 검은색 픽셀로 나타난다.

  • The Solution - Median Filtering : 주변 픽셀들의 값을 순서대로 나열한 후 중앙 값을 선택하여 현재 픽셀의 값을 대체하는 방법(주로 Rank-Order Filtering을 사용). 매우 효과적인 해결 방법이다.

• Median Filtering (중앙값 필터링) : 소금-후추 노이즈를 제거하는데 매우 효과적인 필터링 기법이다.

  • 위와 같이 노이즈가 발생한 경우, 평균 필터 등의 방법을 적용한다면 255라는 노이즈가 다른 픽셀들에게 큰 영향을 미치게 된다.

  • 따라서 윈도우 내 모든 픽셀 값들을 나열한 후, 중앙값을 선택하는 것이 더 나은 해결 방법이라고 볼 수 있다.

  • 결과

3. Gaussian Noise

• Additive White Gaussian Noise (AWGN) : 이미지 처리 및 통신 시스템에서 자주 발생하는 노이즈 유형이다.

  • 주로 원본 이미지에 노이즈를 더한 형태로 나타난다. 즉, $I_G(x,y) = I(x,y) + N(x,y)$

  • White Noise : 무작위로 발생하고 정규 분포를 따른다.

  • 대부분의 가우시안 Noise는 AWGN을 가정한다.

  • 보통, 평균이 0인 AWGN을 가정하는데, 노이즈의 평균이 0이라는 것은 노이즈가 이미지의 밝기를 높이거나 낮추지 않는다는 것을 의미한다.

  • 분산이 클수록 노이즈가 많아지고, 분산이 작을수록 노이즈가 적어지는 특징이 있다.

• Average Filter (평균 필터) : 가우시안 노이즈를 없애는 데 가장 효과적인 방법이다.

  • 노이즈가 있는 이미지 $I_G$가 100개가 있다고 가정해보자.
    ${I_G}^i(x, y) = I(x, y) + N^i(x, y), \\i = 1, … , 100$

  • $I_G$에 대한 평균을 내면 다음과 같다.
    $\frac{1}{100}\sum_{i=1}^{i=100}{I_G}^i(x,y) = I(x,y) + \frac{1}{100}\sum_{i=1}^{i=100}N^i(x,y)$

  • $\frac{1}{100}\sum_{i=1}^{i=100}N^i(x,y)$ : AWGN에서 평균은 0으로 가정하므로, 이 값은 0에 근사한다.

  • 결론적으로, AWGN 노이즈가 추가된 이미지를 모아놓고 전체 이미지에 대한 평균을 계산하면 노이즈는 평균적으로 감소하고 원본 이미지가 보존된다.

3-1. Simple Average Filtering

• Simple Average Filtering : 이번엔 오직 1개의 Noisy Image만 갖고 있다고 생각해보자.

  • 평균 필터링을 통해 존재하는 노이즈들을 전체적으로 모은다고 생각해보자.

  • 우리는 가우시안 노이즈의 평균을 0으로 가정하였다.

  • $5 * 5$ 필터로 진행했다면, 25개의 노이즈를 모은 것이다.

  • &11 * 11$ 필터로 진행했다면, 121개의 노이즈를 모은 셈이다.

  • 모인 노이즈가 많아질수록, 평균했을 때 노이즈의 값을 0에 가깝게 만들 수 있을것이다.

  • 결국, 필터의 크기는 매우 중요한 문제이다.

    • Small size window : 작은 크기의 Window는 노이즈 제거에 효과적이지 않다.

    • Large size window : 큰 크기의 Window는 노이즈 제거에 효과적이지만, 이미지가 과하게 Blurring 된다.

• 필터링 결과
  

3-2. Adaptive Filtering

• Wiener filter : 이 필터는 이미지의 지역적 특성에 따라 필터의 특성을 적응적으로 변경한다. 즉, 노이즈를 제거하면서도 이미지의 특징을 잃지 않기 위한 기법이다.

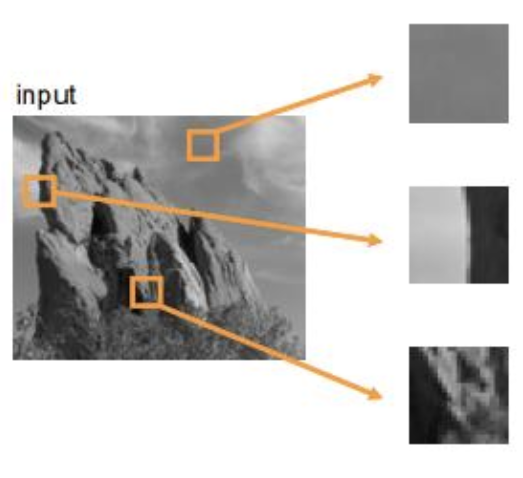
  • 어느 지점이 어떤 특징(uniform, edge 등)을 갖고 있는지 알 수 있는 제일 간단한 지표는 분산이다.

  • 분산이 크다면, 주변 픽셀과 차이점이 큰 픽셀이라는 뜻이므로, 오브젝트의 경계일 확률이 높다.

  • 분산이 작다면, 주변 픽셀과 비슷한 픽셀이라는 뜻이므로, Uniform한 픽셀일 것이다.

  • 따라서 평균 필터를 적용할 때, 지역의 특징에 맞게 가중치를 두어 계산하는 방식을 사용한다.

• Wiener filter 동작 과정

  • $m(x,y)$ : (x,y)위치의 픽셀에서 마스크의 평균 강도값을 나타낸다.

  • ${\sigma_f}^2$ : 마스크 내의 픽셀 값들의 분산을 나타낸다.

  • $I_G(x,y)$ : 이미지의 (x,y)위치에서의 픽셀 강도(밝기) 값을 나타낸다.

  • ${\sigma_N}^2$ : 이미지 전체의 분산을 나타낸다.

  • High ${\sigma_f}^2$ : 경계가 위치한 영역으로 인식.

  • Low ${\sigma_f}^2$ : 경계가 위치하지 않은, 평활화된 지역으로 인식.

즉, 적응형 필터 방식은 노이즈를 효과적으로 제거하면서도, 이미지의 특징을 보존할 수 있다는 장점이 있다.

• 결과

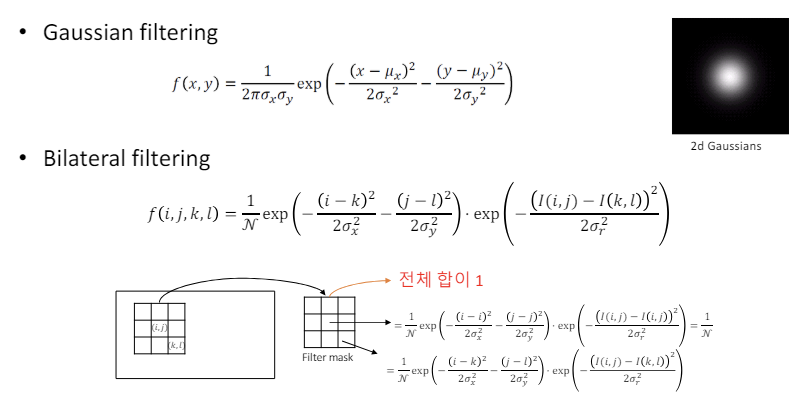
• Bilateral filter (양방향 필터) : 이 필터는 Wiener filter와 마찬가지로, 이미지의 특징(엣지)을 보존하면서 노이즈를 제거하기 위한 기법이다. 이 방식은 공간적 가중치와 강도 가중치를 동시에 고려하여 계산한다.

  • 공간적 가중치 (Spatial Weight) : 픽셀 간의 공간적 거리에 기반하여 계산된다. 가까운 픽셀은 더 높은 가중치를 받고, 멀리 떨어진 픽셀은 낮은 가중치를 받는다.

  • 강도 가중치 (Intensity Weight) : 이 가중치는 픽셀 간의 강도(밝기) 차이에 따라 계산된다. 비슷한 밝기를 가진 픽셀은 더 높은 가중치를 받고, 밝기 차이가 큰 픽셀은 낮은 가중치를 받는다.

• Bilateral filter vs Gaussian filter

  • 가우스 필터는 픽셀의 중심에 가까울수록 해당 픽셀에 가중치를 더 높게 주는 방식.

  • 양방향 필터는 픽셀의 중심에 대한 거리 뿐만 아니라 픽셀 강도의 차이도 고려하여 가중치를 계산하는 방식이다.

3-3. Nonlocal Means Filtering

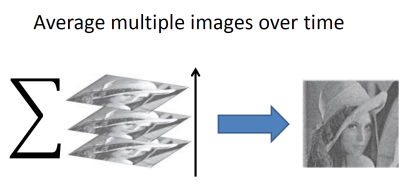
• Nonlocal Means Filtering (NLM) : Noisy Image를 모아놓고 평균을 구하면, 노이즈는 제거하고 원본 이미지에 가깝게 복원할 수 있다. 이런 방식으로 노이즈를 제거하는 기법이다.

  • 동작 방식

    • 한 이미지의 블록을 모든 이미지 블록의 가중 평균으로 대체한다.

    • 유사한 블록일수록 더 큰 가중치를 부여한다.