오늘 공부해 볼 주제는 해시 테이블이다.
해시테이블 (Hash Table)이란?
해싱을 통해서 데이터를 저장하는 자료구조다.
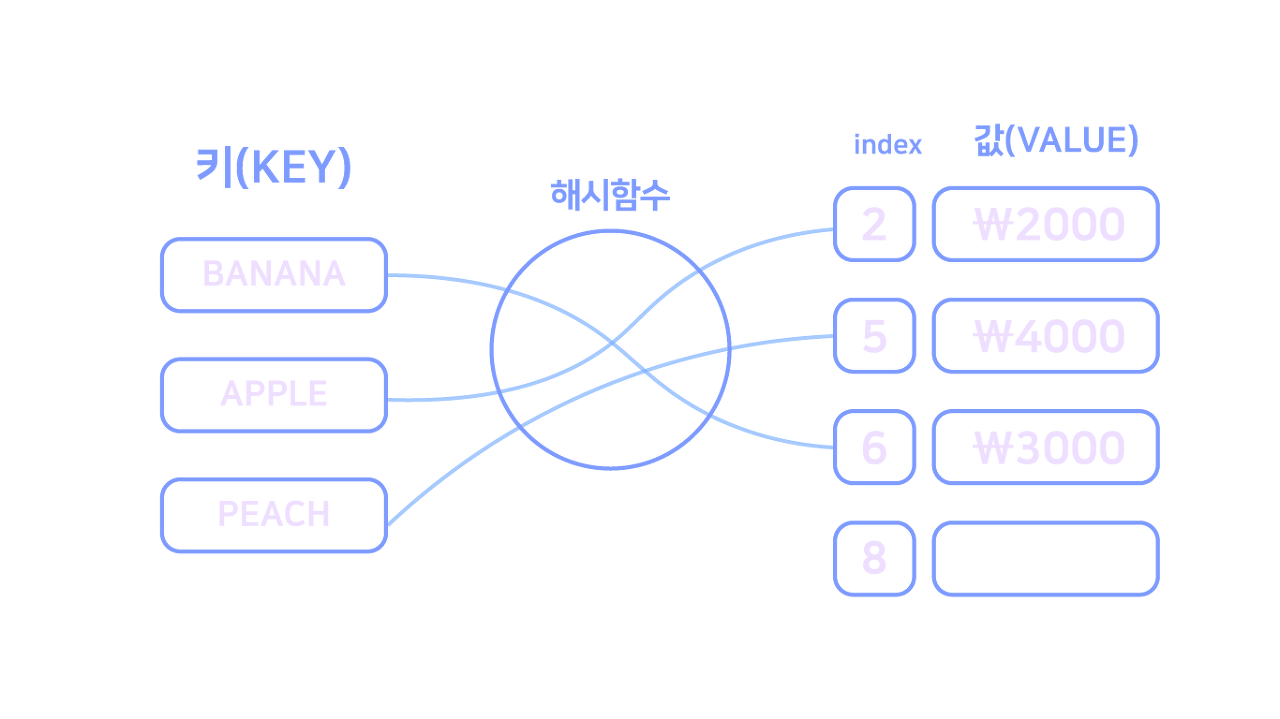
즉, 해시 함수를 사용해서 변환한 값을 색인(index)로 사용해 키(key)와 데이터(값, value)를 저장하는 자료구조 이다.
이때 실제 값이 저장되는 장소를 버킷이라고 한다.
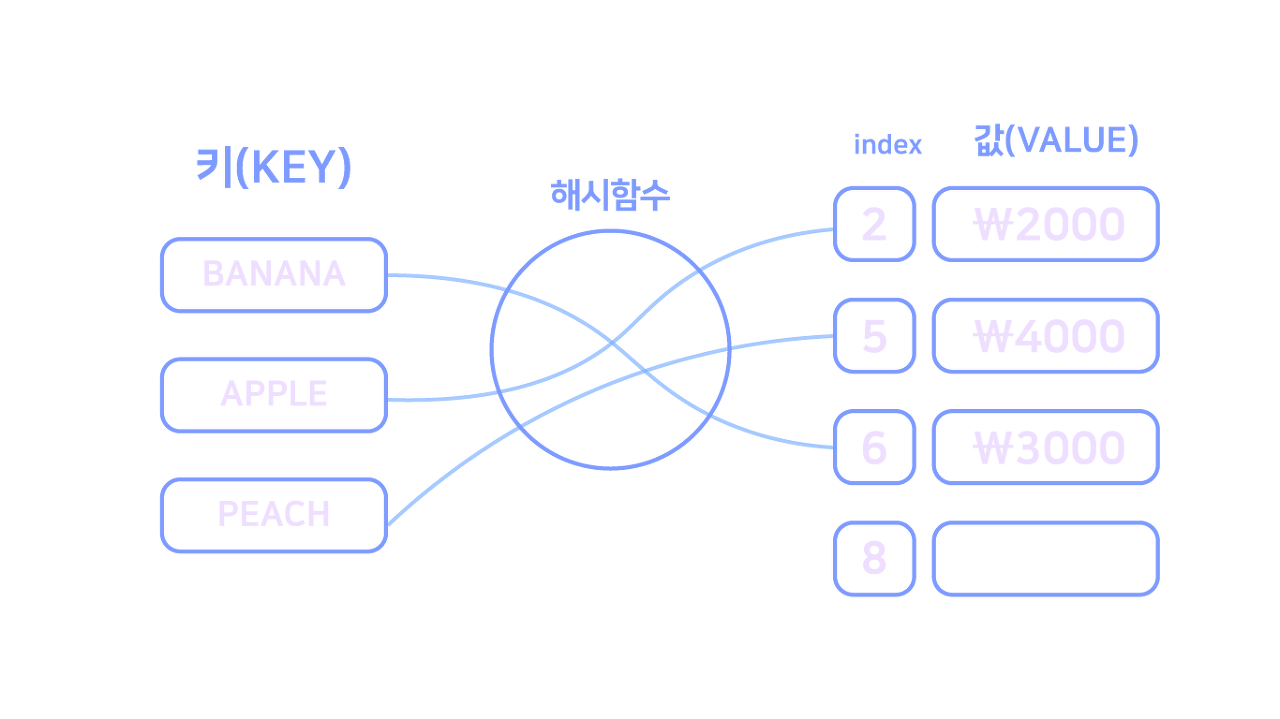
이렇게 키를 해시 함수에 넣어 반환된 값을 배열의 인덱스로 사용해서
해당 인덱스에 데이터를 저장하는 식으로 동작한다.
단점
-
순서를 보장하지 않기 때문에, 순서, 관계가 있는 목적에는 적합하지 않다.
-
데이터가 pseudo-random 위치에 저장되기 때문에 데이터를 정렬된 순서로 접근할 때 비용이 높다.
-
loop하면서 traverse하는 능력이 떨어진다.
- 데이터가 산재된 확률이 높아 빈 버킷도 체크하면서 순회해야 하기 때문이다.
-
지역참조성에 취약하다.
- 해시 테이블의 조회 자체가 버킷들을 건너뛰면서 확인하는 방식이기 때문이다. 그렇기에 프로세스가 계속해서 캐시 미스를 발생시키고 이는 오버헤드로 이어진다. 데이터가 적고 type이 간단한(Integer…) 경우에는 배열을 이용한 자료구조가 더 나은 성능을 보일 수 있다.
장점
- 데이터 삽입, 삭제, 조회가 빠르다.
- 기본적으로 키 값으로 데이터를 찾으려면 해시 함수를 한 번만 실행하면 되기 때문이다.
해시테이블은 매우 빠르게 데이터를 삽입하거나 삭제하거나 조회할 수 있다고 했다.
하지만 충돌이 발생할 경우는 어떨까?
찬찬히 살펴보자!
해시 함수란?
임의의 길이를 갖는 데이터를 고정된 길이의 데이터로 매핑하는 함수이다.
매핑전 원래 데이터의 값을 키(key), 매핑 후 데이터의 값을 해시값(Hash Value) 또는 해시코드 라고 하며,
키(key)와 값(value)으로 매핑되는 과정 자체를 해싱(Hashing) 이라고 한다.
대표적인 해시 함수들
Division Method (나눗셈 법)
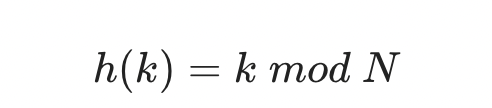
함수를 적용하고자 하는 값을 해시 테이블(N)의 크기로 나눈 나머지를 해시값으로 사용하는 방법이다.
해시 테이블의 크기를 알 때 사용할 수 있다.
테이블의 크기를 소수로 정하고 2의 제곱수와 먼 값을 사용해야 효과가 좋다고 알려져 있다.
N의 제곱꼴이 2^p일 때 k의 하위 p개의 비트를 고려하지 않기 때문이라고 한다.
Digit Folding (자리수 접기)
각 Key의 문자열을 ASCII 코드로 바꾸고 값을 합한 데이터를 테이블 내의 주소로 사용하는 방법이다.
Multiplication Method (곱셈 법)
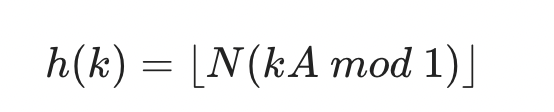
0<A<1인 A에 대해
kA mod 1 는 kA 의 소수점 이하 부분이다.
여기에 N을 곱하면 0~N사이의 값이 된다.
N이 어떤 값이라도 잘 동작하는 장점이 있고, A를 잘 잡는 것이 중요하다.
Univeral Hashing
다수의 해시함수를 만들어 집합 H에 넣어두고, 무작위로 해시함수를 선택해 해시값을 만드는 기법이다.
해시 충돌 (Hash Collision)
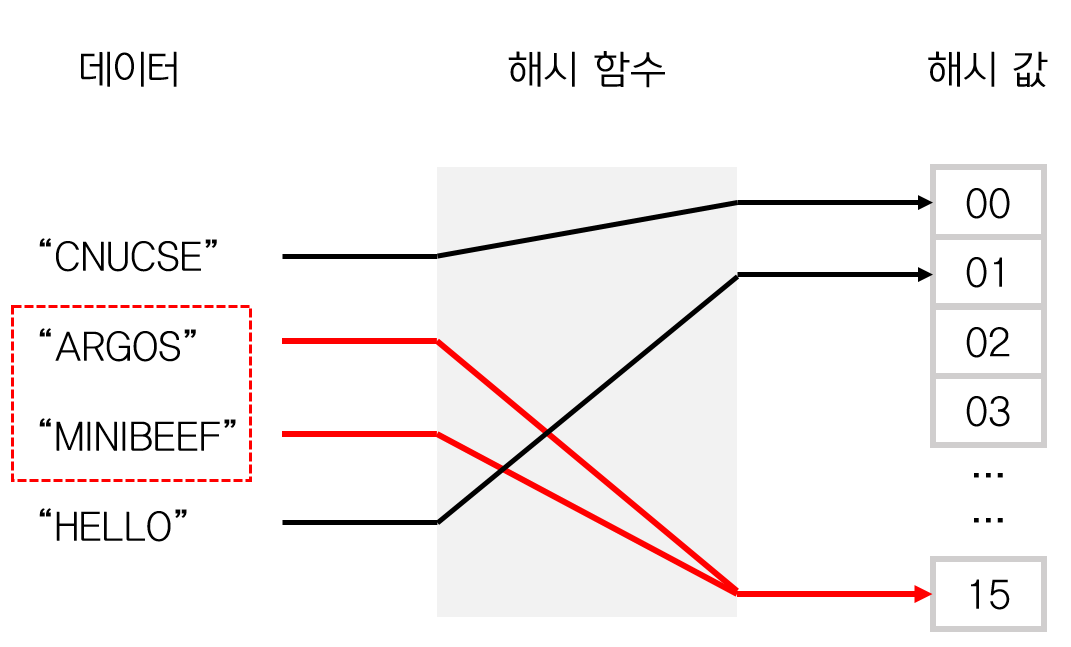
이렇게 다른 키 값에 해시 함수를 돌렸는데 같은 해시 값이 나오는 경우가 있을 수 있다.
이런 경우를 해시 충돌이라고 하고 이를 해결하는 방법은 크게 두 가지가 있다
해시 충돌 해결 - 분리 연결법 (Separate Chaining)

동일한 버킷에 저장되어야하는 데이터에 체인을 걸어 찾는 데이터가 나올 때까지 계속 체인을 따라가는 방식이다.
다른 자료구조를 버킷에 연결해서 다음 데이터를 저장한다.
장점
- 버킷을 계속 사용해야하는 개방 주소법에 비해 테이블의 확장을 늦출 수 있다.
- 확장은 O(m) , (m은 key의 개수)의 시간복잡도를 요하기 때문에 꽤 치명적이다.
단점
- 데이터의 수가 많아지면 동일한 버킷에 chaining되는 데이터가 많아지며 그에 따라 캐시의 효율성이 감소한다.
자료구조로 보통 링크드 리스트를 사용한다고 알고있는데, 트리를 사용하기도 한다.
1. 링크드 리스트 활용
각각의 버킷들을 연결리스트로 두어 충돌이 발생하면 해당 버킷의 리스트에 추가하는 방식이다.
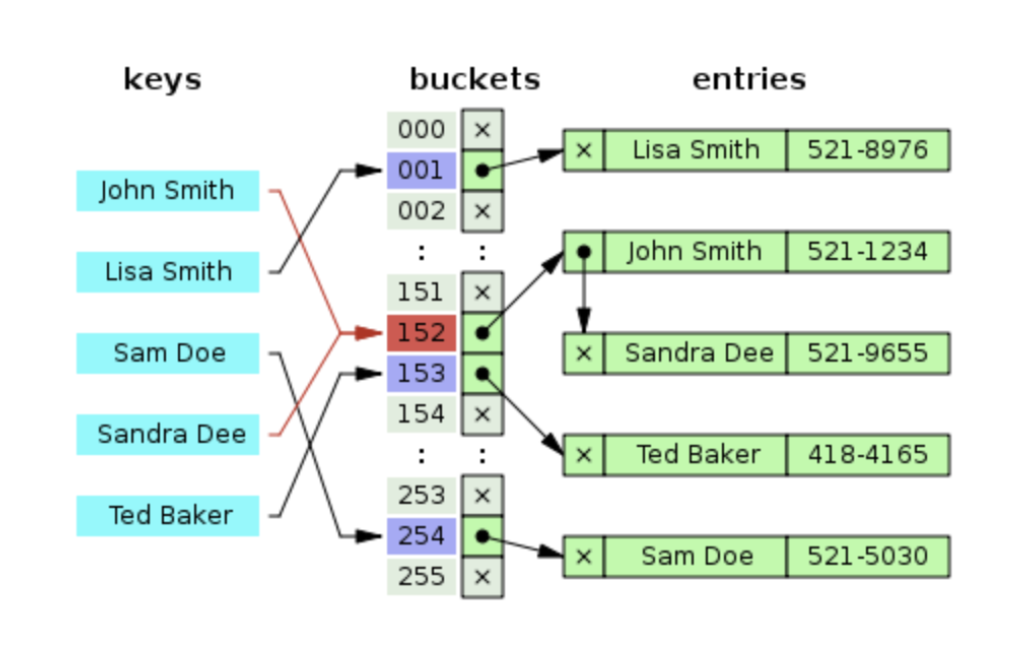
장점
- 간단하게 구현할 수 있다.
단점
-
개방 주소법에 미해 데이터 양이 적을 경우 연결 리스트 자체의 메모리 오버헤드가 있다.
- 연결리스트로 구현할 경우 다음 노드를 가리키는 포인터를 위한 공간이 필요해 메모리를 더 잡아 먹기 때문이다.
당연히 데이터가 적다면 충돌도 적게 발생할텐데 모든 버킷을 연결리스트로 만들면 그만큼 메모리 낭비가 있을 것이다.
- 연결리스트로 구현할 경우 다음 노드를 가리키는 포인터를 위한 공간이 필요해 메모리를 더 잡아 먹기 때문이다.
-
최악의 경우 탐색에 O(n)의 시간 복잡도가 걸린다.
- 버킷을 찾는 건 O(1)이지만 찾아야 하는 데이터가 연결리스트의 끝에 있을 경우,
연결리스트는 처음 노드부터 순차적으로 탐색하며 데이터를 찾아야 한다.
- 버킷을 찾는 건 O(1)이지만 찾아야 하는 데이터가 연결리스트의 끝에 있을 경우,
2. 트리 활용
연결리스트의 단점을 개선하기 위해 나온 것으로 연결리스트가 아닌 Tree 구조를 이용해 데이터를 저장한다.
단, 트리에서도 데이터가 편향돼 있으면 O(n)의 시간 복잡도를 가질 수 있다.
따라서 red-black Tree와 같은 균형이진 트리(Balanced Binary Tree)를 사용해 O(logn)의 연산을 보장한다.
하지만 적은 데이터 수에서 RB 트리를 유지하는데 드는 메모리 사용량이 연결리스트 보다 크기 때문에
어느 정도 데이터가 들어왔을 때 전환하는 것이 좋다.
Java 8에서 부터는 데이터가 8개가 넘으면 트리로 전환하고, 6개가 되면 다시 연결리스트로 전환한다.
두 개의 차이가 나는 이유는 1개 단위로 하면 전환하는 오버헤드가 더 크기 때문이다.
AVL트리가 아닌 RB트리를 사용하는 이유는 뭘까?
해시 테이블 같은 경우에 데이터 조회만 엄청 많이 일어나는 게 아니기 때문에,
rotation같이 밸런스를 유지하기 위해 드는 오버헤드가 너무 크다.
RB 트리는 조금 더 느슨하게 균형을 유지하면서 조회,삽입,삭제에 평균적으로 좋은 퍼포먼스를 보여준다.
이진 탐색 트리에 대해 정리했던 이전 포스팅을 참고해봐도 좋을 것 같다
장점
- 삽입,삭제,조회에 O(log(n))을 보장한다.
단점
- 메모리 사용량이 연결리스트 보다 크다.
해시 충돌 해결 - 개방 주소법(Open Addressing)
저장해야하는 인덱스에 값이 있으면 다른 인덱스에 저장하는 방법이다.
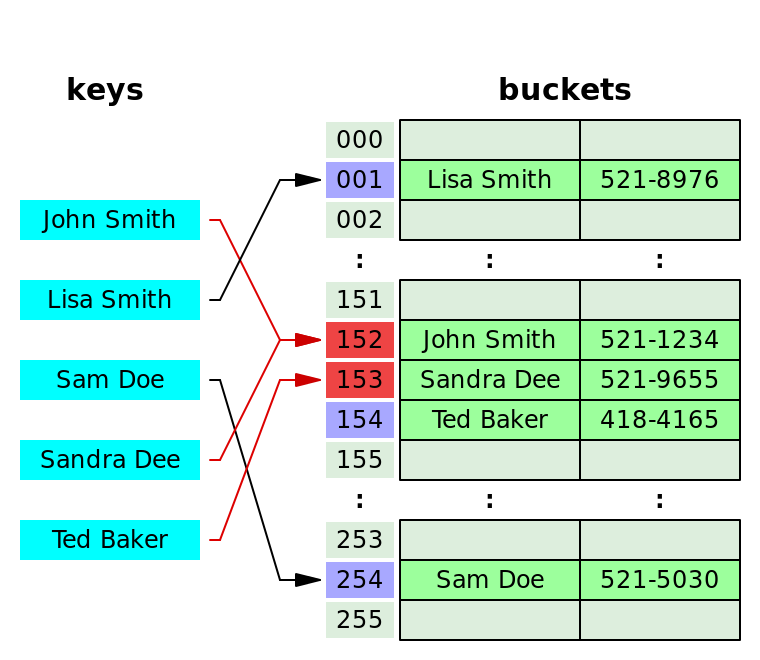
장점
- 적은 양의 데이터에 효과적이다.
- 메모리 효율이 분리 연결법에 비해 좋다.
- 메모리 할당에 대한 오버헤드가 없다.
- 분리연결법에 비해 캐시 효율이 좋다.
단점
- 테이블의 확장이 필요할 수 있다.
동작 방식
삽입
- 해시 값의 엔덱스가 차있으면 다음 인덱스로 이동하면서 빈 곳에 저장한다.
이렇게 비어있는 자리를 탐색하는 것을 탐사(Probing)라고 한다.
탐색
- 계산한 해시 값에 대한 인덱스부터 검사하며 탐사를 하는데 “삭제” 표시가 있는 부분은 지나간다.
삭제
- 탐색을 통해 해당 값을 찾고 삭제한 뒤 “삭제” 표시를 한다.
충돌 처리 방법 - 1. 선형 탐사(Linear Probing)

계산된 해시 값에서 충돌이 발생하면 고정폭만큼 건너 뛰면서 비어있는 인덱스에 저장하는 방법이다.
그 자리에도 차있으면 그 다음 고정폭만큼 건너 뛴다.
장점
- 단순해서 계산하기 쉽다.
- 캐시의 효율이 높다.
단점
-
최악의 경우 탐색을 시작한 위치까지 되돌아 온다. O(n)
-
특정 해시 값 버킷 근처에 값들이 뭉쳐서 평균 탐색 시간이 늘어난다. (primary clustering)
- x 라는 해쉬 값을 공유하는 객체들이 x+1,x+2,x+3 등으로 모이기 때문이다.
클러스터의 크기가 커질수록 비슷한 해쉬값들이 적절히 배치되지 못하고 다음을 probing하니 클러스터가 더 빠르게 자라난다. 다만 값들이 클러스터링 되어있기 때문에 cache hit 적인 측면에서는 유리하다. 처음 키에 대해서 접근을 하면 다음 키도 캐쉬에 올라와 있기 때문이다.
- x 라는 해쉬 값을 공유하는 객체들이 x+1,x+2,x+3 등으로 모이기 때문이다.
충돌 처리 방법 - 2. 제곱 탐사(Quadratic Probing)
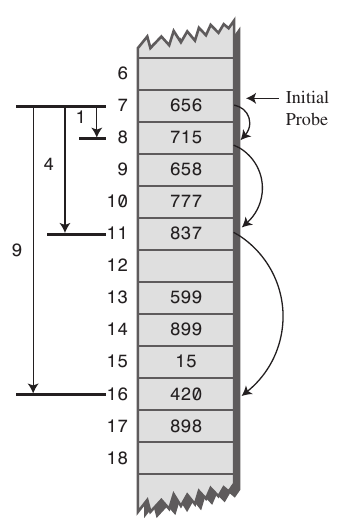
해시의 저장 순서 폭을 제곱으로 저장하는 방식이다.
예를 들어 처음 충돌이 발생하면 1만큼 건너뛰고, 다음 충돌이 발생하면 2^2, 3^2만큼... 으로 탐사를 한다.
장점
- 선형 탐사에 비해 폭넓게 탐사해 탐색, 삭제에 효율적이다,
단점
- primary clustering보다는 덜하지만 성능에 영향을 주는 secondary clustering 문제를 일으킨다.
- 만약 두 key의 처음 probe 값이 동일하다면 빈 slot을 찾는 과정이 동일하므로 같은 slot을 탐색한다.
즉 처음 충돌한 위치가 같다면 다음 충돌할 위치에서도 반복적으로 계속 충돌이 난다는 뜻이다.
- 만약 두 key의 처음 probe 값이 동일하다면 빈 slot을 찾는 과정이 동일하므로 같은 slot을 탐색한다.
충돌 처리 방법 - 3. 이중 해싱(Double hashing)
충돌이 생기면 2차 해시 함수로 다시 해싱을 해서 새로운 주소를 할당하는 방법이다,
장점
- 클러스터링에는 큰 영향을 받지 않는다.
단점
- 값이 퍼지게 되어서 캐시의 측면에서는 비효율적이다.
- 한번 더 해싱해서 새로운 주소를 할당하기 때문에 연산량이 많이 든다.
생각보다 공부해야할 내용이 많아서 오래걸렸다...
