Text Mining 07 Text Classification : Classification task, SSL

2KT·6일 전
Text Mining

1. 텍스트 분류(Text Classification)의 전체 흐름

핵심 관점 :

텍스트 -> 벡터로 표현 -> 분류기(Classifier)에 입력 -> 확률 계산 -> Loss 최소화 -> 성능 평가

2. 텍스트를 벡터로 표현하는 3가지 방식

1) Sparse representations

  • Bag-of-Words, TF-IDF
  • 고차원(|V|), 대부분 0
  • 단순하지만 의미 파악 어렵고 일반화 약함

2) Dense static embeddings

  • Word2Vec, GloVe
  • 단어당 하나의 벡터만 존재
  • 문맥 따라 의미 변하는 단어가 구분이 안됨

3) Dense contextual embeddings

  • BERT 등 Transformer 기반
  • 문맥마다 단어 벡터가 달라짐
  • Self-attention으로 문맥 정보를 학습

벡터 표현은 Sparse → Static Dense → Contextual Dense(BERT)로 발전

BERT는 MLM과 NSP로 사전학습하고, 분류기 head를 붙여 파인튜닝한다.

3. Pretraining -> Fine-tuning 패러다임

1) Pretraining

  • 웹의 대규모 텍스트를 이용해 비지도 또는 자가 지도 학습
  • "언어적 패턴"과 "세상 지식"을 대량 학습
  • Word2Vec / BERT의 MLM과 NSP가 해당
  • 목적 : 좋은 초기값(initialization) 획득

2) Fine-tuning

  • Downstream(실제목적) 작업에 맞게 BERT를 약간 수정
  • 전체 파라미터 업데이트(FULL) 또는 일부만 업데이트 (Partial)
  • 분류기 head를 붙이고 라벨 데이터를 이용해 supervised 학습
  • 목적 : task-specific knowledge 학습

장점 :

  • SGD는 초기값에 매우 민감함
  • Pretraining이 훌륭한 초기값을 제공 -> 적은 라벨로도 높은 성능 확보 가능

4. 분류(Classification)의 종류와 구조

1) Binary classification( |C| = 2 )

  • 스팸/비스팸, 긍정/부정 등
  • 출력확률 : sigmoid
    sigmoid+BCE

    2) Multi-class classification( |C| > 2 )
  • 클래스가 3개 이상
  • 출력 확률 : softmax
    softmax+CE

    3) Multi-label classification
  • 여러 라벨이 동시에 1 가능
  • 각 라벨마다 Sigmoid 독립 적용
  • Loss : 라벨별 BCE를 모두 더함
    sigmoid+BCE(독립)

5. 분류기의 구조

  1. 입력 텍스트 -> BERT 로 contextual embedding 생성
  2. 문장 representation 선택
  • [CLS] 벡터 또는 모든 단어 embedding의 평균
  1. Classification head 추가
  2. Logits 계산
  3. Sigmoid 또는 Softmax로 확률 계산
  4. Loss 최소화

6. Loss function

1) Binary Classification -> BCE Loss
Log-likelihood 최대화 <-> BCE 최소화

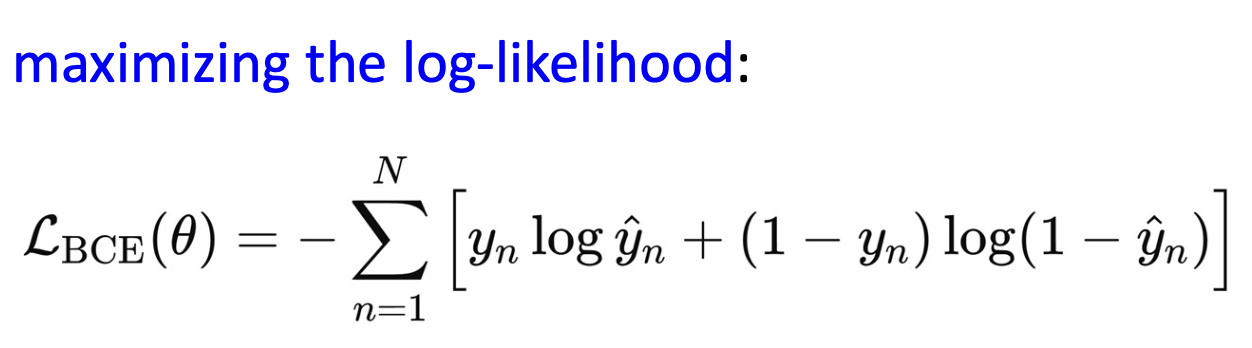
2) Multi-class Classification -> Cross Entropy(CE) softmax
여러 클래스 중 1개만 정답

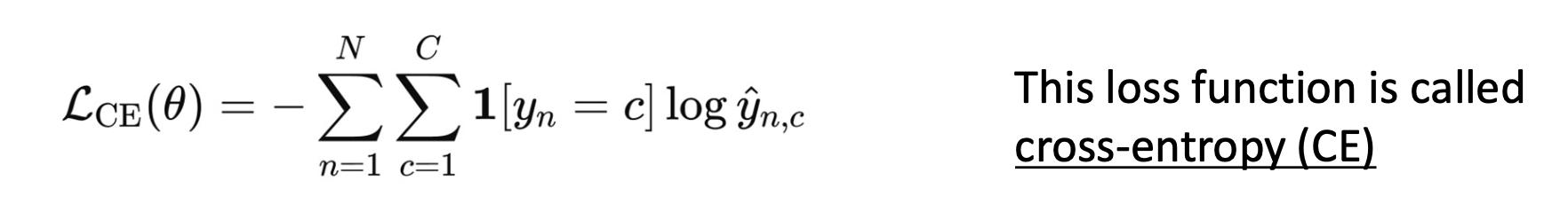
3) Multi-label Classification -> 클래스별 BCE 합 sigmoid

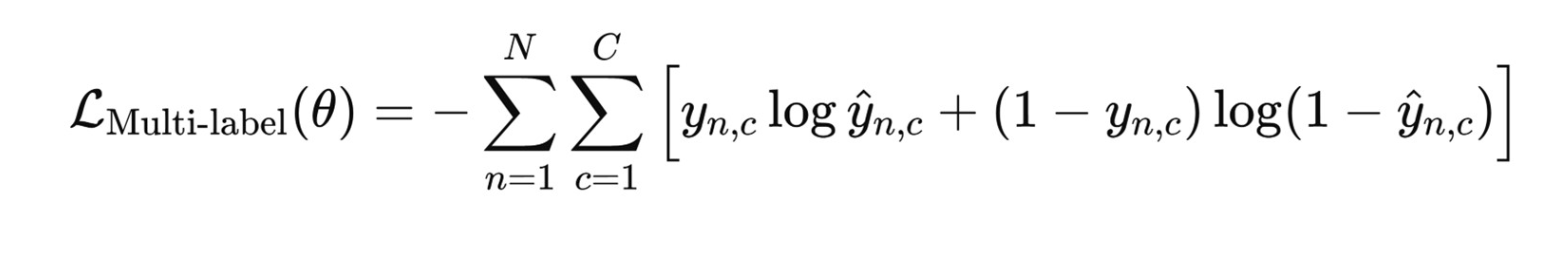
독립적인 Bernoulli variable로 모델링 되어 개별적으로 sigmoid 사용하는 것이 적합

요약

Sigmoid는 Bernoulli 가정, Softmax는 Categorical 가정
Binary(2 class) softmax = sigmoid(logit_1 - logit_2) -> 본질적으로 동일함
Binary일 때 softmax 대신 sigmoid를 사용할 수 있는 이유 : Binary softmax는 logit 차이에 대한 sigmoid의 동치이기 때문

7. 평가(Evaluation)

1) confusion matrix

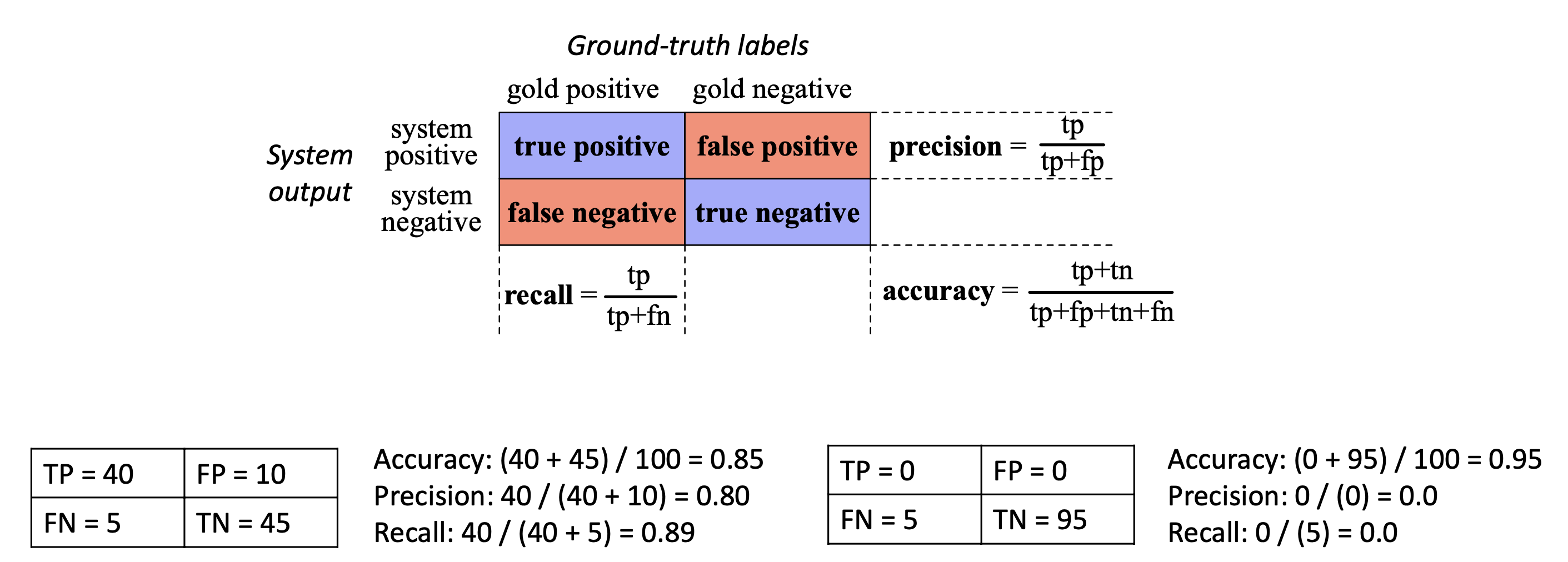
정확도에 의존하는 건 그렇게 좋지 않음
Precision, Recall은 trade-off 관계
F1 score : 2PR / P+R (P : precision , R : Recall) P,R 모두 높아야 F1 높아짐. P, R 중 하나라도 낮아지면 F1도 낮아짐

2) Multi-class 평가
Per-class metrics 계산 후

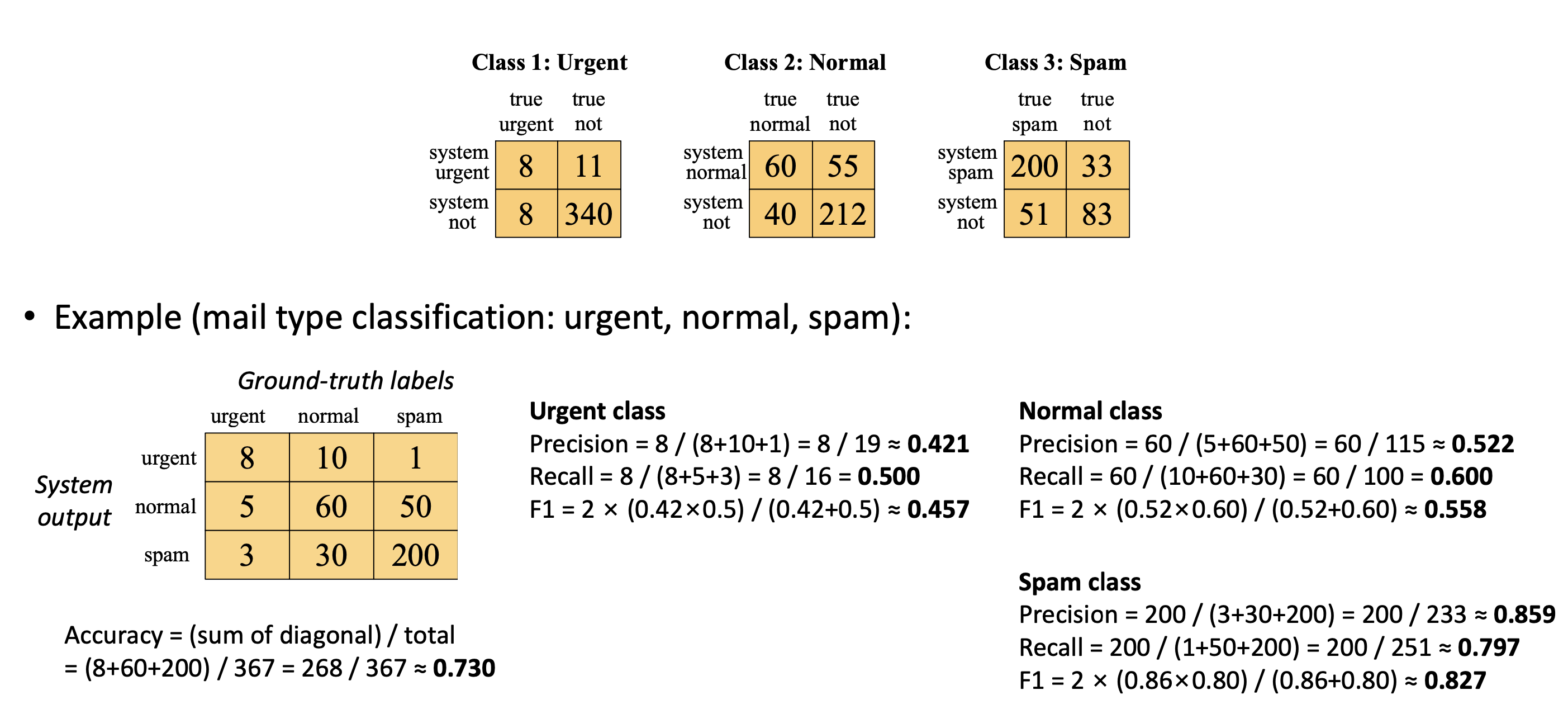
  • Macro-average : 클래스별 F1의 평균(클래스 균등 취급)
    위의 예시에서 구한 각각의 클래스별 행렬값에서 P/R/F1 score 구해서 3으로 나눠줌

  • Micro-average : 전체 TP/FP/FN을 합쳐 계산 (큰 클래스 영향 큼)
    위의 예시에서 구한 각각의 클래스별 행렬 3개를 하나의동일한 크기의 2x2 행렬로 합쳐서 (268, 99, 99, 635) 계산

Macro는 소수 클래스의 성능을 반영하기 때문에(클래스 균등 취급), 불균형 상황에서 중요하게 쓰일 수 있고, Micro는 전체적인 성능을 평가할 때 적합하다.

Semi-supervised learning (SSL)

이전내용까지는 : 라벨이 모두 존재한다 는 가정에서 BERT 등 pretrained model을 fine-tuning 하는 방식

How can we effectively leverage unlabeled data?

현실 : 대부분의 데이터는 라벨링이 되어있지 않고, 사람 라벨링은 비용이 비싸고 시간도 많이듬

-> 그래서 Semi-supervised learning이 필요

1. Semi-supervised Learning의 핵심 가정

1) Smoothness Assumption(부드러움 가정)

  • 입력 공간에서 가까운 데이터 포인트는 같은 라벨을 가진다.
  • "비슷하게 생긴 것은 비슷한 의미를 가진다"

2) Low-density Assumption(저밀도 가정)

  • 결정 경계는 데이터가 적게 분포된 영역을 지나야 한다.
  • 데이터가 많은 지역을 가로지르는 경계는 나쁜 결정경계
    -> 우리의 예측이 급격하게 바뀌어선 안된다.

-> SSL 기법들은 이런 가정에 기반해 boundary를 조정하는 방식으로 동작함

두 가지 대표적 접근법
1. Pseudo-labeling(자기-라벨링)
2. Consistency regularization(일관성 규제)
두 가지 접근법 서로 상호보완적이며 요즘 모델들은 두 가지 방법을 결합하여 사용함

Pseudo-labeling

개념 :

  • 모델이 unlabeled data에 대해 스스로 예측한 높은 confidence label을 pseudo-label로 사용
  • 마치 라벨이 있는 것처럼 학습에 포함시키는 방식
  1. 라벨링된 데이터로 먼저 supervised training
  2. 학습된 모델로 unlabeled data를 예측
  3. high-confiedence 샘플만 pseudo-label로 선택
  4. labeled + pseudo-labeled 데이터로 다시 학습(self-training = pseudo labeling을 반복 하는것)
    -> 반복하면 unlabeled 데이터에 대한 supervision이 점점 넓어짐

장점

  • 직접적인 학습 신호 제공
  • 라벨링을 자동화하여 라벨 부족 문제 완화

단점

  • Error propagation
    잘못된 pseudo-label이 학습 과정에서 강화됨
  • Overconfidence 문제
    모델이 틀릭 예측도 확신하게 되는 현상
    -> 모델의 초기 예측이 불완전하면 error propagation 발생

Consistency regularization

개념 :

  • 같은 입력에 작은변화(perturbation) 를 줘도 모델의 예측은 일관적이어야 한다.
    small noise를 벡터에 추가하거나, minor word change 등
  • 즉, 입력 x와 x̃(perturbed version)에 대해 출력 분포가 비슷해야 함

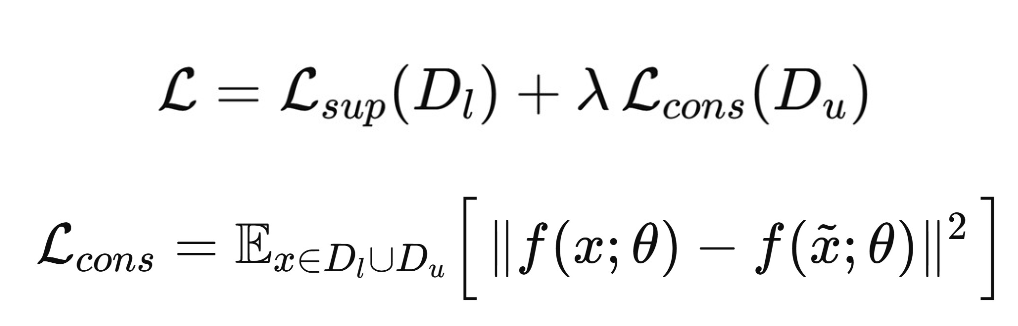
구현 예시

  • 임베딩에 noise 추가
  • dropout, masking
  • 데이터 augmentation(vision에서 crop/rotate)

핵심 효과
1. 결정 경계가 high-density를 피하게 됨
-> low-density assumption을 강하게 반영
2. regularization 효과
-> 모델의 confidence를 낮춰 overfitting 방지
3. unlabeled 데이터를 전부 활용 가능
-> pseudo-labeling은 high-confidence만 쓰는데, consistency는 모든 unlabeled data 사용

한계

  • 명시적인 라벨 신호가 없어서 boundary가 여전히 모호할 수 있음
  • perturbation(미세한변화) 품질에 따라 성능이 크게 좌우됨

Consistency Regularization의 고도화 : Temporal Ensemble

Pseudo labeling도 consistency도 둘 다 prediction instability 문제가 있다 -> 해결책이 ensemble

문제 : 예측이 epoch마다 흔들림

  • unlabeled data는 정답이 없어서
  • 매 epoch마다 softmax 출력이 흔들림 -> consistency loss 가 불안정해짐

해결 : Ensemble
1. model ensemble

  • 여러 모델의 출력을 평균하면 안정적
  • 하지만 비용이 매우 큼
  1. Temporal ensemble -> 모델은 하나, epoch별 예측을 합치기
  • 여러 모델을 쓰는 대신 이전 epoch들의 모델 출력을 누적해서 평균냄
  • Exponential Moving Average(EMA) 사용

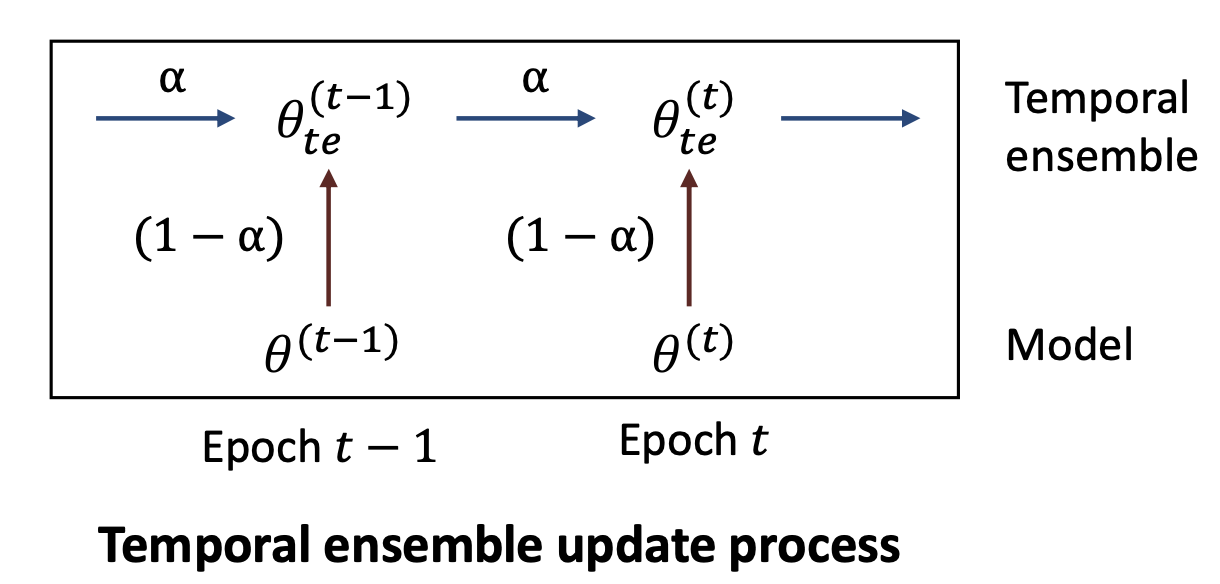
  • Prediction이 훨씬 안정적 -> unlabeled 데이터에 대한 pseudo target이 훨씬 reliable 해짐

EMA로 "안정성 확보", 매 epoch마다 model의 noisy prediction을 smoothing 해서 Stable prediction 가능

  1. Pseudo-labeling vs Consistency Regularization
방법장점단점
Pseudo-labeling강한 학습 신호 제공(직접적인 라벨)오류 전파, overconfidence
Consistency모든 unlabeled 데이터 활용, regularization 효과라벨 신호 약함

정리

  • labeled data가 부족한 실전환경에서 중요
  • SSL의 두가지 가정 : Smoothness, Low-density assumption
  • Pseudo-labeling: high-confidence 예측을 라벨처럼 사용. 장점: 직접 지도 / 단점: error propagation.
  • Consistency regularization: perturbation에도 출력이 동일해야 한다. 장점: 안정화·unlabeled 전체 활용 / 단점: 라벨 신호 약함.
  • Temporal ensemble(EMA): 예측 흔들림을 시간 평균으로 안정화해 consistency 학습 효과 극대화.
profile
2KT
2KT
이전 포스트

Text Mining 06 Dense contextual representation : BERT

다음 포스트

Text Mining 08 Text Classification : MTL(Multi-task learning)

0개의 댓글