자료구조 - 트리
트리의 특징
- 비선형 구조의 자료구조
- 노드 간의 계층이 존재 -부모노드(수퍼), 자식노드(서브)
- 그룹이 존재
트리의 용어
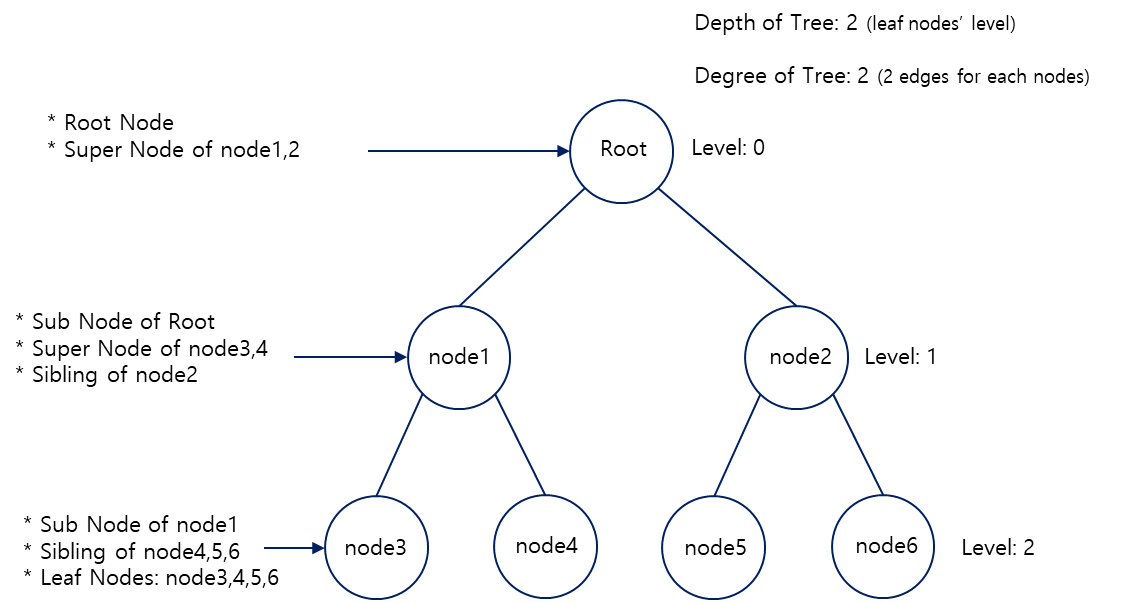
-
루트 노드(Root Node): 최초의 노드이자 트리 구조의 가장 위에 존재
-
부모 노드(Super Node): 수퍼노드라고도 하며, 해당 노드 아래(다음 계층)에 가지처럼 뻗어난 자식 노드가 있다.
-
자식 노드(Sub Node, Child): 부모노드로부터 다음계층으로 뻗어져 나오는 노드
-
형제 노드(Sibling Node): 부모 노드가 같지 않아도 되며, 계층이 같은 노드들을 의미
-
단말 노드(Leaf Node): 맨 마지막 계층에 있는 노드
-
내부 노드(Internal Node): 리프노드가 아닌 노드
-
차수(Degree): 트리의 노드가 가질 수 있는 최대 자식노드의 개수. 차수가 2이면 이진트리 3이면 3진트리
-
계층(Level): 루트노드에서부터 갖는 서브노드의 깊이. 루트노드는 0이며 루트노드의 자식노드는 1이 된다.
-
높이(Depth): 전체 트리를 이루는 계층의 깊이. 리프노드의 레벨로 파악하면 된다.
-
엣지(Edge): Link 또는 Branch라고도 하며 노드를 잇는 선을 뜻한다.
트리의 종류
이진트리(Binary Tree):
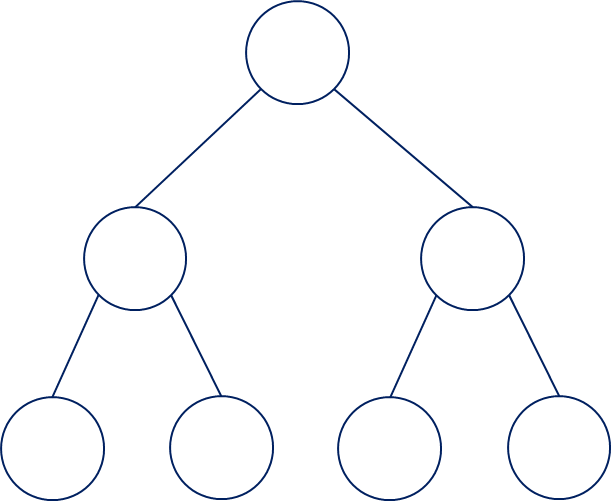
루트 노드를 중심으로 두 개의 서브트리로 나눠진다. 서브트리의 루트노드에서 또다시 두 개의 서브트리로 나눠지는 트리구조. 모든 트리구조의 핵심이자 다른 알고리즘과의 연결이 된다.
* 루트 노드에서 나눠지는 서브 트리 개수가 n개 이면, n진트리(ex 삼진트리, 사진트리)
이진트리의 구조 별 이름
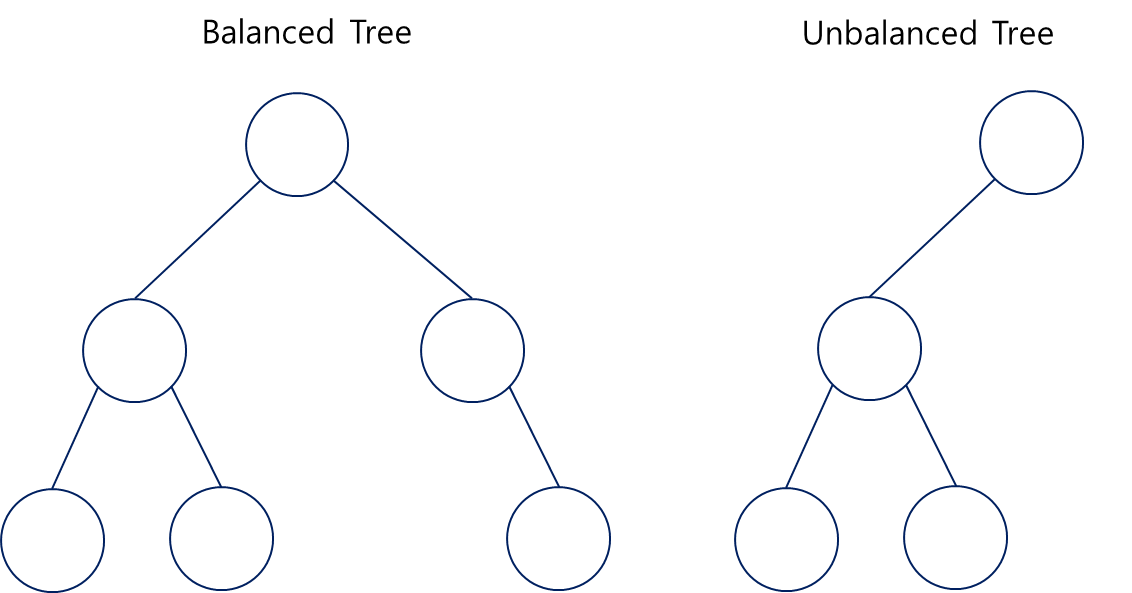
Blanced / Unblanced
대칭 비대칭을 기준으로 트리를 구분하는 방법 이미지와 같이 완전히 대칭일 필요는 없다.
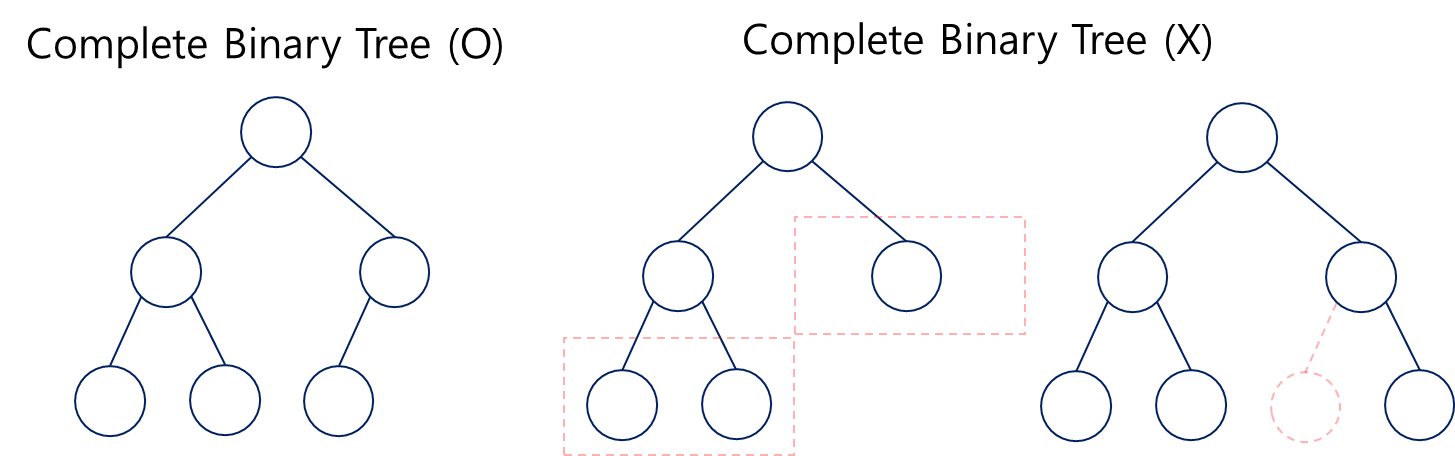
Complete Binary Tree
완전이진트리라고도 불린다. 노드가 왼쪽부터 채워졌고, 레벨이 같은 경우를 뜻한다.
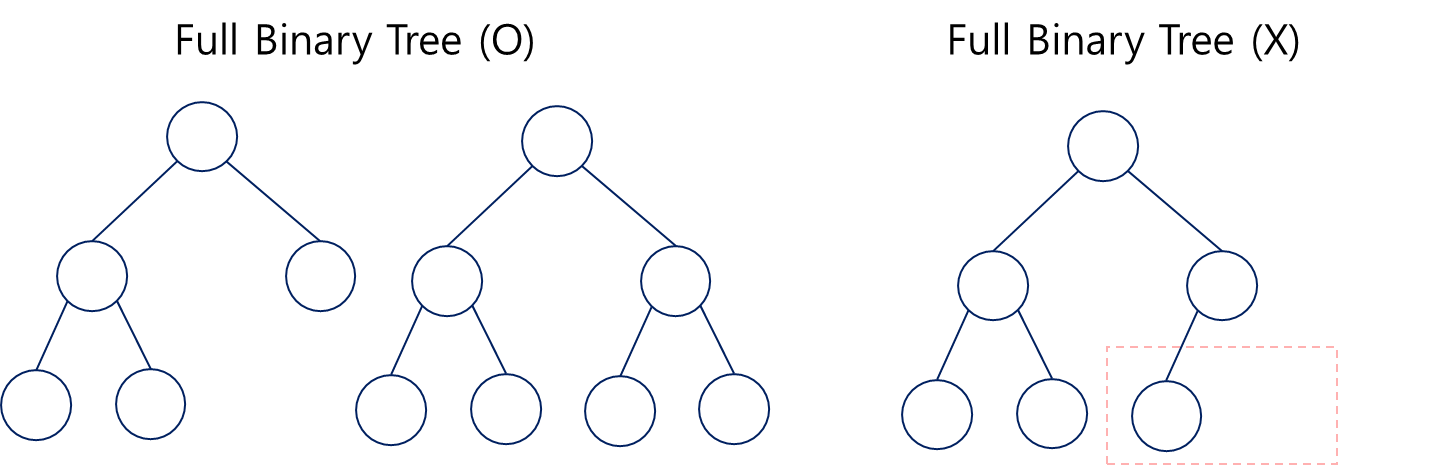
Full Binary Tree
각 노드들이 자식노드를 두 개씩 갖거나, 아예 갖지 않는 트리
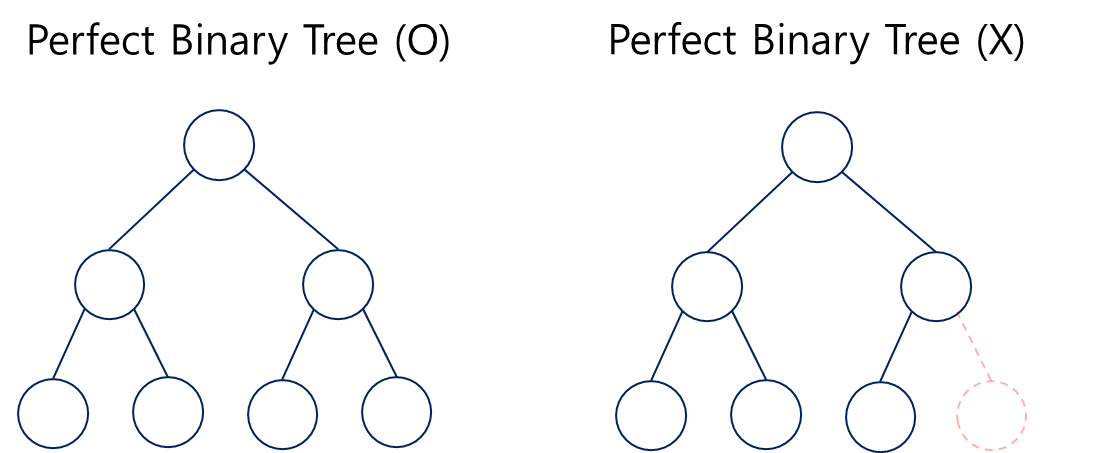
Perfect Ninary Tree
노드가 빈 공간이 없이 완전히 채워져 있는 상태의 트리.
이진검색트리(Binary Search Tree)
이진탐색을 수월하게 하기 위해 연결리스트와의 결합을 진행한 트리구조.
* 연결리스트는 삽입과 삭제가 시간복잡도 O(1)으로 빠른 강점을 갖고 있지만 탐색을 진행할 경우 head부터 탐색해나가기 때문에 최악의 경우 O(N)의 시간이 걸린다.
* 반면 이진탐색은 탐색의 시간이 O(logn)으로 매우빠른 장점을 갖고 있지만, 삽입과 삭제가 불가능하다.
이러한 특징을 갖고 있는 연결리스트와 이진탐색의 장점을 살려 탐색의 시간은 O(logn)이며, 삽입과 삭제가 가능한 자료구조로써 사용된다.
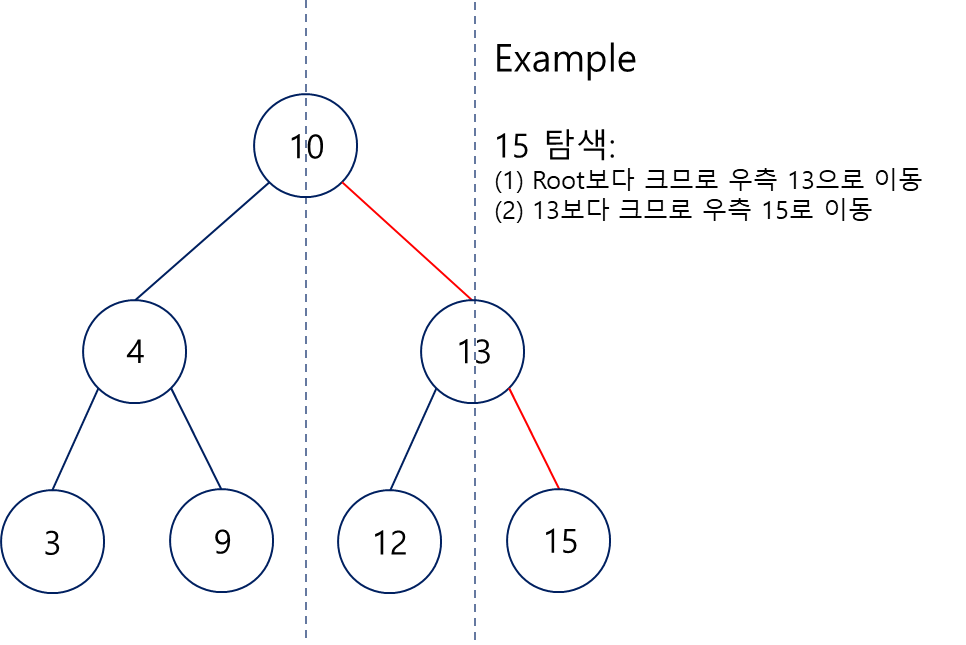
기능적 특징
- 반으로 쪼개 조건에 맞는 방향으로 찾아가기 때문에 빠른 탐색이 가능(시간복잡도 O(logn))
- 검색이 쉬워 노드 삽입역시도 쉽다
- 노드값을 검색순서에 따라 오름차순으로 얻는다 (조정 가능하다)
구조적 특징
- 연결리스트의 참조를 이용했기 때문에 좌측 -> 우측의 방향성을 갖고 있음
- 이진트리(Binary Tree)를 이용한 탐색방법으로 우측 노드는 좌측보다 커야하며 좌측 노드와 그 이하 자식노드는 그보다 작아야 한다.
(오른쪽 서브 노드 값 > 루트 노드값 > 왼쪽 서브 노드값) - Balanced Tree일수록 더 빨라진다.
- 규칙이 있어 구조가 단순하다
재귀함수를 이용한 이진탐색 구현
# 이분탐색 함수 작성
def Binary_Search(input_list, value_to_search, how_many_times):
how_many_times += 1 # 한번 재귀호출 될때마다 탐색 횟수를 카운트한다.
i = len(input_list)
if i == 1 and input_list[0] == value_to_search: # 배열이 최종적으로 1개 남았을때, 값이 맞으면
return f'{input_list}, {how_many_times}번 만에 탐색 성공!' # 결과와 횟수 리턴
elif i == 0: # 배열이 끝날때까지 없으면
return '아쉽게도 그 번호는 없소이다.' # 번호가 없음을 알린다.
mid = i // 2 # 배열의 중간값 찾기
if input_list[mid] == value_to_search: # 중간값 자체가 탐색값과 일치할 경우
return f'{input_list[mid]}, {how_many_times}번 만에 탐색 성공!'
elif input_list[mid] > value_to_search: # 중간값보다 값이 작은 경우
return Binary_Search(input_list[:mid], value_to_search, how_many_times)
elif input_list[mid] < value_to_search: # 중간값보다 값이 큰 경우
return Binary_Search(input_list[mid:], value_to_search, how_many_times)위와 같이 이분탐색 함수를 작성해봤다. 재귀함수를 이용해 중간값을 찾고, 탐색할 값이 그보다 높거나 낮으면 리스트를 반으로 줄여 나가므로 탐색의 속도가 으로 빠른편이다.
* 단, 이분탐색을 위해선 리스트(배열)이 정렬되어 있어야 한다.
# 임의의 정수 작성 - 정렬이 필요함
import numpy as np
# 0~1000 사이 중 랜덤 숫자 100개를 뽑고, 중복을 제거한 뒤, 오름차순 정렬
lst = sorted(set(np.random.randint(0, 1000, size= 100)))
print(lst[:10]) # 맨 앞의 10개
print(lst[-10:]) # 맨 뒤의 10개[output]
[0, 8, 15, 27, 72, 80, 83, 85, 98, 99]
[892, 901, 925, 933, 938, 965, 974, 976, 984, 991]times = 0 # 횟수 초기화
Binary_Search(lst, 991, times) # 7 맨 뒤 숫자
---
times = 0 # 횟수 초기화
Binary_Search(lst, 0, times) # 7 맨 앞 숫자[output]
991, 7번 만에 탐색 성공!
---
[0], 7번 만에 탐색 성공!맨 처음과 마지막 숫자를 찾는데에 7번 만에 찾는 것을 볼 수 있다.
그럼 연결리스트에서의 탐색은 어떻게 되는지 구현해서 알아본다.
연결리스트를 이용한 탐색 구현
class Node:
def __init__(self, value):
self.value = value
self.next = None
class Linkedlist:
def __init__(self, value):
self.head = Node(value)
def add_node(self, value):
node = self.head
while node.next:
node = node.next
node.next = Node(value)
def search_node(self, value):
how_many_times = 0
node = self.head
while node:
how_many_times += 1
if node.value == value:
return f"{value}, {how_many_times}번 만에 탐색 성공!"
elif node.value == None:
return f"{value}는 연결리스트에 없다."
else:
node = node.next 편의상 연결리스트의 삽입(add_node)과 탐색(search_node) 기능만 구현해봤다.
add를 통해 연결리스트를 만들고, search로 찾아보도록 한다.
# 클래스 선언과 함께 헤드를 만든다
hd = Linkedlist(lst[0])
# 헤드를 제외한 나머지를 add한다.
for i in lst[1:]:
hd.add_node(i)
# 연결리스트의 맨 뒤 숫자
hd.search_node(lst[-1])
---
# 연결리스트의 맨 앞 숫자
hd.search_node(lst[0])[output]
991, 96번 만에 탐색 성공!
---
0, 1번 만에 탐색 성공!연결리스트로 아까와 같은 리스트의 값을 탐색했을때, 맨처음의 값을 바로 찾으면 빠르게 찾게되지만, head부터 찾아가기 때문에 맨마지막 숫자를 탐색 대상으로 두면 모든 값을 거쳐가야한다.
그렇기에 이진탐색의 장점을 연결리스트에 접목해 트리구조로 만든 것이 이진탐색트리이다
이진탐색트리를 이용한 탐색 구현
class Node_Tree:
def __init__(self, value):
self.value = value
self.right = None
self.left = None
class Binary_Search_Tree:
def __init__(self, value):
self.root = Node_Tree(value)
def add_node(self, value):
self.node = self.root
while self.node != None:
if self.node.value < value:
if self.node.right ==None:
self.node.right = Node_Tree(value)
break
else:
self.node = self.node.right
elif self.node.value > value:
if self.node.left == None:
self.node.left = Node_Tree(value)
break
else:
self.node = self.node.left
def search_node(self, value):
node = self.root
how_many_times = 0
while node:
if node.value < value:
node = node.right
how_many_times += 1
elif node.value > value:
node = node.left
how_many_times += 1
elif node.value == value:
return f"{value}, {how_many_times}번 만에 탐색 성공!"
if self.node == None:
return f"{value}는 트리에 없다."Node_Tree함수에 right와 left의 속성을 추가하여 양쪽으로 노드를 추가할 수 있는 구조를 이용했다. 기본적인 원리는 이분탐색과 같은데, 리스트 내에서의 로직이 아니라 연결리스트 구조를 변형해 만든 것.
BST 구현 시 알아둘 점
-
루트노드의 값은 가능한 전체 정보의 중간값이 될 수 있도록 한다.
이진탐색트리의 성능은 Balanced Tree일때 가장 좋다. 만약 0~10의 숫자 중 0을 루트노드로 둔다면, 왼쪽으로 서브노드를 형성할 0보다 낮은 값이 없기에 루트노드부터 서브노드를 한개만 가지게 된다. 이진탐색트리의 장점을 전혀 살리지 못할 수 있다. -
리스트를 반복문으로 넣어주려면 정렬하지 말고 섞어주어야 한다.
정렬된 리스트를 그대로 넣게되면 단순히 값이 낮으면 left, 높으면 right로만 향하기 때문에 루트노드를 제외하고는 모두 서브노드가 1개씩밖에 달리지 않게된다.
import copy
# 이진탐색트리 클래스 생성 -> root노드를 가능한 중간으로 해야 balanced tree가 구현된다.
n = len(lst)//2 # 가장 중간의 수를 고른다.
tr = Binary_Search_Tree(lst[n]) # 트리를 선언하고, 리스트의 중간 수를 root노드로 삼는다.
lst_tree = copy.deepcopy(lst) # 기존 배열의 보존을 위해 tree용 리스트를 만들고
lst_tree.pop(n) # root노드에 넣었던 녀석은 제거!
random.shuffle(lst_tree) # 랜덤하게 섞어준다. -> 섞지않으면 정렬되어있어 선형적인 리스트와 다를게 없다.
for i in lst_tree[1:]: # tree용 리스트의 내용을 tree에 본격 넣어본다.
tr.add_node(i)
tr.root.value # root노드를 확인해본다[output]
511# 리스트의 맨 뒤 숫자
tr.search_node(lst[-1])
---
# 리스트의 맨 앞 숫자
tr.search_node(lst[0])[output]
991, 6번 만에 탐색 성공!
---
0, 5번 만에 탐색 성공!위와 같이 이진탐색트리를 이용해 본 결과, shuffle을 이용했기에 기존 리스트 상에서의 인덱스가 어떻게 이뤄졌는지는 알 수 없지만, 맨마지막 숫자도 연결리스트 보다는 확연히 빠르게 탐색할 수 있는 것을 알 수 있다.