정렬 알고리즘 (Sorting Algorithm)

배열(array) 안에 있는 데이터를 일정한 규칙에 따라 오름차순 또는 내림차순으로 정리하는것을 의미. 알파벳 또는 숫자 등의 데이터들을 정리할 수 있다.
정렬을 함으로써 탐색을 효과적으로 할 수 있고(이진탐색 등에서 정렬이 필요), 겹치는 데이터를 찾기 위해서도 정렬이 필요하다.

정렬 알고리즘의 종류는 무수히 많지만, 그 중 입문시에 배우는 기본적인 세 가지 반복 정렬(Iterative sorting) 알고리즘에 대한 정리를 한다.

선택정렬(Selection Sort)

오름차순으로 정렬시, 배열 전체를 비교해 가장 작은 값을 찾아 차곡차곡 정리하는 방법.

정렬 방식

---

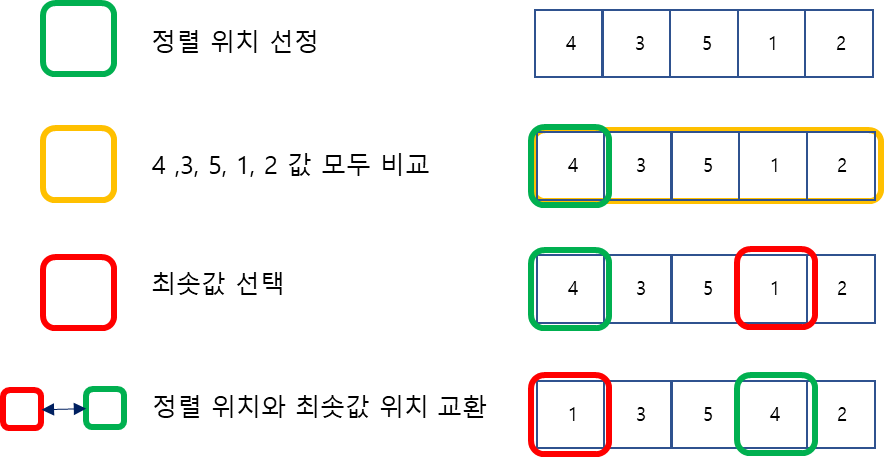
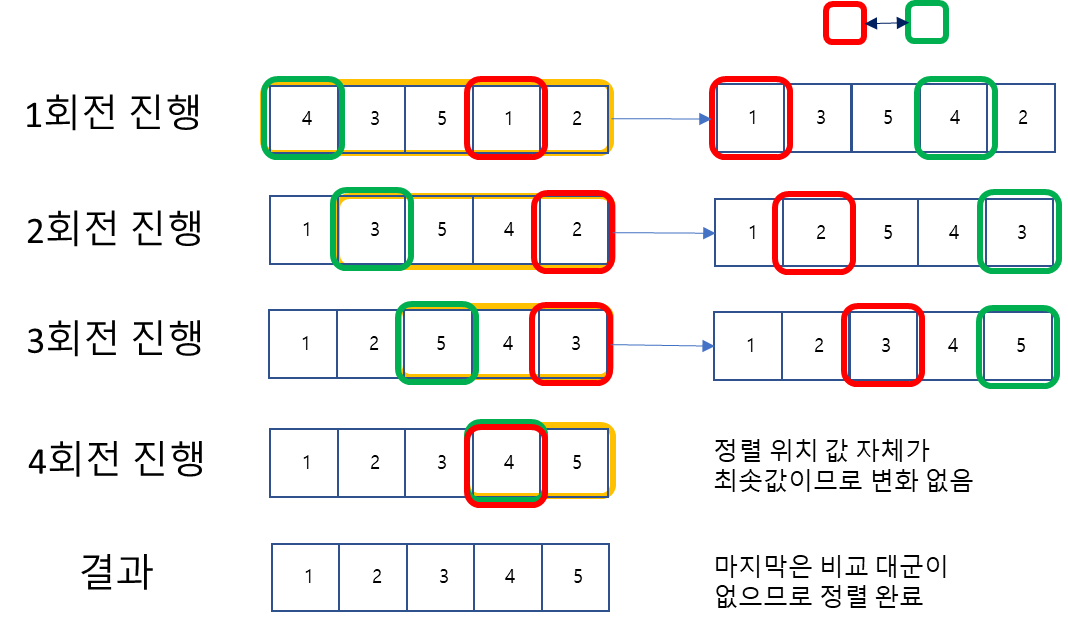
• 정렬을 진행할 위치를 정한다.
• 정렬 위치부터 이후의 값들을 모두 비교해서 최솟값을 찾는다.
• 최솟값을 정렬 위치의 값과 맞교환 한다.
• 정렬위치를 다음으로 이동시킨다.
• 상위 내용을 반복한다.

선택 정렬 구현

# 선택정렬 함수작성
def selection_sort(lst):
  for i in range(len(lst)):   # 리스트에서 왼쪽부터 순차적으로 정렬 위치 선택 
    for j in range(i+1, len(lst)): # 정렬 위치값과 비교할 값을 순차적으로 선정
      if lst[i] > lst[j]:        # 현재 정렬값 보다 낮은 값이 나오면
        lst[i], lst[j] = lst[j], lst[i]   # 해당 값과 바꿔준다.

lst = [2,6,4,3,10,1,7,5] # 리스트 생성
selection_sort(lst) #함수 적용
print(lst)  # 적용된 리스트 확인

[output]
[1, 2, 3, 4, 5, 6, 7, 10]

• 모든 값을 비교하고 정렬하기 때문에 시간복잡도가 $O(n^2)$으로 실행 시간이 긴 편이다.
• 안정성이 떨어진다. -> 같은 값을 가진 데이터가 있는 경우, 해당 값들의 순서가 바뀌면 안되는 경우에도 바뀔 수 있다.

* 앞쪽의 정렬 위치가 선정되면 그 이전 부분은 이미 정렬이 된 상태이기 때문에 비교를 안해도 되므로 코드 상에서도 이 부분을 고려해서 작성한다.

버블정렬(Bubble Sort)

인접한 두 데이터를 비교하여 큰 숫자를(오름차순시) 오른쪽으로 옮기는 것을 반복한다. 이 역시도 모든 데이터에 거쳐 비교를 해야하기 때문에 시간복잡도 $O(n^2)$인 정렬 방법이다.

---

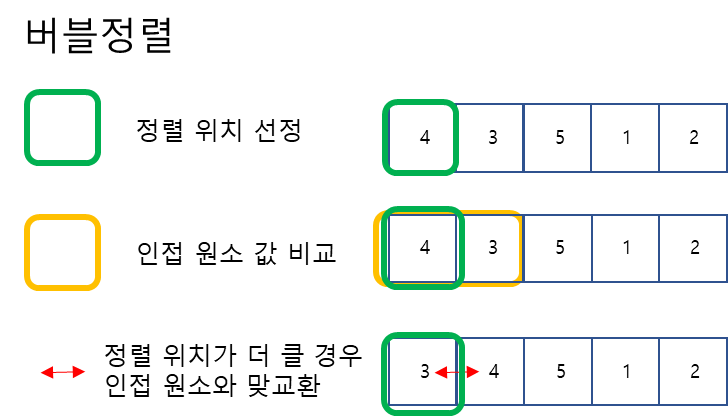
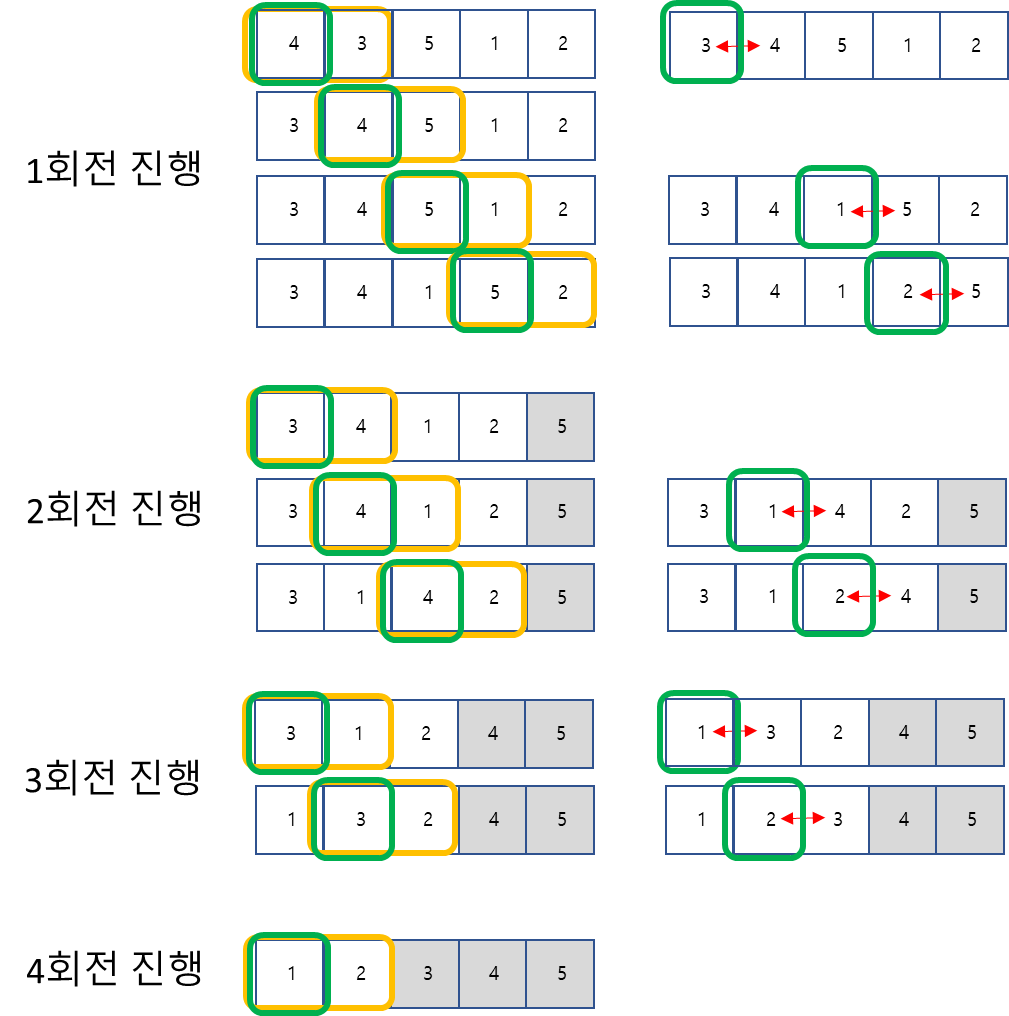
• 맨첫 인덱스부터 정렬 위치로 선정
• 인접한 오른쪽 원소와의 값 비교 진행
• 정렬 위치의 값이 더 큰 경우 둘의 위치를 바꿔주고, 아닐 경우 그대로 둔다.
• n-1번의 반복을 진행한다. (하나만 남으면 정렬할 필요 없으므로 n-1)

버블 정렬 구현

def bubble_sort(lst):
  for i in range(len(lst)): # 정렬 위치의 위치 정보를 i에 담는다
    block = len(lst)-i         # 반복을 진행할 때마다 맨 마지막 원소는 최대값으로 고정되므로 block으로 지정
    for j in range(block):     # block인 부분은 비교할 필요없으므로 그 이전까지만 반복
        if j +1 != len(lst):   # 인덱스 Out of Range Error 방지용 조건
            if lst[j] > lst[j+1]: # 정렬위치와 그 다음 인덱스의 값을 비교한다. 정렬위치의 값이 클 경우 
                lst[j],lst[j+1]  = lst[j+1],lst[j]  # 두 값의 위치를 바꿔준다.
lst = [2,6,4,3,10,1,7,5]
bubble_sort(lst)
print(lst)

[output]
[1, 2, 3, 4, 5, 6, 7, 10]

• 모든 값을 비교해야하므로 정렬 진행의 시간복잡도는 $O(n^2)$이다.
• 정렬이 되어있어도 비교를 해야 하므로 비효율적이다.
• 이웃만을 비교하므로 정렬진행이 안정적이다.

삽입정렬(Insertion Sort)

정렬된 원소들에 다음 원소의 위치를 파악해 삽입해나가는 정렬방법. 세 정렬 방법 중 그나마 Best일때엔 시간복잡도 $O(n)$의 결과를 가져올 수 있는 정렬방법이다.

---

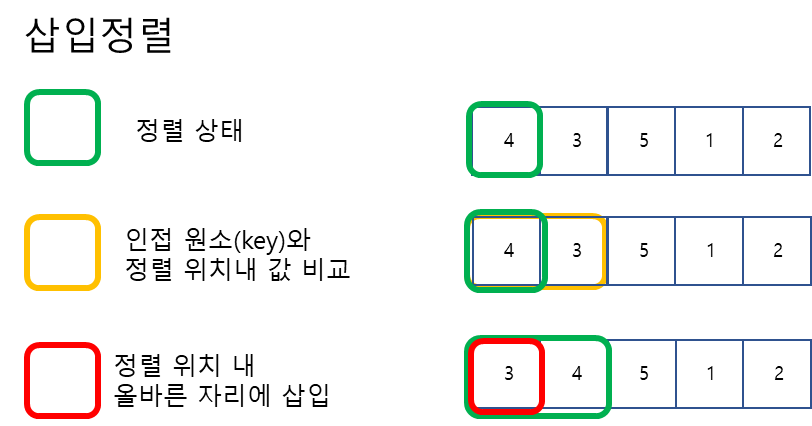
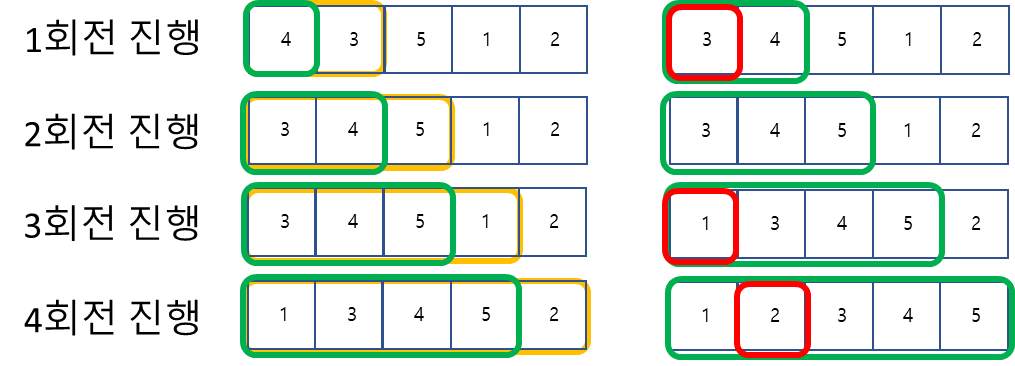
• 오름차순시 왼쪽부터 정렬해 나가면서 다음 원소(Key)를 그에 맞는 위치에 삽입하는 방식
• 정렬된 배열 내에 인접한 key값이 들어갈 위치를 찾아 삽입한다.

삽입 정렬 구현

def insertion_sort(lst):
  a = len(lst)          
  for i in range(a):    # 자료 수만큼 반복진행
    key = lst[i]        # 인접한 원소 = key
    j = i-1             # 인접한 원소보다 하나 앞서있는 원소 = 정렬구간의 원소
    while j >= 0 and lst[j] > key:  # 정렬구간내 원소가 Key값보다 클 경우
      lst[j+1] = lst[j]             # 해당 원소를 하나씩 밀어낸다.
      j -= 1                        # 그 다음 이전 원소를 파악한다.
    lst[j+1] = key                  # 위를 반복하다 while문이 끝나면(key보다 작은 값 발견시)
                                    # 해당 위치보다 뒷쪽에 key값을 삽입한다.
lst = [2,6,4,3,10,1,7,5]
insertion_sort(lst)

print(lst)

[output]
[1, 2, 3, 4, 5, 6, 7, 10]

• 데이터 수가 적을 때 이동 수가 많지 않아 효과적, 반면 너무 많아지면 적합하지 않음
• 버블정렬과 달리, 정렬이 되어있으면 그만큼 빠르게 진행가능
• 위와 같은 이유로 시간복잡도는 Best: $O(n)$, Worst: $O(n^2)$이다.