자료구조와 알고리즘에 대한 이론 공부를 정리해본다.
자료구조(Data Structure)
자료구조의 정의: 컴퓨터 과학 전체적인 관점의 기초공사 개념
(이게 무슨소리냐..)컴퓨터 기능을 효율적으로 동작하도록 하기 위한 어떠한 구조들이라고 볼 수 있다.
예를 들면 업무 자동화, 빠른 계산(계산기), 반복 처리, 여러 값에 대한 일괄처리 등 효율적으로 처리할 수 있도록 구조를 짜는 것.
자료구조와 효율성
자료구조를 활용하는 것은 효율을 높이기 위함. 실제 사용하는 서비스들이 조금이라도 실행이 지체되거나 느려지면 불편을 느끼듯 속도면에서의 효율이 중요하며, 메모리를 비효율적으로 사용하는 것도 바람직하지 않다. 이러한 점들을 파악한 것이 시간복잡도 및 공간복잡도이다.
- 시간복잡도: 실행 시간이 얼마나 긴지를 파악. S/W의 성능으로 볼 수 있다.
- 공간복잡도: 문제 해결에 필요한 메모리 저장공간이 어느정도나 되는지를 파악. H/W의 성능.
Big(O)표기법
N개의 데이터에 대해 연산을 얼마나 반복 또는 조작했는지에 따라 달라지는 시간복잡도의 표기방법이다. 모든 건들에 대해 정확한 시간을 책정할 수 없으므로 반복의 방식과 여부에 따라서 아래와 같이 계층을 나누어 확인한다.
- 상수시간: 단순 연산으로 한번 진행을 의미
- 로그시간: 연산을 반복하는데 특정 요인으로 인해 연산의 수가 줄어듦
- 선형시간: 전체 데이터 N에 대한 연산을 한번씩 진행해 선형으로 나타남
- 선형로그시간: 경우에 따라 전체 데이터 연산을 모두 수행해야 하는 경우도 있다. 연산의 수가 이다.
- 제곱시간: 전체 데이터 N에 대한 연산을 제곱으로 한다.
- 지수시간: 문제 해결을 위한 연산이 지수로 늘어난다. 상수값의 n제곱 만큼의 연산 필요.
위와 같이 시간복잡도(Time complexity)를 구분할 수 있으며, 각 알고리즘의 성능을 개략적으로 평가할때 이를 바탕으로 하게된다.
위 Big(O)표기는 시간이 적게 걸릴수록 성능이 좋다고 할 수 있으며, 불필요한 연산을 최소화 하여 성능을 최고로 끌어올리는 것이 목표이다.
ADT 자료구조 - 추상 자료형
기본적인 문자열(STRING) 정수 및 실수(INT, FLOAT) 등의 자료형은 넘어가고 ADT 관련 자료구조를 파악해보도록 한다.
Abstract Data Type으로 추상 자료형이라 불리는 자료구조들이 있다.
이는 추상적인, 개념적인 이론으로 그 구조를 이해하고 있어야 그와같은 아키텍처를 제작해 활용할 수 있는 자료구조이다.
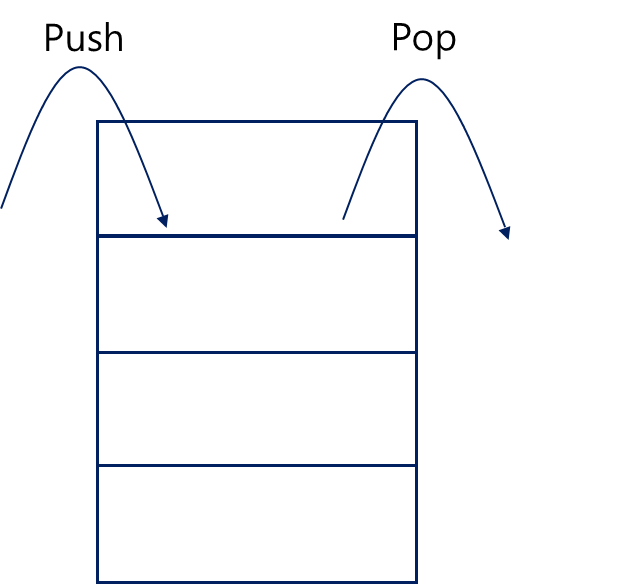
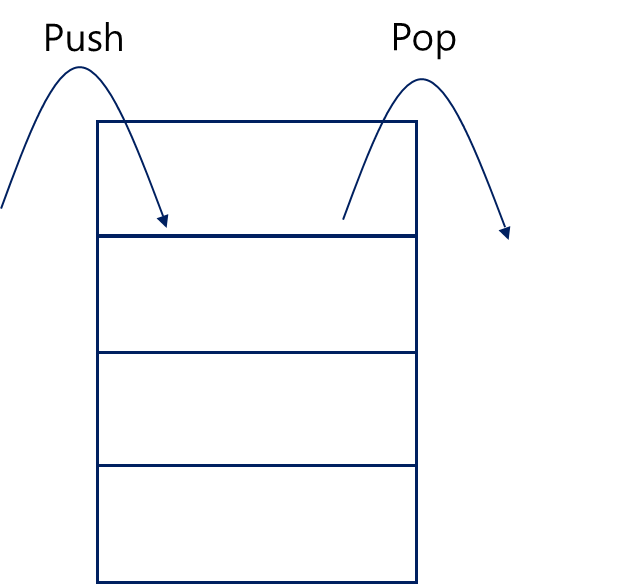
1. STACK 스택 - LIFO(Last In First Out)
스택은 후입선출이라 하여 마지막에 들어간 것이 가장 먼저 나오는 자료구조를 뜻한다.
어떤 물건을 쌓아둔 뒤, 꺼낼때는 맨 위(마지막으로 쌓아올린)의 것을 먼저 꺼내는 것과 같은 원리다.
일상에서도 많이 볼 수 있는데, 택배 상자가 트럭에 실릴때는 가장 나중에 내릴 것을 먼저 싣고, 금방 내릴 것은 최후방에 싣는 것을 예를 들 수 있다.
특징
- 한곳에서만 데이터를 넣고 뺄 수 있다는 점.
- 데이터의 입력을 Push, 출력을 Pop이라 한다.
- 활용 - 실행취소 / 페이지 뒤로가기 등
스택 오버플로우:
위 설명된 스택이 할당할 수 있는 메모리 이상으로 넘치는 현상을 말하며, 재귀함수가 무한히 지속되거나 한 함수에서 너무 큰 지역변수를 선언하면 발생할 수 있다고 한다. 개발자들의 정보공유로 유명한 플랫폼의 이름도 이와 같다.
오버헤드:
공부하는 김에 비슷한 이름도 같이 알아두자 일을 처리하는데 간접적으로 드는 시간을 의미하며 없을 순 없지만 최소화하면 좋은 녀석이다.
예를 들어, 물을 마시려는데 컵을 씻어서 물을 받아 마셔야 한다면, 문제 해결은 물만 마시면 되는것이지만, 이를 위해 우리가 취하는 행동(컵을 씻기)을 취하는 시간이 오버헤드이다.
컵을 10초 동안 씻고 물을 3초간 받아서 약 2초간 마셨다. 그럼 총 15초를 사용한 것이고 물을 마신 2초를 제외한 13초는 오버헤드이다. 이 오버헤드를 줄일 방법은 무엇이 있을까? 바로 컵을 씻어 놓는 것이다. 그렇다면 10초를 줄여 필연적으로 물을 받아야하는 3초의 오버헤드 외엔 많이 줄일 수 있게 된 것이다.
2-1. QUEUE 큐 - FIFO(First In First Out)
선입선출로 먼저 들어간 것이 가장 먼저 나오는 자료구조. 기본적인 대기열을 생각하면 된다. 흔히 음식점에서 줄을 서는 경우도 먼저 줄 서있던 사람이 먼저 입장하는 것과 같은 원리이다.
일부 대전게임을 할 때에도 준비한 뒤 게임을 시작하고자 할 때, '큐를 돌리다'라고 표현하는데 이때의 '큐'가 바로 자료구조에서의 Queue를 의미한다. 말 그대로 대기열을 생각하면 된다.

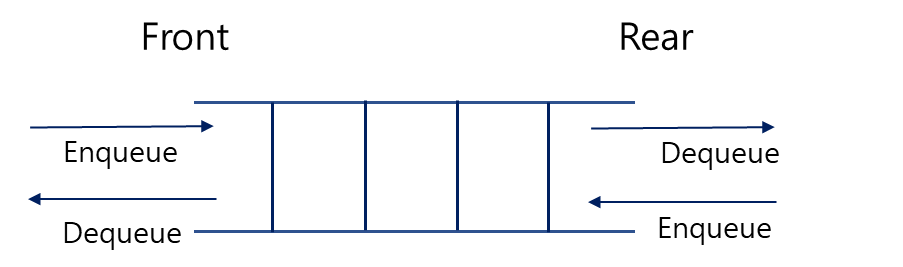
- 입력과 출력의 위치가 다르다.
- Front와 Rear라고 하며, 각각 입력은 Enqueue(인큐), 출력은 Dequeue(디큐)라고 한다.
- 데이터에 대한 접근은 Front 맨 처음 또는 Rear 맨 끝의 데이터로만 접근할 수 있다.
- 활용 - 콜센터 전화연결, 프린터(인쇄입력 우선순)
2-2 DEQUE 덱 - 양방향 큐
collection 패키지에 아예 deque라는 모듈이 존재하기까지 하는 덱은 큐와 스택을 합쳐놓았다고 할 수도 있고, 양방향 큐라고도 할 수 있다. 큐의 구조를 기준으로 front와 rear에서 모두 입력과 출력이 가능하기 때문이다.
입력 또는 출력의 순서가 스택 또는 큐와 같이 정해져있지 않기 때문에, 원하는 부분에서 먼저 출력을 할 수 있고, 이로인해 시간복잡도는 O(1)로 굉장히 효율이 좋은 자료구조이다.
3. Linked List - 연결 리스트
동적 배열의 구조를 갖는 자료구조의 연결 리스트는 각각의 list들을 연결 해주는 개념으로 볼 수 있다. 노드가 데이터 밸류 칸과 주소 칸으로 나뉘어져 있기에, 앞뒤의 list들을 연결하는 방식으로 배열을 꾸린다.
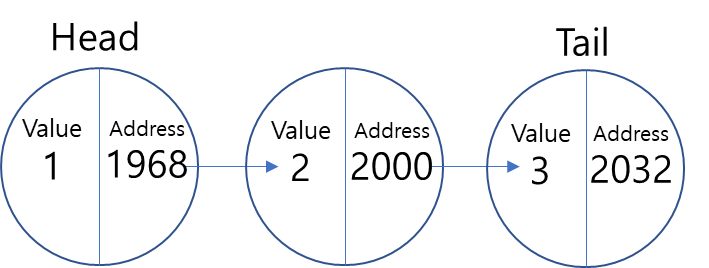
위 연결리스트의 이미지를 보면 노드가 왼쪽에는 값을, 오른쪽엔 주소값을 가진것을 볼 수 있다.
위와 같은 노드들의 주소값이 다음 노드의 주소값으로 '연결'이 되어 배열을 형성하는 것이 연결리스트 구조이다.
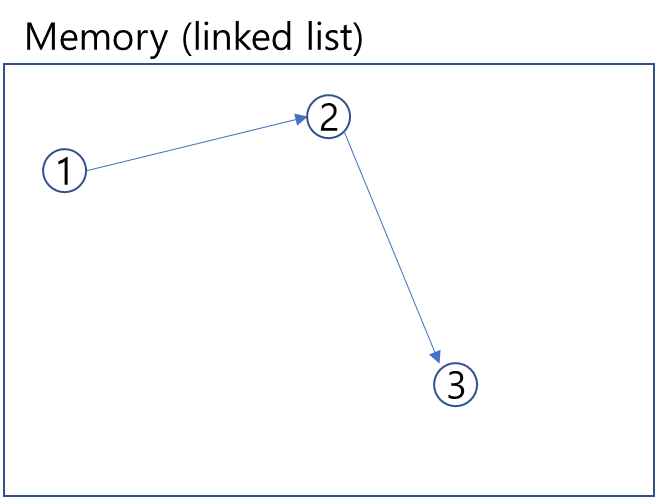
각각의 노드는 메모리에서 위 이미지와 같이 따로따로 저장되어있으며 각각의 주소를 뒷 노드에 이어주는 방식으로 이루어져있기 때문에 저장, 삽입과 삭제에 있어서는 굉장히 자유롭다.

파이썬의 List자료형에서는 각 노드들이 index를 통해 값을 찾을 수 있게 지정되는데, 메모리에서의 할당 역시도 위 이미지와 같이 데이터들이 붙어서 저장된다.
연결리스트
- 맨 첫 노드는 head, 맨 마지막 노드는 tail이라고 한다.
- 저장 공간적인 면이나, 삽입, 삭제 면에서는 파이썬 리스트 자료형보다 효율적이다.
삽입시에는 두 노드 사이에 노드를 삽입한뒤 포인터(주소) 연결만 고쳐주면 되며, 삭제도 동일한 과정으로 손쉽고 빠르게 진행 가능하다. 그러므로 삽입, 삭제에 관련된 시간복잡도는 O(1)로 단순 연산으로 진행된다. - 탐색에 있어서는 파이썬의 리스트보다 비효율적이다.
파이썬 리스트는 Index를 통해 단번에 값의 위치를 찾을 수 있지만, 연결리스트의 경우 head로부터 시작해 탐색해 나아가야 하기 때문에 최악의 경우 n번을 모두 확인해야할 수 있다. O(n)의 복잡도.
class Node:
def __init__(self, value, next=None):
self.value= value # 노드의 값을 나타내는 value
self.next= next # 노드의 다음위치를 가리키는 next. 초기값이 None
class linked_list:
def __init__(self, value):
self.head = Node(value) # 초기 클래스에 head 선언. 첫번째(헤드의) 값이 주어진다.
def add_node(value): # 노드를 추가하는 함수
node = head # 첫번째 위치에 해당하는 head를 생성한 뒤, node변수에 저장해둔다.
while node.next: # node.next가 None아닐떄 (add_node를 두번 이상 했을때를 의미) 반복문 진행
node = node.next # node 변수에 다음 노드를 넣어준다.
print('print in while:', node.next)
node.next = Node(value) # 데이터를 노드 다음 위치로 저장
link = linked_list(30) # 먼저 헤드에 30을 입력해본다.
link.add_node(13) # 이후 노드를 추가하면 뒷쪽에 붙는다. (삽입이 아니다)
link.add_node(15) # 하나 더 붙인뒤 확인해본다.
print(link.head.value) # 헤드값 출력
print(link.head.next.value) # 헤드 다음값 출력
print(link.head.next.next.value) # 고 다음값 출력[output]
30
13
15위에 간략이 연결리스트 구조를 코드로 구현해봤다. 삽입 및 삭제는 삭제한 뒤 next를 이어주면 된다. 다음으로는 본격적인 탐색에 대한 자료구조 및 알고리즘을 포스팅 해보도록 하겠다.