CS - 정렬 알고리즘 정리 및 구현 2 (분할정복: 퀵-Quick, 병합-Merge)

분할정복 알고리즘(Divide and Conquer)

복잡하거나 큰 문제를 여러개로 나눠서 푸는 방법.
작은문제로 나누어 해결한 뒤 합치는 과정을 거친다.

분할정복의 원리

• Divide-분할: 본문제를 여러 서브문제로 나눈다. 문제를 해결하기 수월하도록 작은 문제로 만든다.
• Conquer-정복: 문제를 최대한 분할 해야하며, 더이상 분할이 불가능 하면 문제를 해결한다. 분할된 문제들을 해결한다.
• Merge(combine)-병합: 해결한 문제들을 통합해 기존의 문제를 해결한다.

분할정복의 특징

• 어려운 문제를 작게 나누어 쉽게 해결한다.
• 작은 문제를 분할해 같은 작업을 더 빠르게 처리 가능하다
• 함수를 재귀적으로 사용해 오버헤드가 증가할 수 있다.

분할이 가능한지, 분할정복 알고리즘을 이용하는 것이 효율적일지를 생각해보고 사용해야 한다.

퀵 정렬(Quick Sort)

분할정복을 이용한 정렬 방법 중 피벗(pivot)과 파티션(partition)을 이용해 분할한 뒤 정렬하는 방법.
실제 사용빈도가 높은 알고리즘 중 하나로 버블, 삽입, 선택정렬보다 효율적이다.

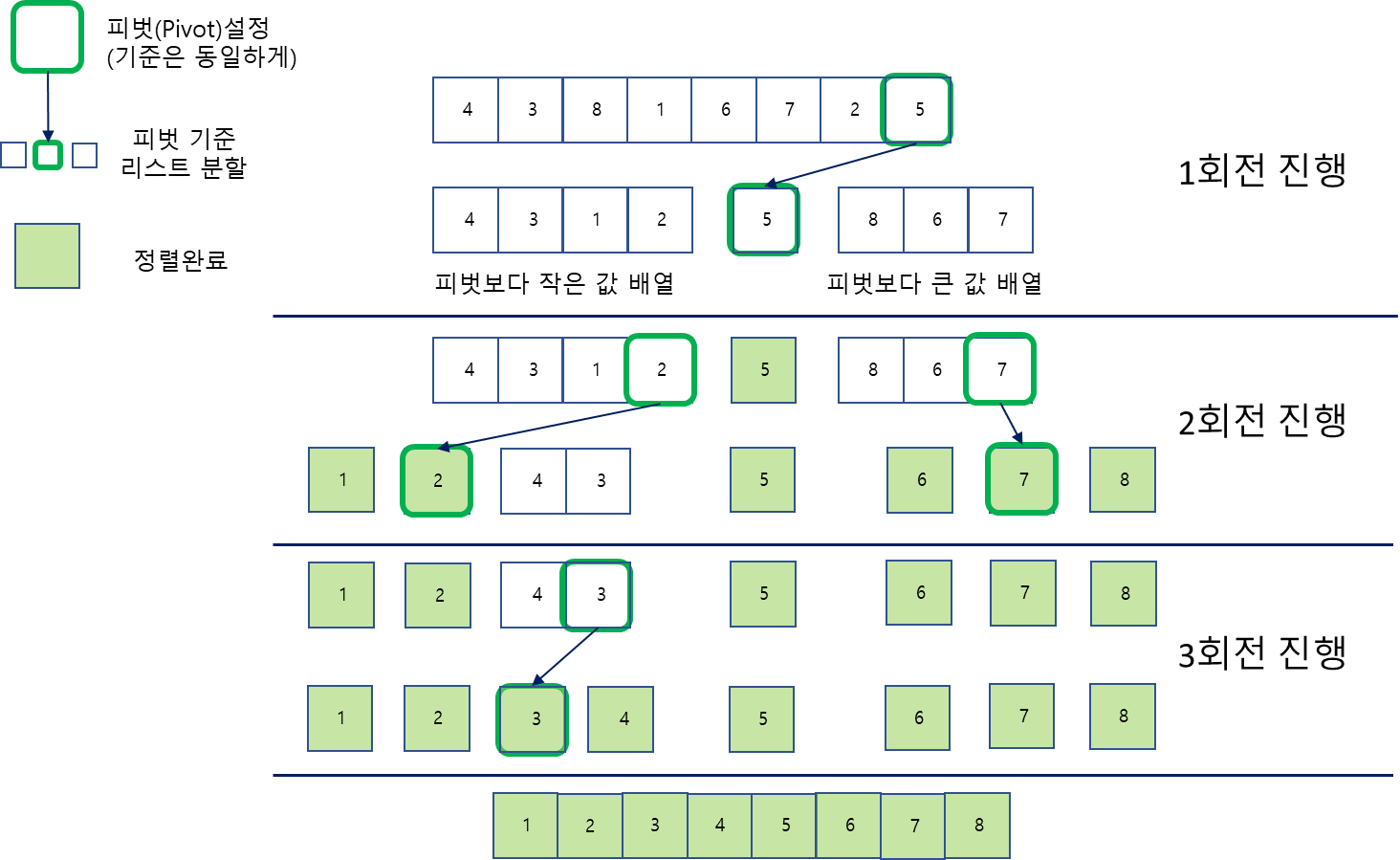
• 분할정복의 개념을 이용한 알고리즘, 점차 분할하여 정렬해나간다.
• 피벗(pivot)을 이용한 알고리즘으로 피벗은 분할을 위한 기준점을 의미
• 파티셔닝(partitioning)을 이용해
  * 이 피벗을 정하는 기준은 그 다음 분할에서도 바뀌어선 안된다.
• 이후 재귀적인 호출을 수행해 반복하여 정렬을 진행한다.

퀵 정렬 구현

def quick_sort(lst):
  
  if len(lst) <= 1: # 재귀를 통해 리스트 원소가 1개가 되면 그대로 해당값 반환
    return lst
  else:           
    pivot = lst[0]  # 피벗을 0번 인덱스로 지정
    greater = [i for i in lst if i > pivot]  # 피벗보다 큰 경우 greater 변수에 리스트로 넣는다.
    smaller = [i for i in lst if i < pivot]  # 피벗보다 작은 경우 smaller 변수에 리스트로 넣는다.
    return quick_sort(smaller) +[pivot] + quick_sort(greater) # 재귀함수를 통하 작은것부터 결과 리스트를 합쳐낸다.

lst = [4,7,1,6,3,2,9,0,8,5]
quick_sort(lst)

[output]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

• 선택정렬처럼 불안정 정렬에 속하므로 같은 값이 있더라도 내부적으로 재배치를 하는 정렬
• 배열 내에서 피벗이 균형잡힌 분할을 할 수 있는 값이어야 Best이다.
• 평균적인 시간복잡도는 $O(nlogn)$이며, 최악일 경우 초반에 완전히 불균형하게 하나씩 분할해야하므로 시간복잡도는 $O(n^2)$이 된다.
• H/W적인 영향을 받기 때문에 성능적으로 편차가 있을 수 있다.
  넓은 범위에서 움직이지 않아 지역성(locality)이 좋으며, 이로 인해 page-cache hit 비율이 높아 하드웨어적인 면에서 다른 정렬들보다 유리하다. 하지만 그로 인한 하드웨어적인 성능의 편차가 있을 수 있다.

병합정렬(Merge Sort)

합병정렬 또는 머지소트라고도 불리며, 이역시도 분할정복을 이용한 정렬방법이기에 큰 문제를 작은 문제로 나눈 뒤에 이를 해결하여 병합하는 방식을 취한다.

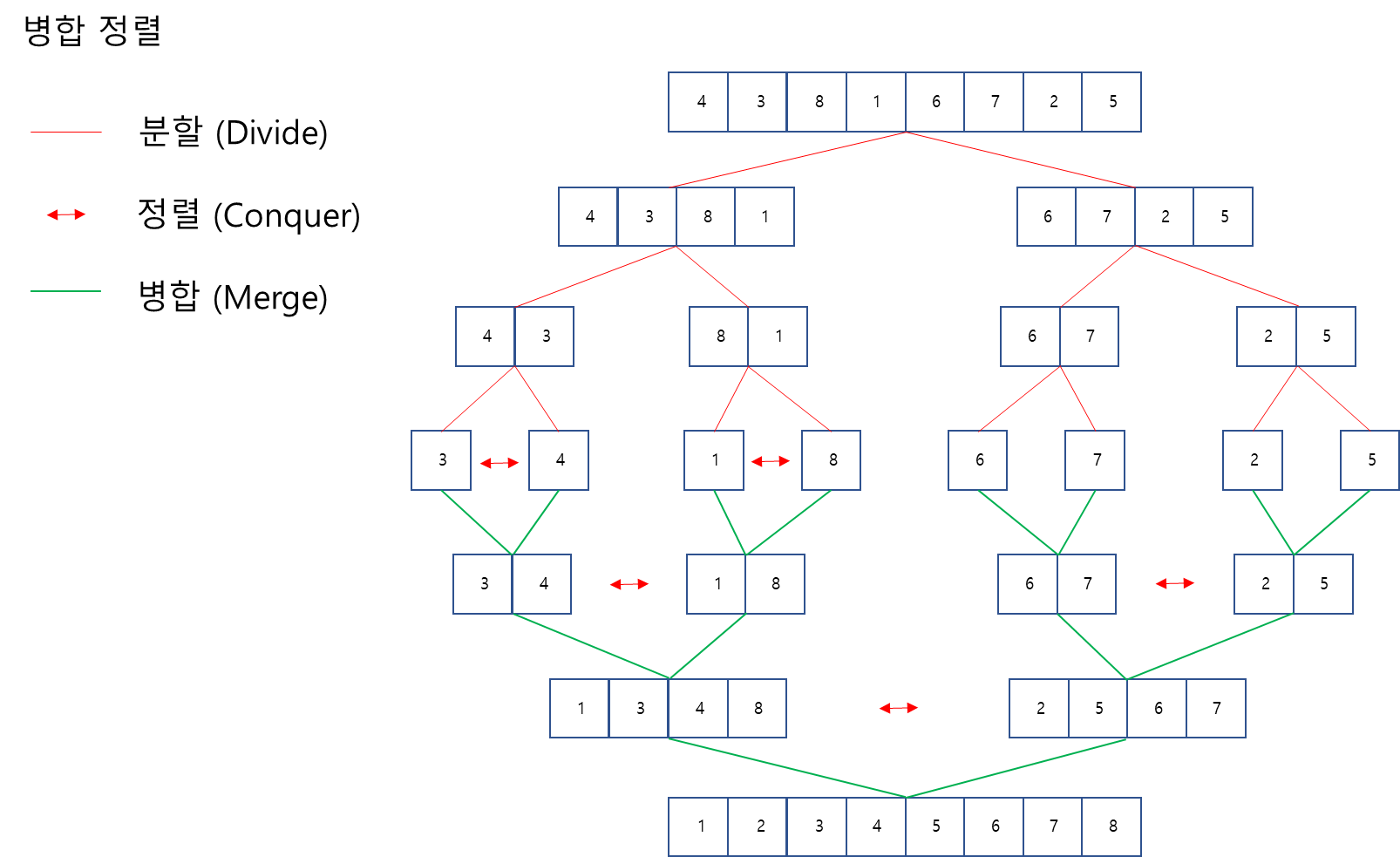
• 양분하여 분할한 뒤, 정렬하고, 병합을 하여 정렬하는 전형적인 분할정복법을 이용한다.
• 전체 데이터를 처음부터 끝까지 탐색한다.
• 따로 피벗이 존재하지 않아 이진분류 처럼 배열의 중간을 쪼개서 재귀호출로 반복을 진행한다.
• 병합을 할 때에도 정렬을 진행해야한다.

def merge_sort(lst):
  a = len(lst)      # 리스트의 길이
  mid = a //2       # 중간값
  if a >1:          # 길이가 1인 경우는 그대로 반환한다.
    L =  lst[:mid]  # 중간점 기준 left
    R = lst[mid:]   # 중간점 기준 right

    merge_sort(L)   # 분할이 될때까지 계속해서 재귀호출로 분할을 진행한다.
    merge_sort(R)
    
    i = j = k = 0        # 분할이 완료된 후 작업진행
    while i < len(L) and j < len(R):  # L과 R의 각각의 원소들을 반복 비교해 정렬해나가면서 병합한다.
      if L[i] > R[j]:    # L의 i번쨰 원소가 R의 j번째 원소보다 클 경우
        lst[k] = R[j]    # lst의 k번째 원소를 R의 j번째에 있던 가장 작은 원소로 맞춰놓는다.
        j += 1           # j번째는 리스트에 넣었으니 그다음 원소와 비교를 위해 j에 1을 더해 반복문 진행
      elif L[i] < R[j]:  # 위와 반대로 진행
        lst[k] = L[i]
        i += 1
      k += 1             # 반복 1회마다 메인 리스트에 원소를 넣었으니 그 다음 원소에 넣을 수 있도록 1을 더해줌
    
    while i < len(L):    # 연산 진행 후, L 또는 R이 불균형해 한쪽 리스트가 남아있을 때,
      lst[k] = L[i]      # 해당 리스트 원소들은 이미 반대편 리스트보다 큰 값이므로 반복문으로 넣어준다.
      i +=1
      k += 1
    
    while j < len(R):   # L과 마찬가지
      lst[k] = R[j]
      j +=1
      k += 1

• 분할이 불가능할 때까지(lst 길이가 1이 될때까지) 재귀호출을 계속해서 진행한다.
• 병합하는 과정에서 각 원소들의 비교를 한 뒤 정렬을 해야한다.
• 입력데이터가 많아지면 이동이 많아져 효율이 떨어지게 된다.
• 데이터의 분포에 따른 영향이 적다. 언제든 시간복잡도는 $O(nlogn)$
• 연결리스트로 구성할 경우 굉장히 효율적일 수 있다.