Learning rate, Overfitting, 규제화

Learning Rate

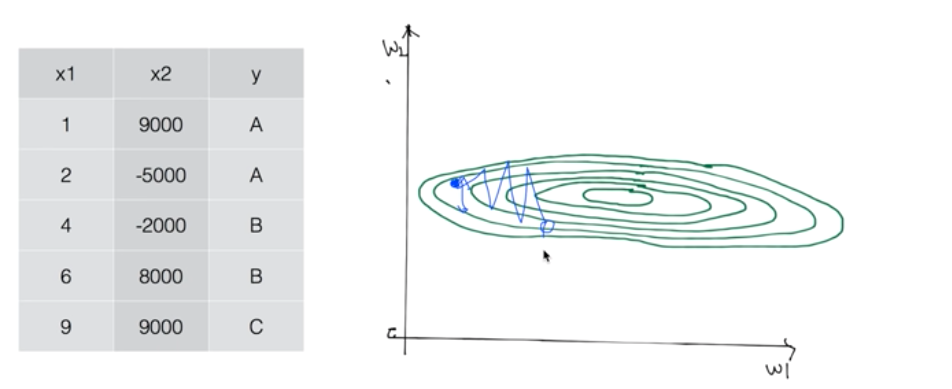
• Gradient decent 알고리즘에서 경사를 따라 내려오는 step의 정도로 큰값이면 속도는 빠르지만 정확도가 떨어지고 작은 값이면 그와 반대로 느리지만 정확도는 올라간다. 따라서 데이터 환경에따라 어떤 값을 적용해야할지는 다르며 케이스별로 임의의 값을 넣어본 후 적당한 값을 찾아야한다.
  아래와 같이 x1, x2의 데이터 값이 큰 차이가있다면 이에 곱해지는 가중치 행렬 w역시 차이가 있을 것이다. 따라서 꽤 괜찮은 learning rate 값임에도 불구하고 예측값이 발산할 수 있다. 이런 경우에는 데이터의 nomarlize 과정이 필요하다.
  
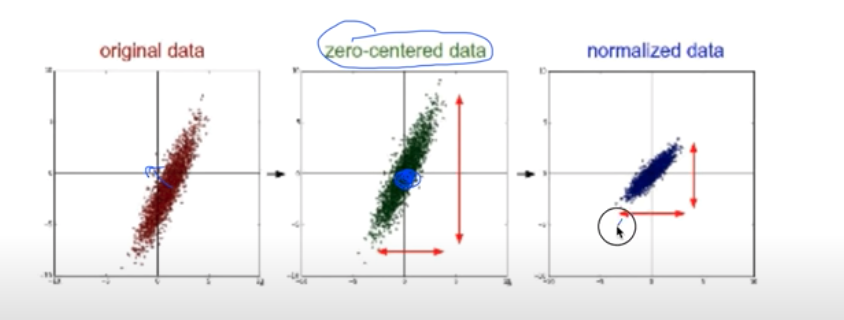
• Zero-centered data : 데이터의 중심을 원점으로 옮기는 방법
• Normalized data : 데이터를 평균과 표준편차를 이용해 normalize하는 방법
  

Overfitting

• 머신러닝은 학습데이터를 통해 모델을 만들고 실제데이터와 가장 근접한 결과를 예측한다. 하지만 학습데이터에 너무 만족하려고 fitting할 경우 그 학습 데이터로는 매우 근접한 결과를 예측하지만 추가로 다른데이터를 넣을 경우는 오히려 실제와 벗어난 예측을 할 수 있다. 즉, 아래와 같이 model2에서 처럼 학습데이터를 완벽하게 modeling하다보면 일반적이지 않은 모델이 만들어져 다른 데이터에는 맞지 않게된다.
  
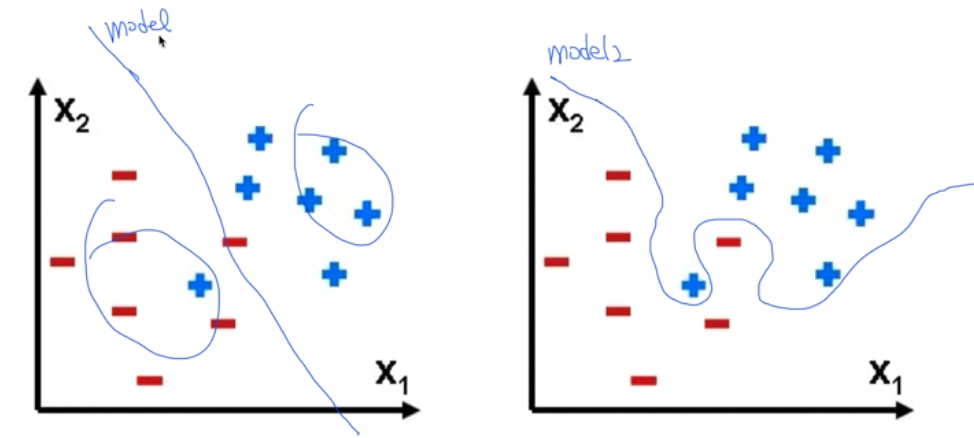
  따라서 overfitting을 최소화하기 위해서는 아래의 방법들이 있다.
• training data set을 늘린다
• training data의 중복된 feature를 제거
• 규제화(regulalization)

Regularization

• 모델이 overfitting을 일으킬 경우 이를 개선하기위해 사용하는 방법이다.

• 위의 model2 그림을 보면 데이터를 설명하기위해 선을 엄청 구부렸다. 이은 예측 함수가 매우 고차함수임을 의미하기 때문에 이 함수의 계수값들인 W(가중치)값을 줄여줌으로써 model1처럼 펴주는 작업을 해줄 수 있다.

• 아래 식을 보면 기존의 cost function뒤에 λ가 있는 항이 추가된 것이 보인다. 이 λ를 regularization strength라고 부르며 이 값을 조절해서 규제화를 한다. λ값은 또한 hyper parameter라고 불리며 모델을 적용할 때 적절한 값을 대입함으로써 손실함수를 최소화하는 값을 찾으면 된다.

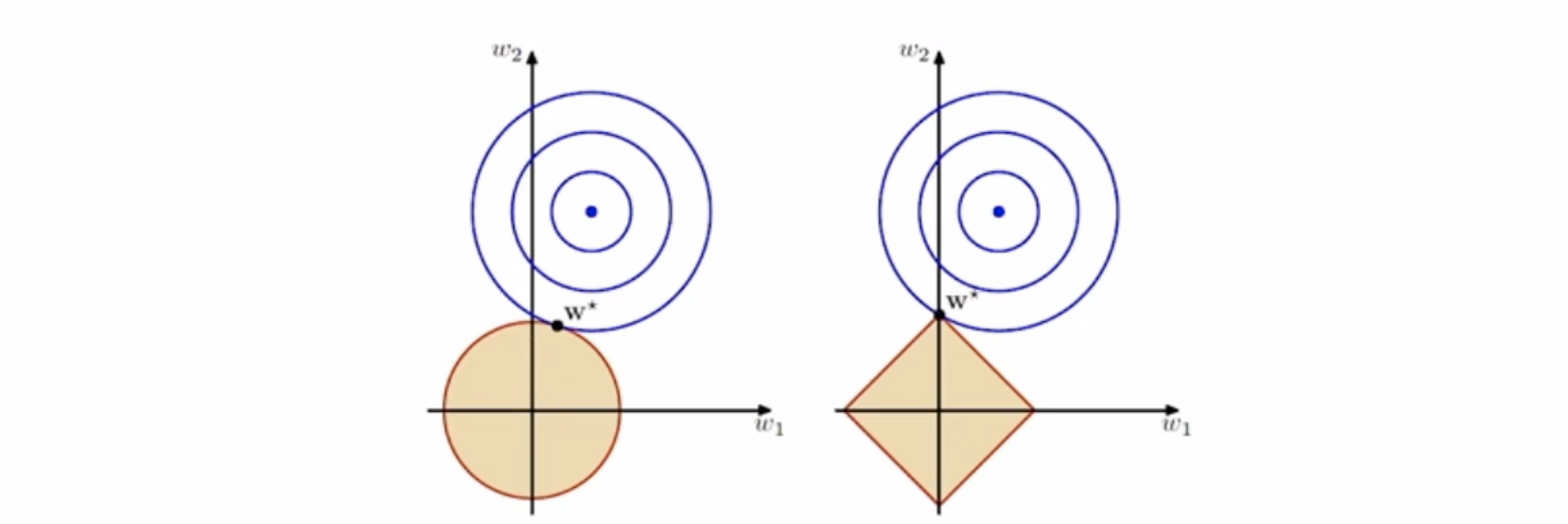
• 규제화의 방법에는 L1(Lasso regularization)과 L2(Ridge regularization)이 있다. 각각 L1은 1차식의 절대값, L2는 제곱의 절대값의 norm(벡터의 길이) 형태로 주어진다.
  

• W1과 W2만 있는 경우를 가정해 그래프로 표현하면 아래와 같다. 왼쪽은 제곱의 형태인 L2이고 오른쪽은 1차식의 형태인 L1이다. 따라서 Lagrangian 승수법(제약이 있는 경우 최적해를 구하는 방법)을 적용하면 이 규제화 항을 제약조건으로 보고 손실함수(아래그림에서 동심원)를 최소화시키는 해를 구할 수 있다.