Logistic Classification
연속적인 값을 예측하는 선형회귀 분석과는 달리 분류 문제가 주어졌을 때는 특히 둘중하나를 고르는 binary의 경우에는 Logistic Classification를 사용한다. Logistic Classification 모델은 뒤에서 배우게될 Neural Network의 기본이라고도 할 수 있으므로 제대로 이해하는 것이 굉장히 중요하다.
1. Logistic Classification를 사용하는 이유
우선 Logistic Classification 모델을 사용하는 이유에대해서 알아보자. 아래 그림과 같이 공부한 시간에 따른 시험의 합격(pass)/ 불합격(fail) 여부을 예측하는 모델을 생각해보자.
만약 아래 경우를 모델링하기위해 선형회귀 모델을 사용한다면 그림 맨 오른쪽과 같은 이상점이 발생할 경우 그림처럼 이상점까지 잘 예측하기위해 선형식의 기울기는 누워진다. 결국에는 합격과 불합격을 나누는 y축상의 기준을 0.5라고 했을 때 기울기가 누워지면 그 기준이 그림처럼 오른쪽으로 옮겨지게되어 정확하게 예측하지 못하는 경우가 발생하게된다. 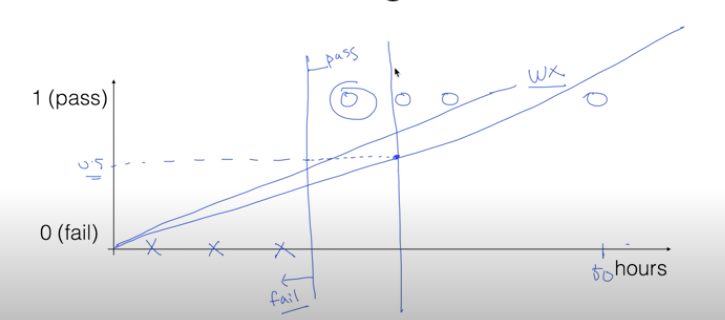
또한 binary 분류모델에서 우리가 원하는 결과값은 0또는 1이면 충분하다. 하지만 선형회귀 모델은 입력에따라 예측값 또한 선형적으로 증가하므로 굉장히 크게 나올 수 있다.
따라서 이 결과를 특별함 함수를 사용하여 0 ~ 1사이의 값으로 정규화 해준다. 이 때 사용하는 특별한 함수를 바로 Logistic function 또는 Sigmoid function이라고 부르며 아래와 같이 표현된다.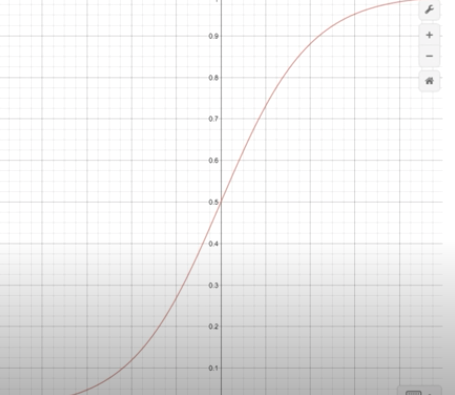
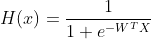
2. Logistic Classification의 손실함수(Cost Function)
Logistic Classification 모델의 손실함수는 선형회귀 모델과 동일한 함수를 사용한다고 가정하고 예측함수(H(x))를 분모가 지수함수인 sigmoid 함수를 적용한다면 오른 그림과 같은 울퉁불퉁한 형태로 표현이 된다는 문제가있다. 이 경우 손실함수가 최소인 값을 미분을 이용해 구하기가 어렵다. 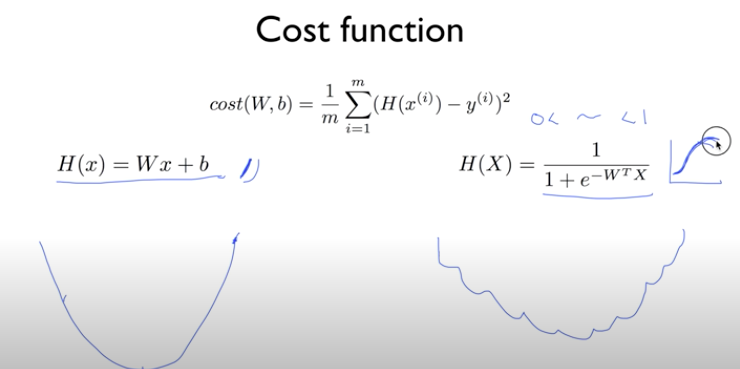
따라서 지수와 로그함수는 반대의 성질을 가진다는 특성을 이용해 울퉁불퉁한 함수를 쫙쫙 펴줄 수 있으며 결국에는 로그를 이용해 손실함수를 표현함으로써 위 문제를 해결할 수 있다.
아래 손실함수에서 항이 두개인 이유는 y(목표값)이 0과 1인 분류문제에서 y가 0인경우 왼쪽항이 0으로 사라지고 1인경우 오른쪽항이 사라지는 효과를 낼 수 있기 때문이다.
마지막으로 우리의 목적인 손실이 최소가 되는 최적의 값 W를 구하기위해서는 손실 함수를 W에 대해 미분함으로서 쉽게 구할 수 있다.
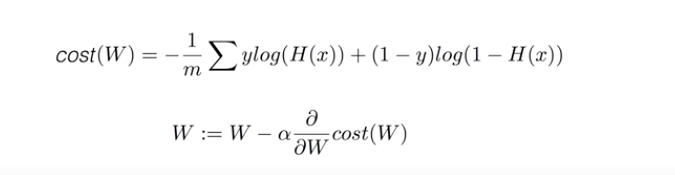
여러개의 class가 있을 때 사용하는 Multinomial Classification, 그 중에서도 가장많이 사용하는 것이 Softmax Classification이다. 따라서 Softmax Classification를 잘 알기위해서는 Multinomial Classification 먼저 이해해야한다.
Softmax 함수
1. Softmax 함수를 사용하는 경우
지난 시간에 Logistic Classification에서 예측값을 binomial(0 또는 1)로 mapping을 했었는데
Multinomial Classification는 아래(A,B,C)와같이 여래개의 예측값으로 mapping을 하는경우이다.

즉 binominal인 경우는 sigmoid 함수를 사용해 0~1사이의 값으로 mapping 했지만 Multinomial에서는 Softmax라는 함수에 예측함수의 결과를 통과시킨다.

2. Softmax 함수의 의미
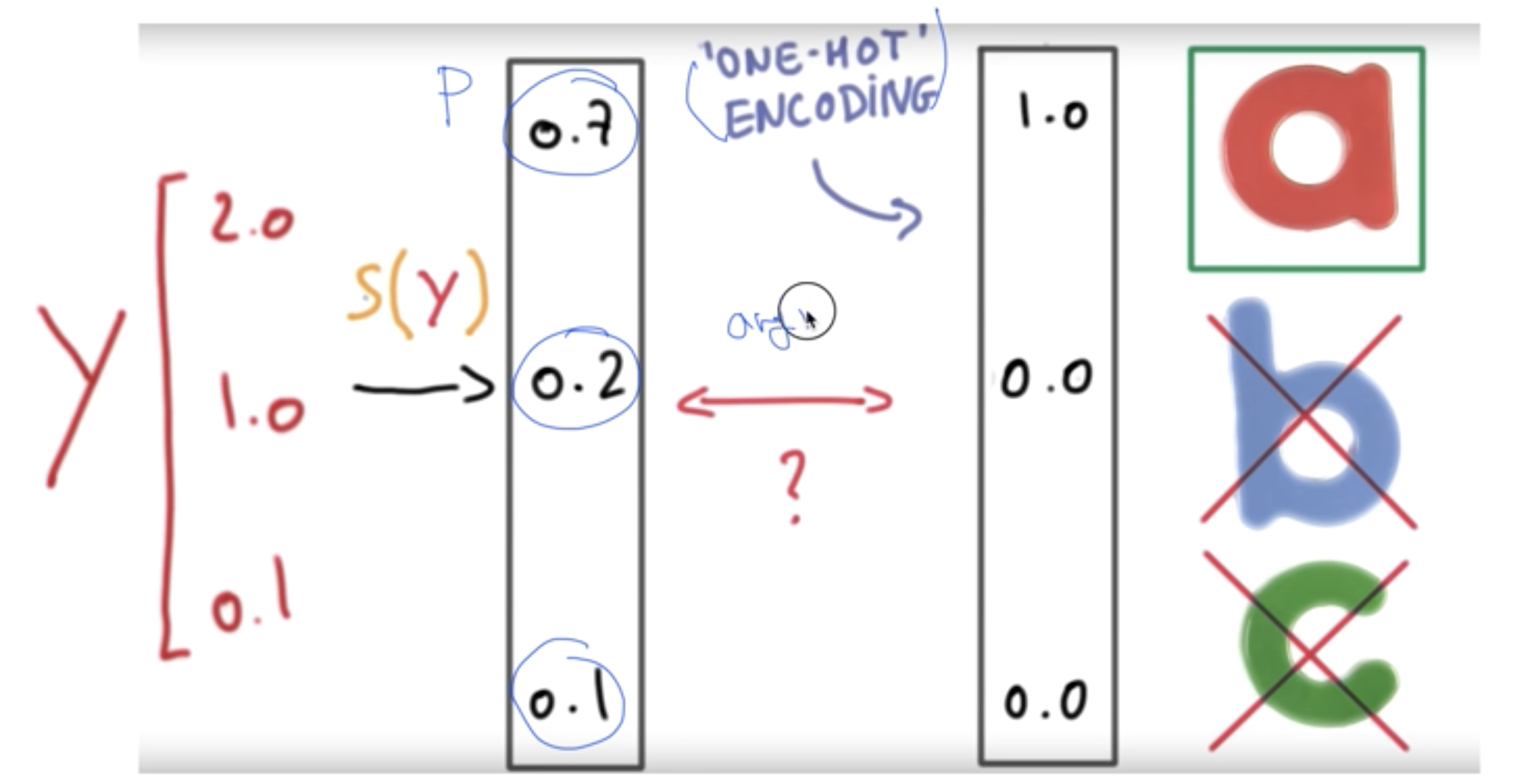
Softmax는 sigmoid 함수와 유사하게 결과값이 0~1사이로 출력이 되지만 한가지 다른점은 그 결과 값들의 합이 마치 확률처럼 1이 된다는 사실이다. 따라서 Softmax를 통과해서 나온 결과는 어떤 입력이 들어갔을 나오는 예측값에대한 확률이라고 볼 수 있다.

참고로 이렇게 출력된 확률을 0또는 1로 바꿔주는 테크닉이 있는데 이를 one-hot encoding이라고한다.
3. Multimomial에서 손실함수
Multinomial인 경우 손실함수(Cost-function)를 최소화, 최적화(?)하기위해서 Cross-Entropy라는 함수를 사용한다.
Entropy가 확률에서 사용될 때는 자기정보의 평균을 의미하며 자기정보란 어떤 사건이 일어날 확률의 역수에 로그를 취한 값으로 역수이므로 확률이 낮을 수록 그 사건이 가진 정보는 크다고 볼 수 있다.

Cross-Entropy함수에서 Li는 실제값이며 Si는 예측값이다. 그리고 이 예측값에 -log를 취하고(위에서 말한 자기정보의 형태이다) 실제값을 곱해주면 아래와같이 실제값과 예측값이 맞을 때는 0, 틀릴 때는 무한대를 결과로 내주어 맞을 때와 틀릴 때의 값을 확실이 구분해준다. 이 것은 예측값이 로그함수를 통과 하면서 0 또는 무한대의 값을 출력해주기 때문이다.

실제 Cross-Entropy함수가 아래와 같이되며 실제값(y)이 0또는 1일 때 예측값 H(x)의 값에따라 결과가 어떻게 달라지는 확인해보면 왜 이런함수로 정의되었는지 알 수 있다.

여러개의 Training set인 경우에서는 아래와같이 손실함수가 주어진다. 즉 손실함수는 각 예측값의 cross-entropy함수에대한 결과를 평균한 값이다.

마지막 과정은 Linear Regression이나 Logistic Classification과 마찬가지로 Gradient descent를 이용해 learning rate를 지정하여 경사를 따라 손실이 최소가 되는 값을 찾는 과정이다.