Machine Learning 이란?

• 경험을 통해 자동으로 개선하는 컴퓨터 알고리즘의 연구
• 학습데이터를 통해 목표값을 예측하는 함수
  

다항식 곡선 근사(polynomial curve fitting)

• 학습데이터 : 입력벡터 X와 목표값벡터 t
• 목표 : 새로운 입력벡터가 주어졌을 때 목표값을 예측하는 것
• 확률이론 : 데이터에는 기본적으로 노이즈가 섞여있어 예측값의 불확실성을 정량화시켜 표현하기위한 수학적 프레임워크를 제공한다.
• 결정이론 : 확률적 표현을 바탕으로 최적의 예측을 수행할 수 있는 방법론을 제공한다.
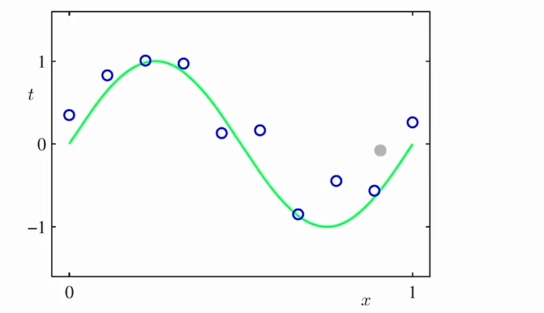
  다항식 곡선 근사함수를 다음과 같이 가정한다.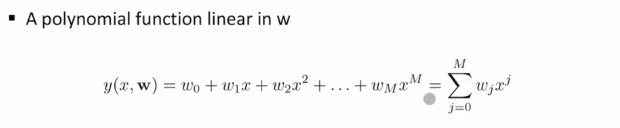이 때 입력은 x이고 목표값을 가장잘 예측하는 함수 y(x,w)의 계수들(w0,w1...)를 구하는 것이 과제이다.
  과소적합(under-fitting) : M이 작은 경우(0 또는 1) 학습데이터를 잘 설명하지 못하는 과소적합이 일어 날 수 있다.
  과대적합(over-fitting) : M이 너무 크면 학습데이터만을 잘 예측하고 새로운 데이터에대해서는 취약한 과대적합이 일어날 수 있다. 데이터가 많아지면 이러한 과대적합은 개선될 수 있다.

규제화(Regularization)

• 위에서 M이 큰 경우 과대적합이 일어날 수 있고 이러한 경우에는 계수 or 가중치 w이 값들이 매우 큰 값으로 나타날 수 있따. 따라서 규제를 통해 가중치(w)의 크기를 줄이거나 0으로 만들어 과대적합을 개선할 수 있다. 이러한 규제화 모델에는 L1, L2 Norm이 있다.
  L1 : 가중치들의 합에 λ를 곱한 후 손실함수(cost function)에 더해준다. L1에서는 λ 값에따라 가중치를 0으로 만들어 줌으로 해당 feature의 영향을 아예 배제할 수있다.
  L2 : 가중치들의 제곱합에 λ를 곱한 후 손실함수(cost function)에 더해준다. λ는 가중치의 크기를 조절하며 λ가 크게하면 규제를 크게주어 가중치가 작아지고 λ가 작을수록 규제가 작아져 원래 손실함수와 비슷하게 표현된다. L2가 L1보다 안정적이라 일반적으로 더 많이쓰인다고한다.
  

결합확률분포

• 결합확률(joint probability)는 확률변수(예를들어 X,Y)가 2개일 때 사건이 동시에 발생할 확률이다.
• 따라서 두사건의 교집합의 확률을 의미한다.
• P(X), P(Y)의 각각의 확률은 주변확률이라한다.
  결합확률의 확률변수의 분포를 결합확률분포라고하며 다음의 조건을 가진다.
  1) X, Y가 이산확률인 경우
  
  2) 연속확률인 경우