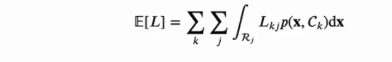결정이론(Decision Theory)

결정이론이란?

• 새로운 값 X가 주어졌을 때 확률모델 p(x,t)에 기반해 최적의 결정을 내리는 것
• 추론단계에서 결합확률분포를 구하고 결정단계에서 확률을 근거로 어떻게 최적의 결정을 낼지 정한다.
• 결합확률분포가 주어졌을 때 최적의 결정영역들을 찾는 것이 목표이다.

이진분류

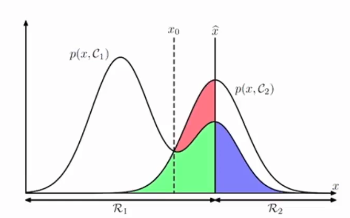
결정영역 Ri = {x : pred(x) = Ci}가 주어졌다고하자. 아래 결합확률분포 그림에서 분류의 기준을 x_hat이라고 했을 때 분류오류의 확률은 영역 R1에 속하는 x를 클래스 C2로 분류하고(빨간 + 녹색) 영역 R2의 x를 클래스 C1로 분류(보라)했을 때이다. 이 때 만약 분류기준을 x_hat에서 xo로 옮긴다면 빨간색 영역이 제거되면서 잘 못 분류된 영역이 최소가 된다. 따라서 p(x,C1) > p(x,C2)를 만족할 때 x를 영역 R1에 할당하면 오류가 최소화된다는 것을 직관적으로 생각할 수 있다.

Multiclass인 경우

클래스가 여러개인 경우는 오류보다는 얼마나 정확한지를 생각하는 것이 좋다. 따라서 결정영역 Ri와 클래스 Ci가 일치하는 확률을 모두 더해 얼마나 정확한지에 대한 확률을 구할 수 있다. 그리고 x가 주어졌을 때 조건부확률 p(Ck|x)가 최대가되는 영역 Rk에 클래스를 분류하면 정확도가 가장 높다고 볼 수 있다.

기대손실 최소화(Minimizing the Expected Loss)

• 모든 결정이 동일한 리스크를 갖는 것이 아니기 때문에 리스크의 정도를 구분하기위해 손실행렬(loss matrix)를 가정한다.
  • Lkj(손실행렬) : Ck에 속하는 x를 Cj로 분류할 때 발생하는 손실 또는 비용.
• 다음과 같은 기대손실을 최소화하는 것을 목표로한다.