퍼셉트론
사람의 뇌의 가장 기본단위인 뉴런을 본따 만든 것이 퍼셉트론이다. 딥러닝의 가장 기본적인 단위로 퍼셉트론을 순차 결합한 것을 다층 퍼셉트론이라고하며 다층 퍼셉트론을 병렬적으로 여러개 연결한 것을 깊은인공 신경망이라고 부른다.
퍼셉트론의 기본 구조
입력인 학습데이터와 매개변수인 가중치 곱을 모두 더한 후(내적과 동일한 연산) 그 결과가 비선형의 활성함수를 통과해 예측값을 출력하는 구조이다.

퍼셉트론을 기하학적으로 생각하면 아래와 같이 입력벡터 x[x1,x2]와 가중치벡터 w[1,1]의 내적을 파란색선인 결정직선으로 볼 수 있다. 만약 파란색 결정식선이 아래의 분류를 제대로 수행하지 못한다면 경사하강법을 이용해 w값을 갱신함으로써 결정직선의 위치를 수정해 보다 모델을 잘 예측하는 분류기가 될 수 있다.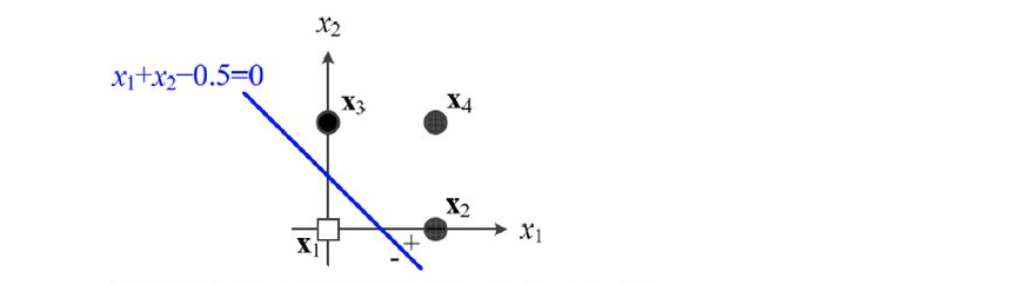
경사하강법에서 최적의 값을 찾기위해 손실함수를 미분한값은 벡터 w의 각각의 요소에대한 편미분 값들의 합이다.
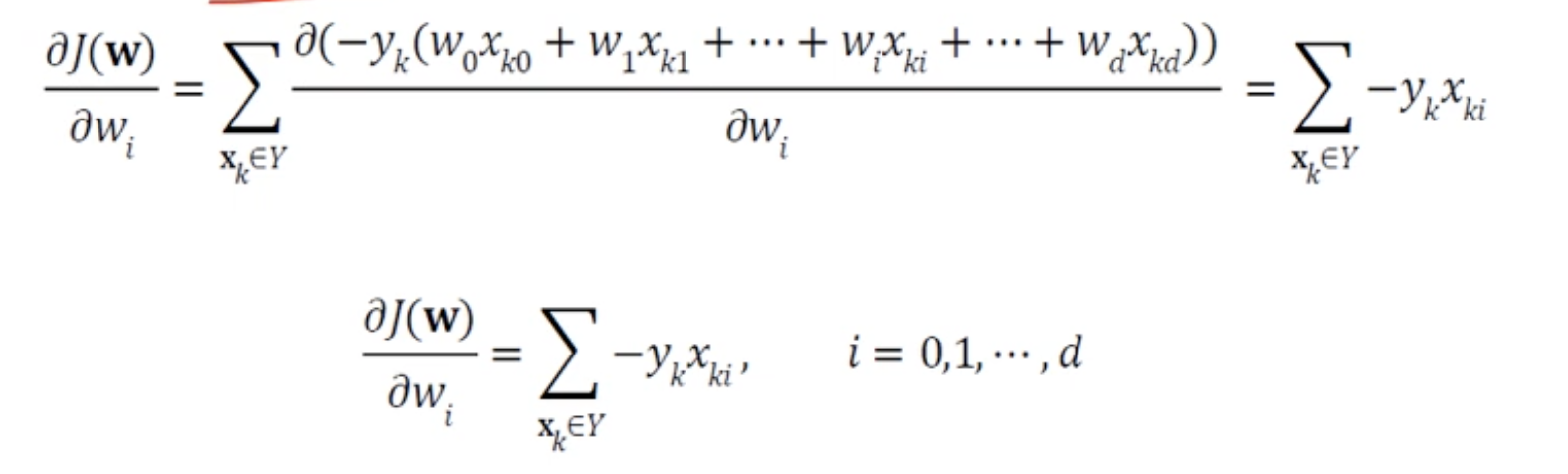
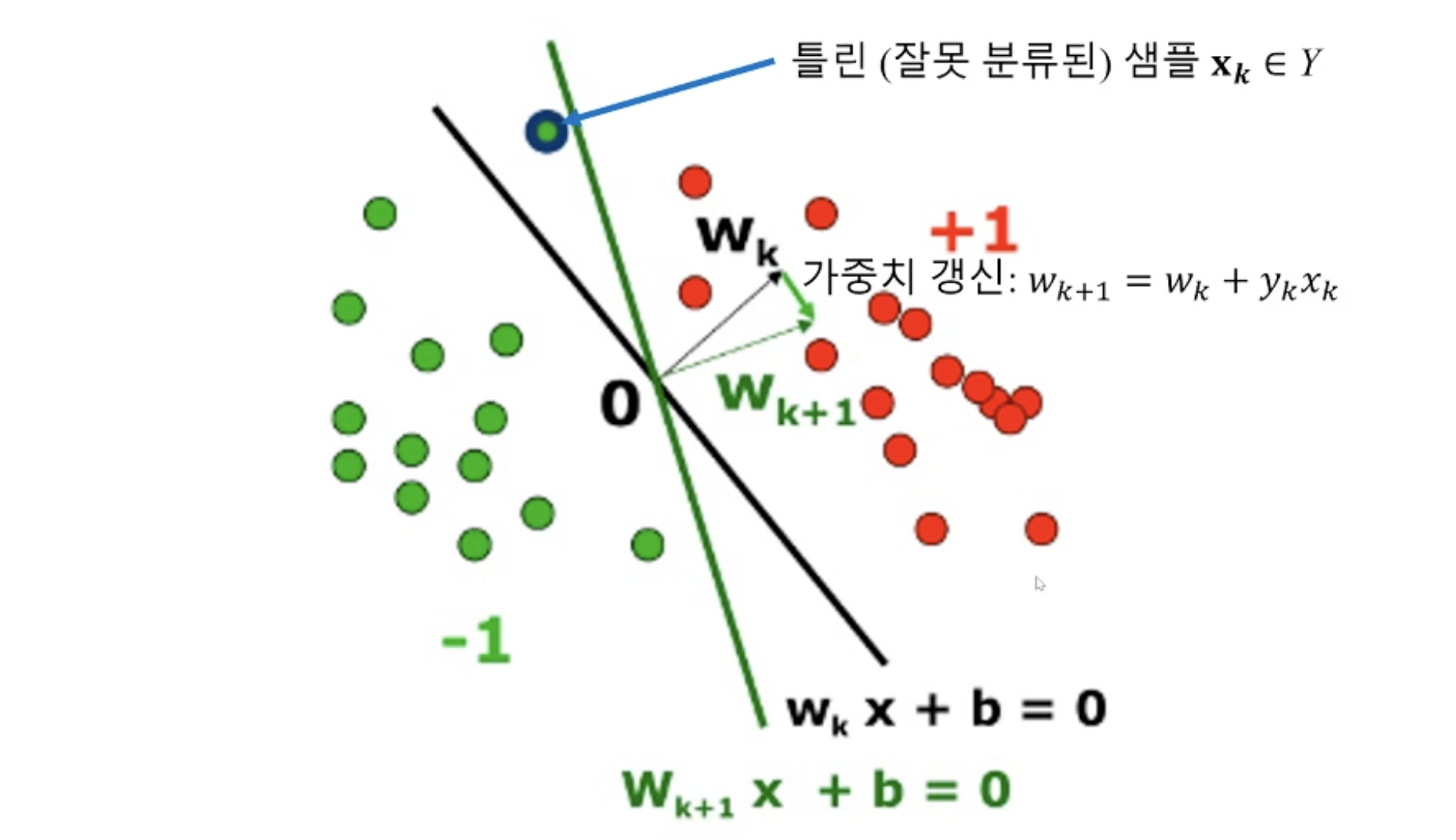
따라서 각각의 가중치는 아래 그림처럼 잘못분류된 입력(xk)과 실제값(yk)의 내적에 기존 가중치(wk)의 합으로 갱신된다.
다층 퍼셉트론
단순 선형분류기(단일 퍼셉트론)만으로는 XOR과 같은 논리를 구분하는데 한계가 있었다. 이를 해결하기위해 퍼셉트론을 다층구조로하는 모델을 제시하였고 이를 다층 퍼셉트론이라고 한다.
다층 퍼셉트론의 핵심 아이디어
- 은닉층(hidden layer)를 두어 원래 특징공간을 분류가 유리한 새로운 특징 공간으로 변환한다.
- sigmoid 활성함수를 도입하여 기존의 hard한 스텝함수(출력이 0 또는 1) 보다 soft한 결과(출력이 연속)을 가질 수 있게되었다.
- backpropagation 알고리즘을 도입하여 에러를 역방향으로 전달하여 각 layer의 가중치를 갱신하는 방식을 사용한다.
은닉층(hidden layer)
입력과 출력층 사이에 존재한다고해서 은닉층이라고하며 외부 시스템에서는 이를 실제로 볼 수 없다. 일반적으로 이러한 은닉층이 많을 수록 더 복잡한 문제를 푸는데 유리하며 각 층에서는 입력(그전 층의 출력)과 가중치의 행렬곱(선형변환)이 이루어지면서 공간의 변형이 일어나고 특징이 추출(가중치와의 내적에의해서)된다고 할 수 있다.
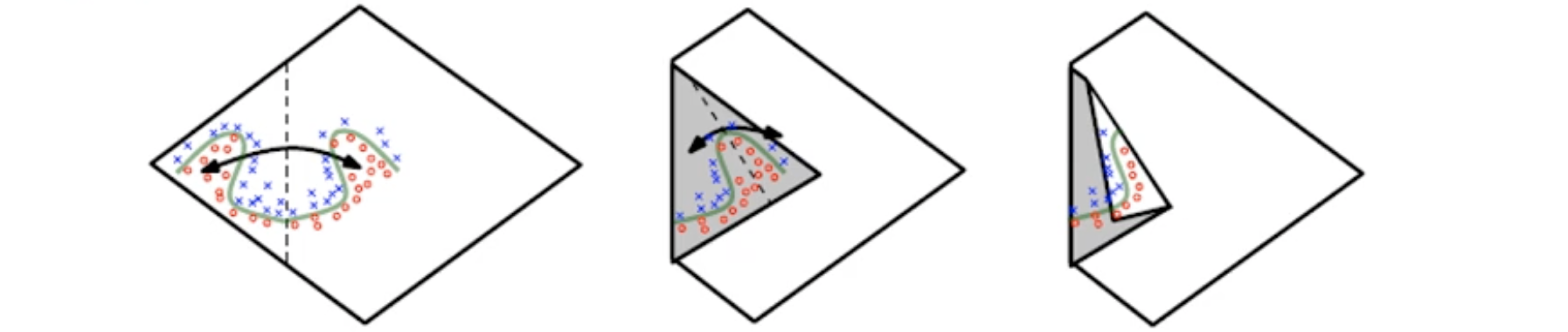
각 은닉층은 아래의 그림에서 입력 공간을 어디서 접을지 지정하는 것과 같다. 공간을 접으면 새로운 공간으로 변형이 일어나며 공간을 접으면 접을수록 원공간에서는 분류하기 복잡했던 것이 점점 더 심플하게 선형으로 분류가능해진다.
아래 그림처럼 단일 퍼셉트론 3개를 병렬적으로 배치한 구조에서 입력 x1,x2와 각 퍼셉트론의 가중치 w가 만드는 결정직선은 2차원 공간을 7개로 구분한다. 반면 퍼셉트론을 3개 사용했으므로 입력과 가중치의 내적의 결과는 z1,z2,z3가 되므로 원래 특징공간인 x[x1,x2]가 새로운 특징공간 z[z1,z2,z3]로 변환되었다고 볼 수 있고 7개로 구분된 각 영역은 3차원의 공간으로 매핑될 수 있다. 이렇게 새롭게 공간이 변형된다면 기존 2차원 공간에서는 쉽게 구분될 수 없었던 A지점이 변경된 3차원 공간에서는 보다 쉽게 선형분리 가능하다는 것을 알 수있다.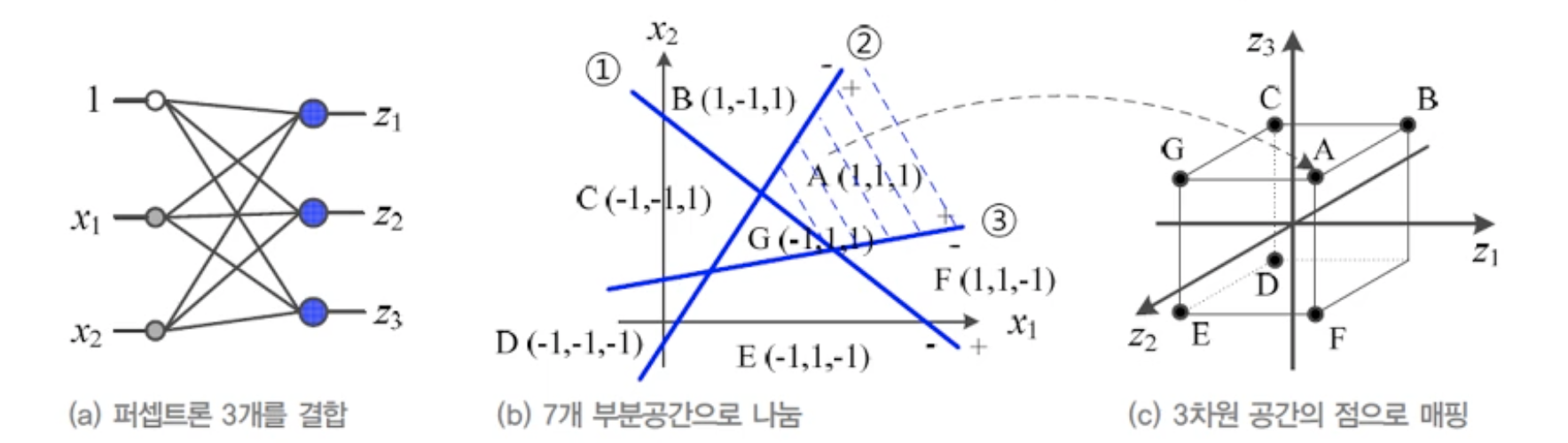
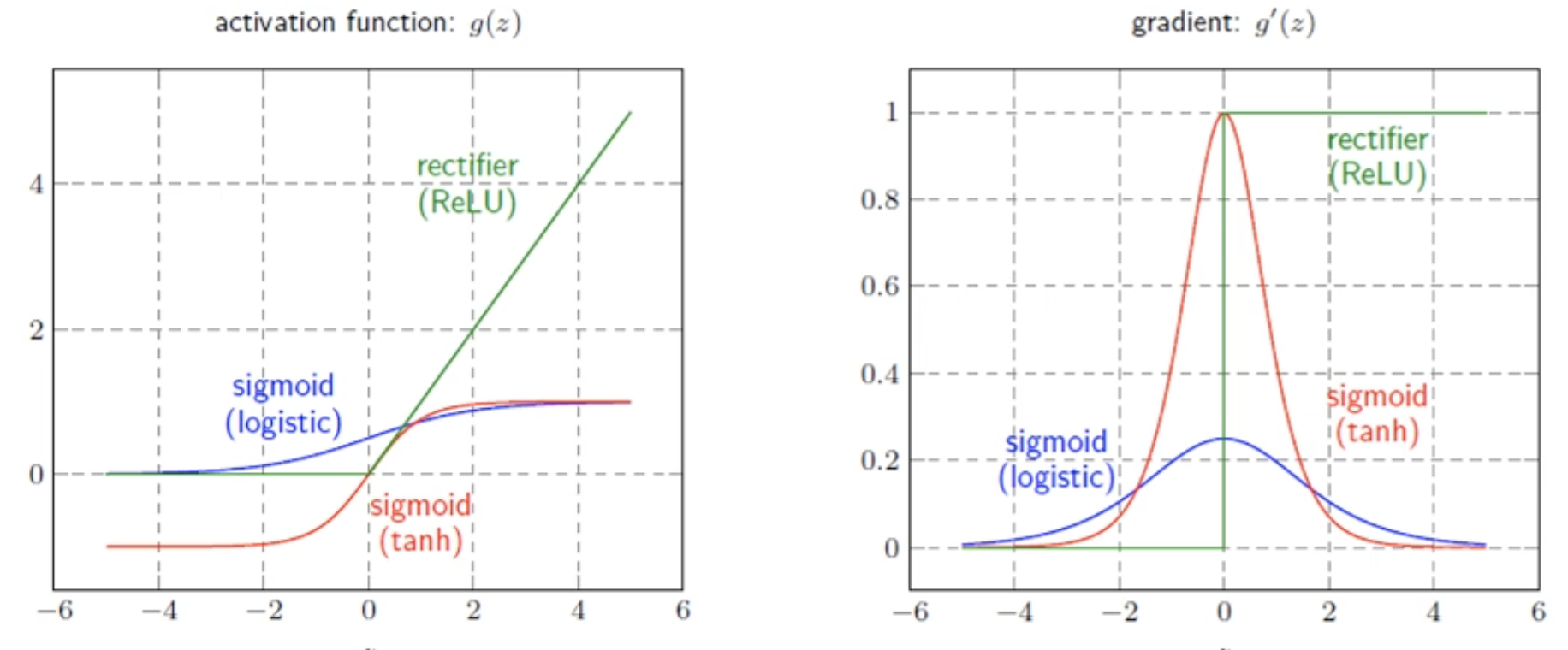
다층 퍼셉트론에서의 활성화 함수
단일 퍼셉트론에서는 활성화함수로 스텝함수를 사용했다면 초창기 다층 퍼셉트론에서는 sigmoid를 사용했었다. 여기서 초창기에 사용했다고 한 이유는 깊은 신경망에서는 가중치를 갱신할 때 backpropagation 알고리즘을 사용하는데 simoid 함수의 미분값이 아래 오른쪽 그림처럼 0에 가까운 부분이 존재하기 때문에 chain rule을 적용했을 때 에러가 전달되지 못하는 문제가 발생한다. 따라서 이를 해결하기위해 Relu(아래 녹색그래프)를 주로 활성함수로 사용한다.