다익스트라 알고리즘은 그래프의 최단 경로를 탐색하는 대표적인 알고리즘이다.

거리 정보에서 최솟값인 노드를 매번 취하기 때문에 그리디적인 방식과,
이전에 구했던 거리 정보를 이용하는 부분이 있어 다이나믹 프로그래밍적인 방식이 함께 사용된다.

기본 원리와 진행 방식

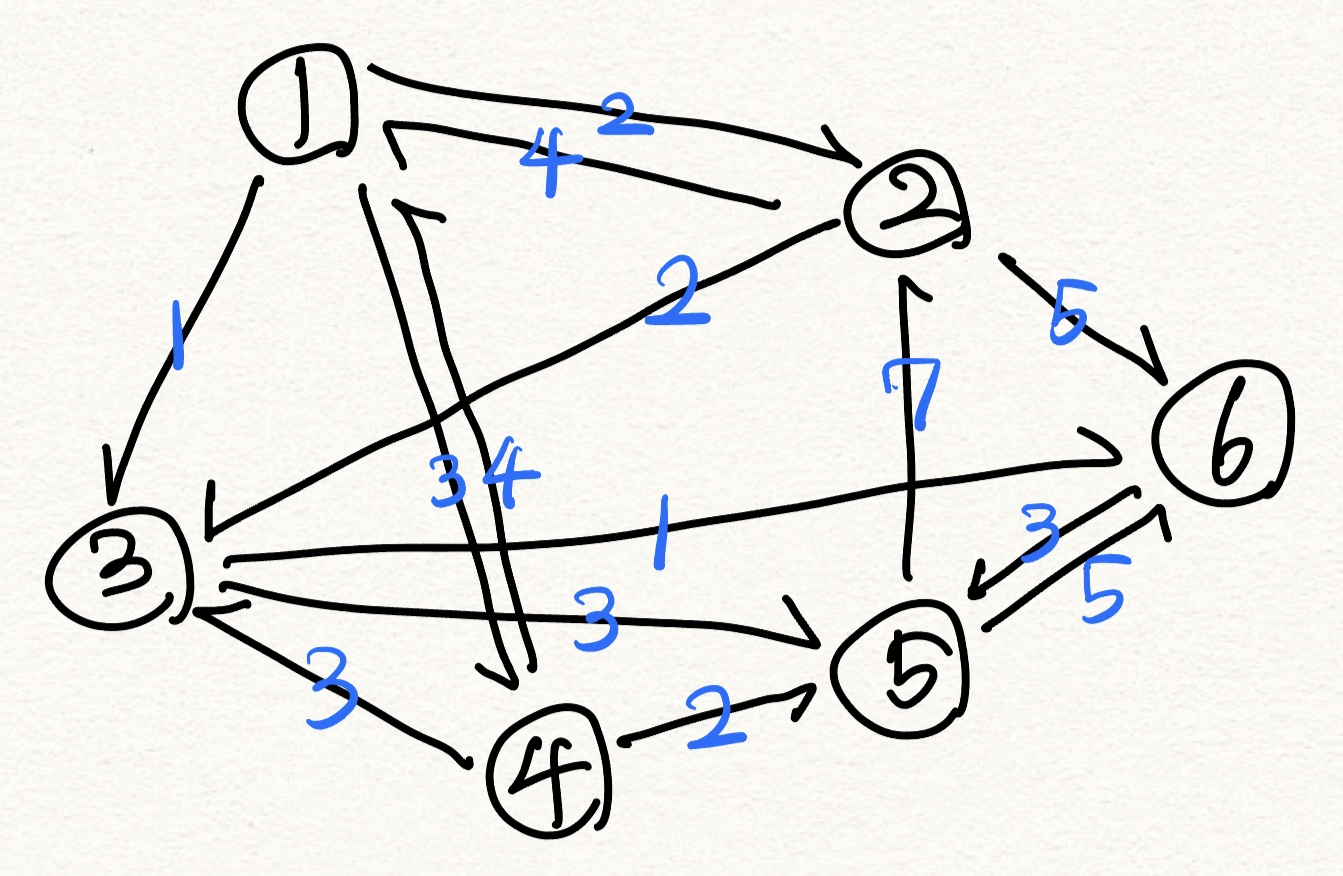
그림과 같은 그래프가 있다. 동그란 원은 노드이고 화살표는 간선이다. 화살표 위에 적힌 숫자는 거리(비용)이다.

1번에서 시작하여 모든 노드를 탐색할 때 최소 거리를 구하고자 한다.

먼저, 출발 노드를 기준으로 각 노드까지의 거리를 리스트로 만든다. 자기 자신의 거리는 0이고, 연결된 간선이 없으면 INF(무한대)로 한다.

그리고, 각 노드를 탐색하였는지의 여부를 또 리스트로 만든다.

최초 상황이니까 출발 노드만 True이다.

이제, 방문하지 않은 노드 중에서 최단 거리인 노드를 찾는다.

위의 케이스의 경우 거리가 1인 3이 될 것이다. 3을 방문한다.

이 때, 어떤 노드로 가는 데에 출발점에서부터 가는 경우보다 3을 경유해서 가는 것이 더 빠를 수도 있을 것이고, 원래 출발점에서 바로 갈 수 없었다가 3을 경유해서 갈 수 있는 경우가 있을 것이다. 지금 위의 그림에서는 1->5로 바로는 갈 수 없지만 1->3->5의 경로를 통해 갈 수 있다. 그렇다면 이런 경우를 다 포함하여 위의 거리 리스트를 새롭게 갱신해 준다.

이 때 거쳐가는 노드와 새 노드의 거리에다가 거쳐 가는 노드의 거리를 더해야 한다.

즉 a->b보다 a->c + c->b가 더 작을 때만 갱신해 주면 된다.

이제 3을 경유함으로써 5, 6번 노드에 갈 수 있게 되었다.

그리고 3을 방문했으므로 True로 만들어 준다.

그리고 방문하지 않은 노드들 중 최단거리 노드를 선택하고, 거리를 갱신하고, 방문을 체크하는 과정을 계속 반복한다.

한번 계속 해보자.

2로 가는거 2, 6으로 가는거 2가 가장 작다. 2를 고르자.

2에서는 1, 3으로 갈 수 있는데 갱신할 사항이 없다. 방문 여부만 True로 고쳐준다.

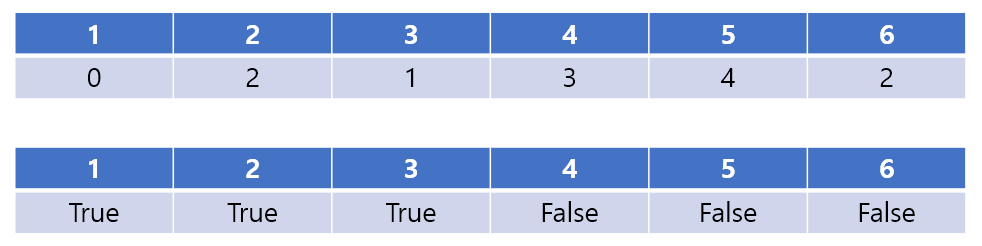
4, 5, 6 중에서는 6이 비용 2로 가장 작다. 6을 고른다.

6에서는 5로 갈 수 있는데 비용이 5이므로 마찬가지로 갱신할 사항이 없다. 방문 여부만 고쳐준다.

원래 갱신이 자주 돼야 하는데 그림을 잘못 그린 것 같다. 쩝...

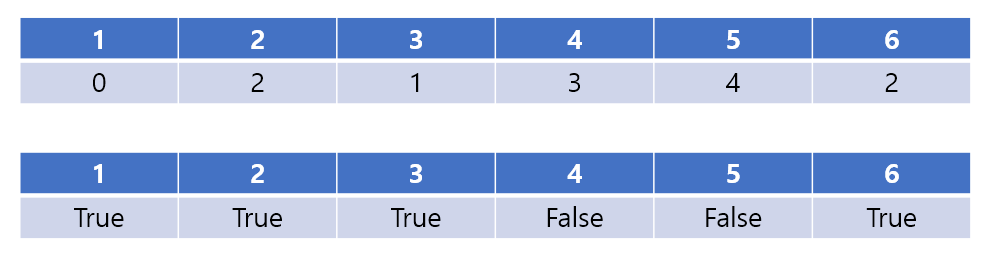
6번까지 방문했을 때의 정보는 위 표와 같다.

다음은, 4를 방문한다.
마찬가지로 갱신 사항이 없다. 아무래도 그림을 단단히 잘못 그렸다.

마지막으로 5를 방문해서 끝이 난다.

1에서 출발하여, 각 정점까지의 최단 거리는 위와 같다.

파이썬 코드

import sys

input = sys.stdin.readline
v, e = map(int, input().split())
INF = 9999999
visited = [False] * (v+1)
dist = [INF] * (v+1) # 시작노드에서부터 v로 가는 최소 비용
graph = [[] for _ in range(v+1)] # [v1에서][v2, v2로 가는 비용]

for _ in range(e) :
    v1, v2, cost = map(int, input().split())
    graph[v1].append((v2, cost))

def find_smallest() :
    min_val = INF
    min_idx = 0
    for i in range(1, v+1) :
        if not visited[i] and dist[i] < min_val:
            min_value = dist[i]
            min_idx = i
    return min_idx
    

def dijkstra(start):
    dist[start] = 0
    visited[start] = True
    # 시작노드의 인접한 노드들에 대해 최단거리 계산
    for i in graph[start] :
        dist[i[0]] = i[1]

    for _ in range(v-1) :
        now = find_smallest() # 최단거리 노드 찾기
        visited[now] = True
        # 해당 노드와 인접한 노드들 간의 거리 계산
        for next in graph[now]:
            new_cost = dist[now] + next[1]
            if new_cost < dist[next[0]] :
                dist[next[0]] = new_cost
    

dijkstra(1)

for i in range(1, v+1) :
    if dist[i] == INF :
        print("INF")
    else :
        print(dist[i])

해당 코드의 경우 시간 복잡도는 O(V^2)이다.
시작 노드를 제외하고 v-1개의 노드에 대하여 각 노드의 최소거리를 찾을 때 또 모든 노드를 탐색하기 때문이다.

시간 복잡도 문제가 생길 것인데, 각 노드의 최단거리 정보를 갱신하는 과정을 heapq 자료구조를 활용하여 O(logV) 로 줄일 수 있다. 개선된 코드는 다음 글에서 다루도록 하겠다.

여담

아... 이게 원래 갱신이 팍팍 돼야 하는데... 그래프랑 간선 정보를 무지성으로 그리다보니 갱신이 안된다... 망함