머신러닝-3단계(로지스틱회귀-분류유형(only) )

1. 로지스틱회귀 개념

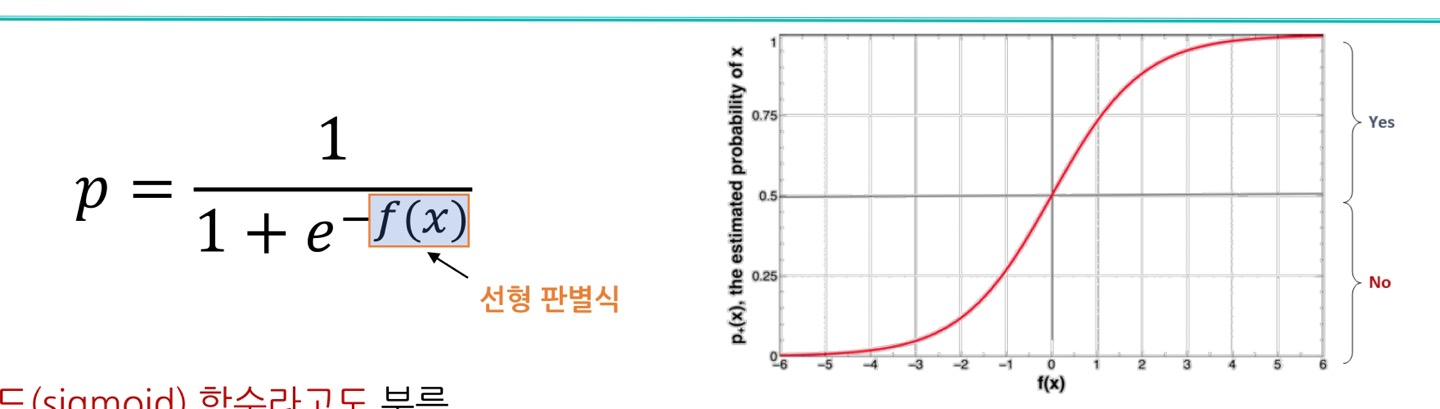
• 1) 시그모이드 함수라고도 불름

---

• 2) 0과 1범위의 확률 값을 얻는다.

---

• 3) 기본적으로 0.5를 임계값으로 하여 이보다 크면 1, 아니면 0으로 분류한다.

---

• 4) 분류 유형에서만 사용한다.

---

• 5) p = 1/(1+e^(-f(x))으로 표현한다.
  

---

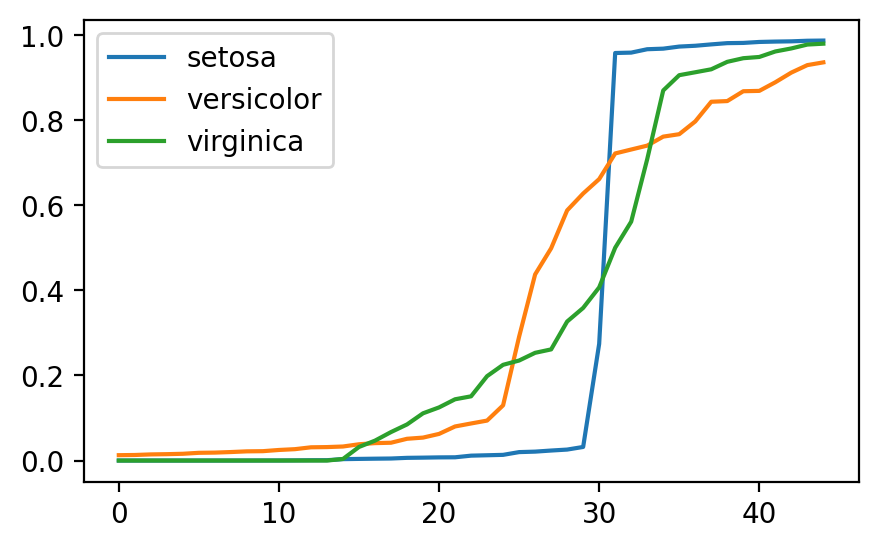
-6) model.predict_proba(x_test)를 통해 확률값을 확인하고 시그모이드 함수를 시각화해야한다.

ex)

• 분류 유형의 문제들의 풀이 순서와 동일하다.
• 차이점으로는 확률의 값을 가진다는 점이다.

# 모델링 단계 이후
----------------------------------------
# 확률값
p = model.predict_proba(x_test)
p[:10].round(2)
<출력>
array([[0.98, 0.02, 0.  ],
       [0.27, 0.72, 0.  ],
       [0.01, 0.87, 0.12],
       [0.99, 0.01, 0.  ],
       [0.  , 0.02, 0.98],
       [0.  , 0.59, 0.41],
       [0.  , 0.13, 0.87],
       [0.96, 0.04, 0.  ],
       [0.97, 0.03, 0.  ],
       [0.  , 0.03, 0.97]])
      
---------------------------------------------       

# 시그모이드 그래프 시각화

plt.plot(np.sort(p[:,0]), label = 'setosa')
plt.plot(np.sort(p[:,1]), label = 'versicolor')
plt.plot(np.sort(p[:,2]),label = 'virginica')
<출력>