[Linear Algebra] Determinants

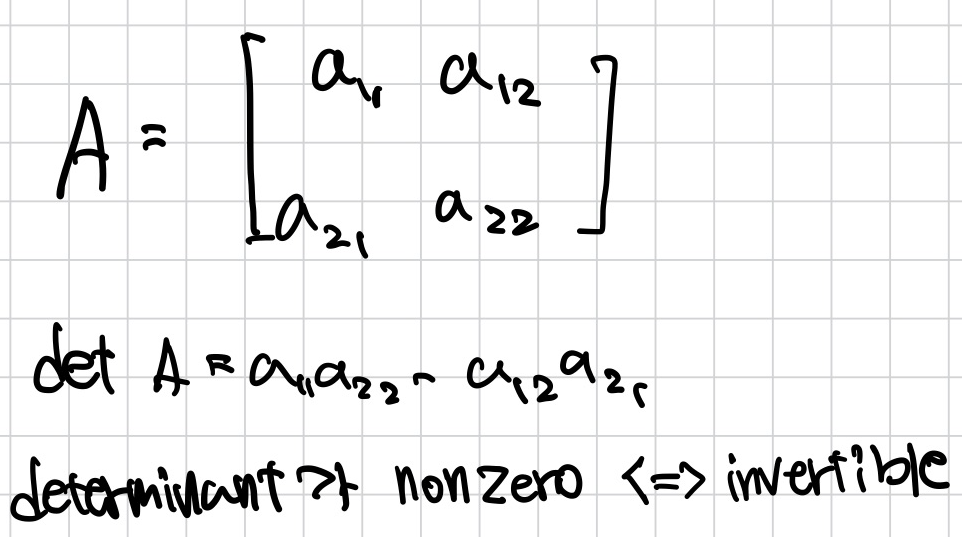
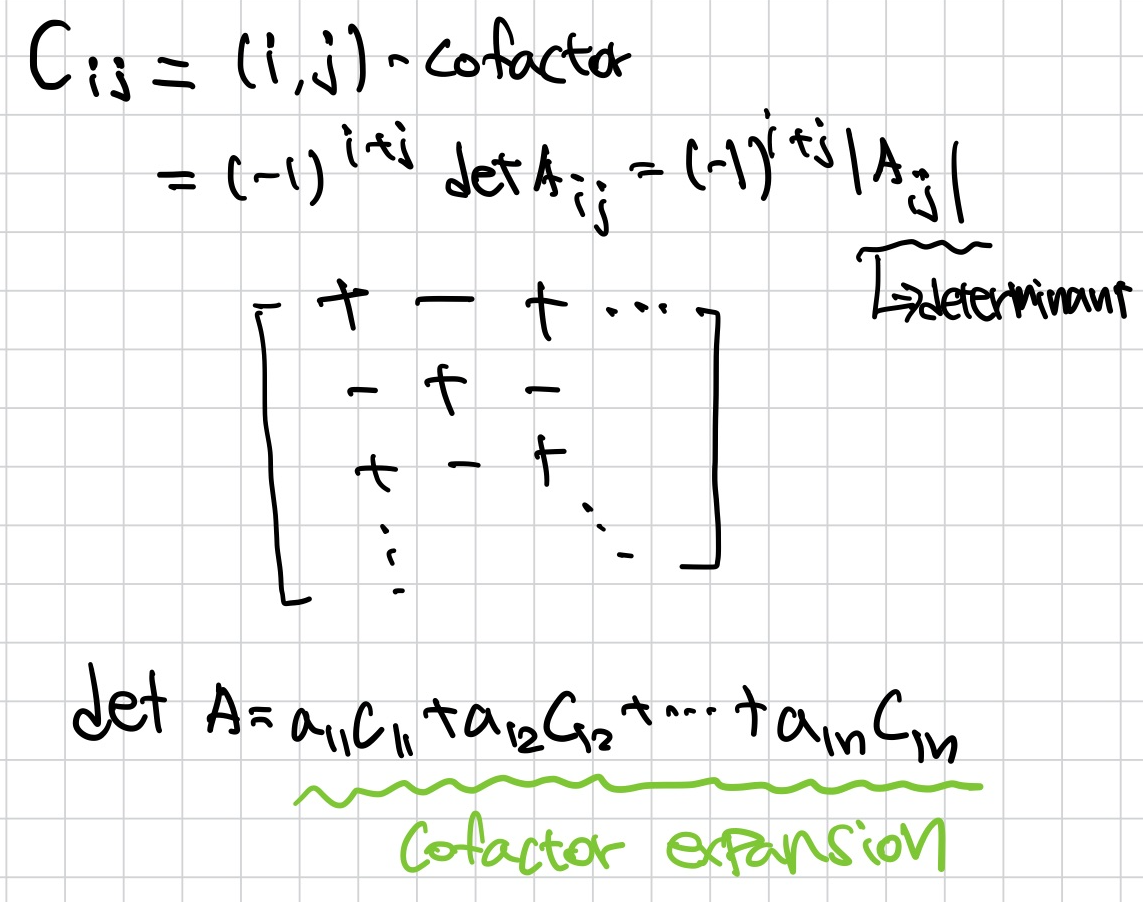
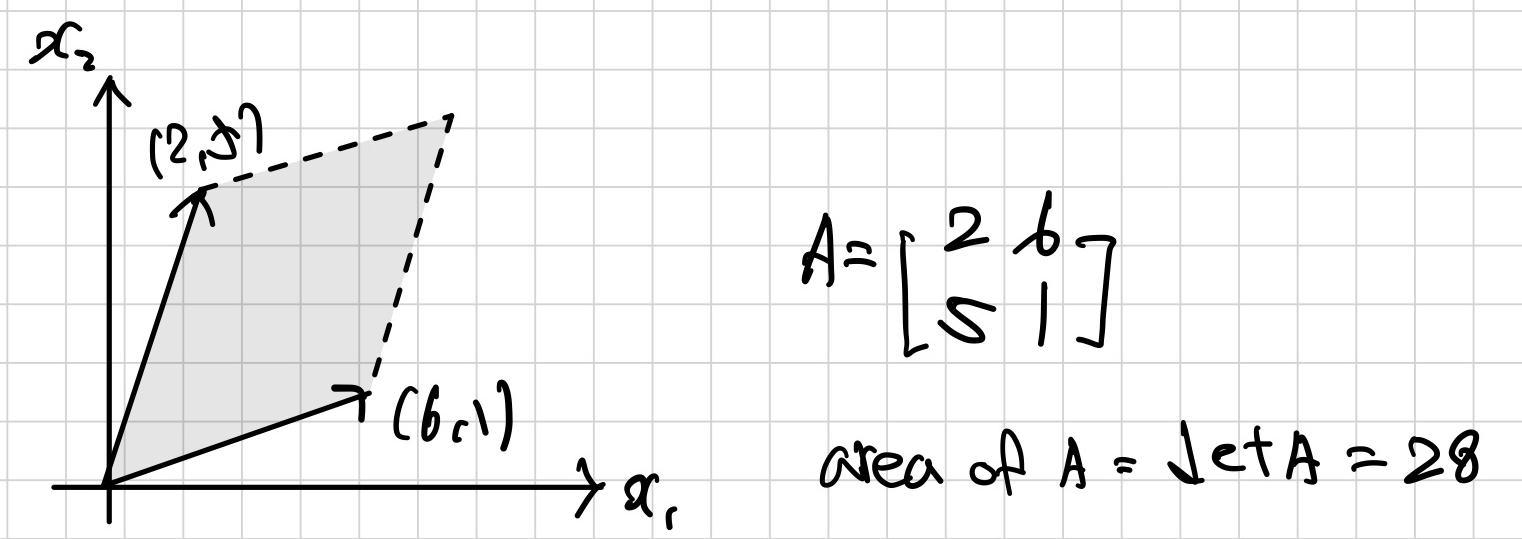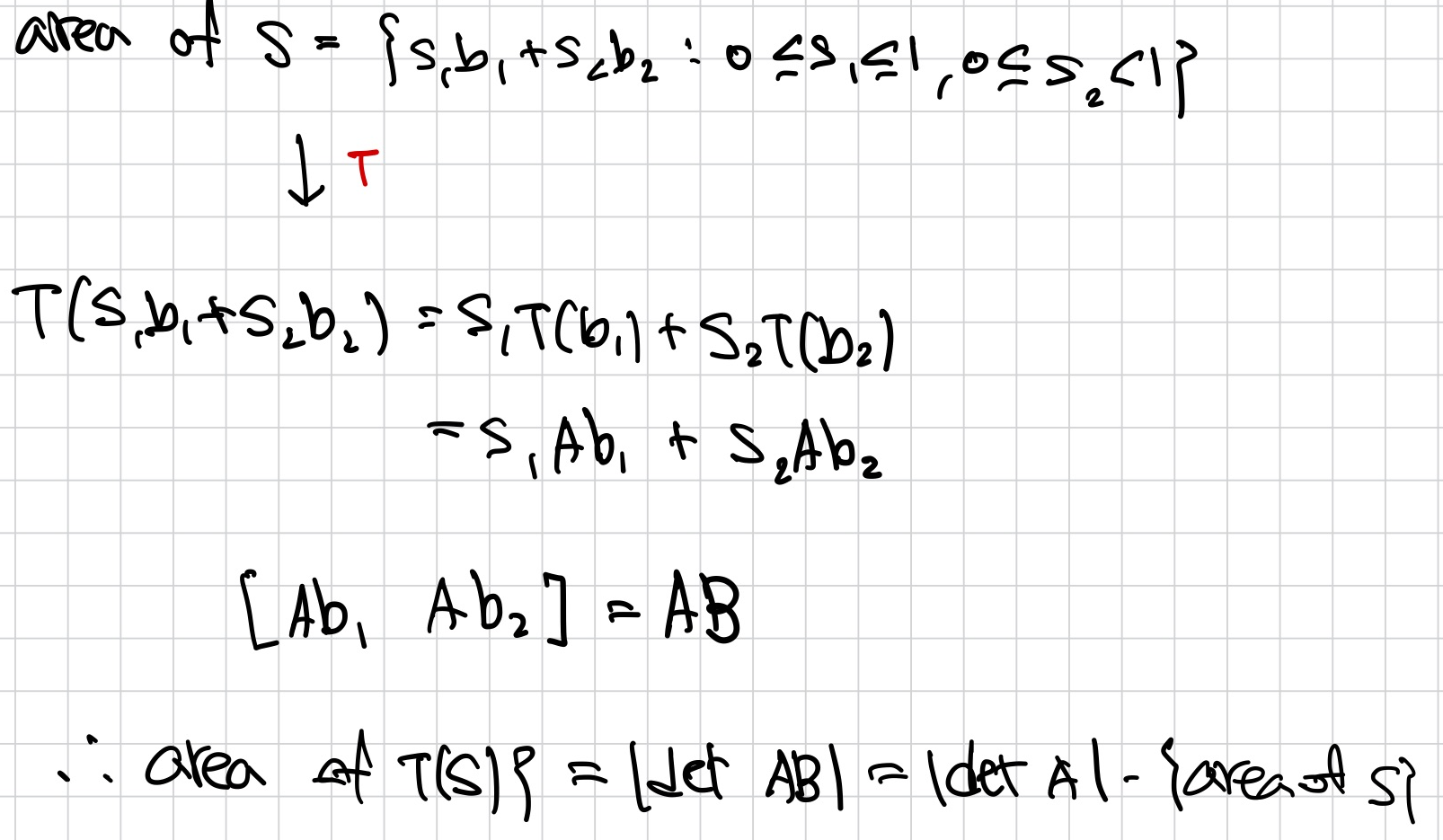• 2 x 2 matrix에서 determinant
  

Determinant

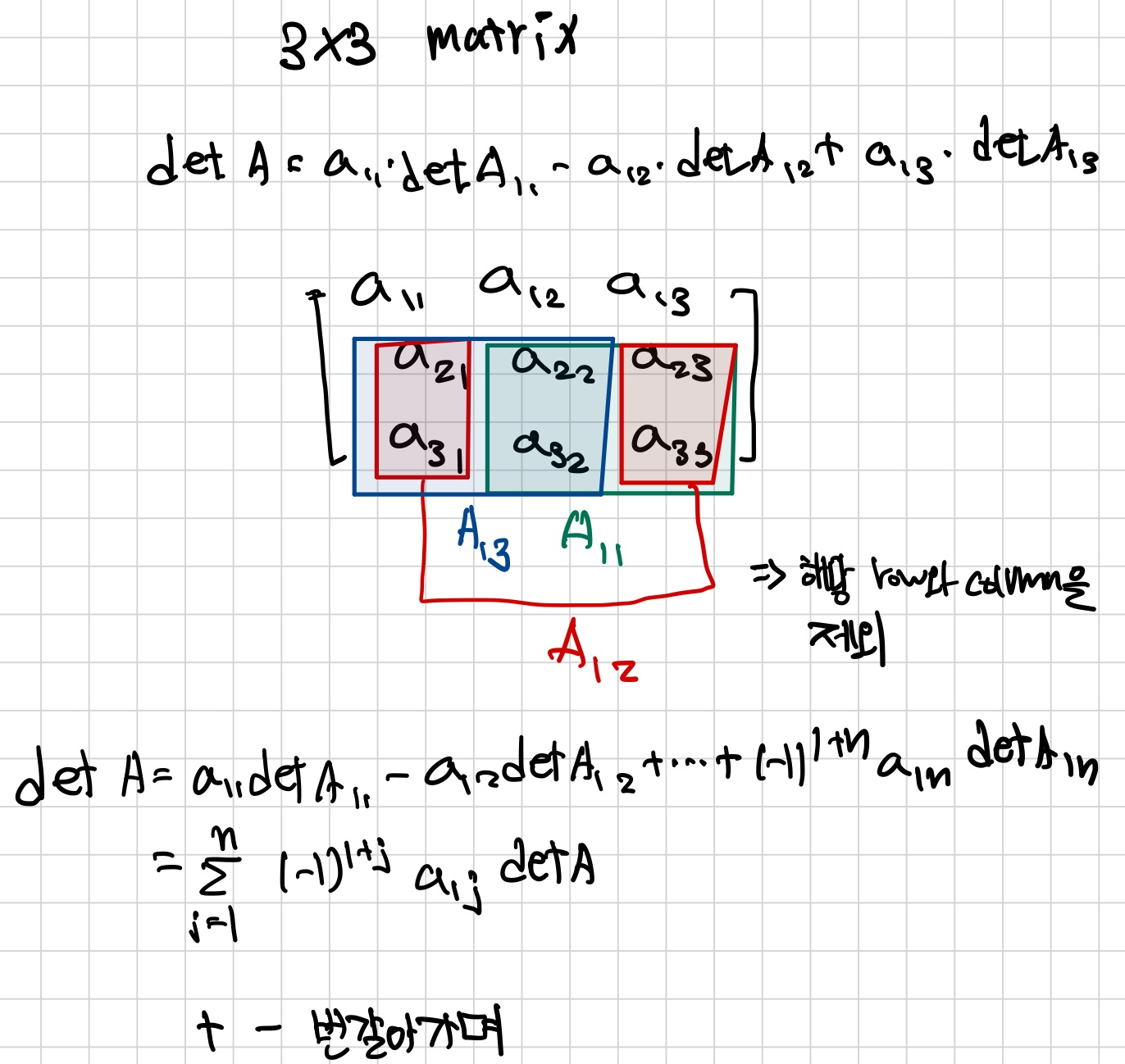
Cofactor

• 3번째 row에서 cofactor expansion을 사용하여 determinant 계산
  

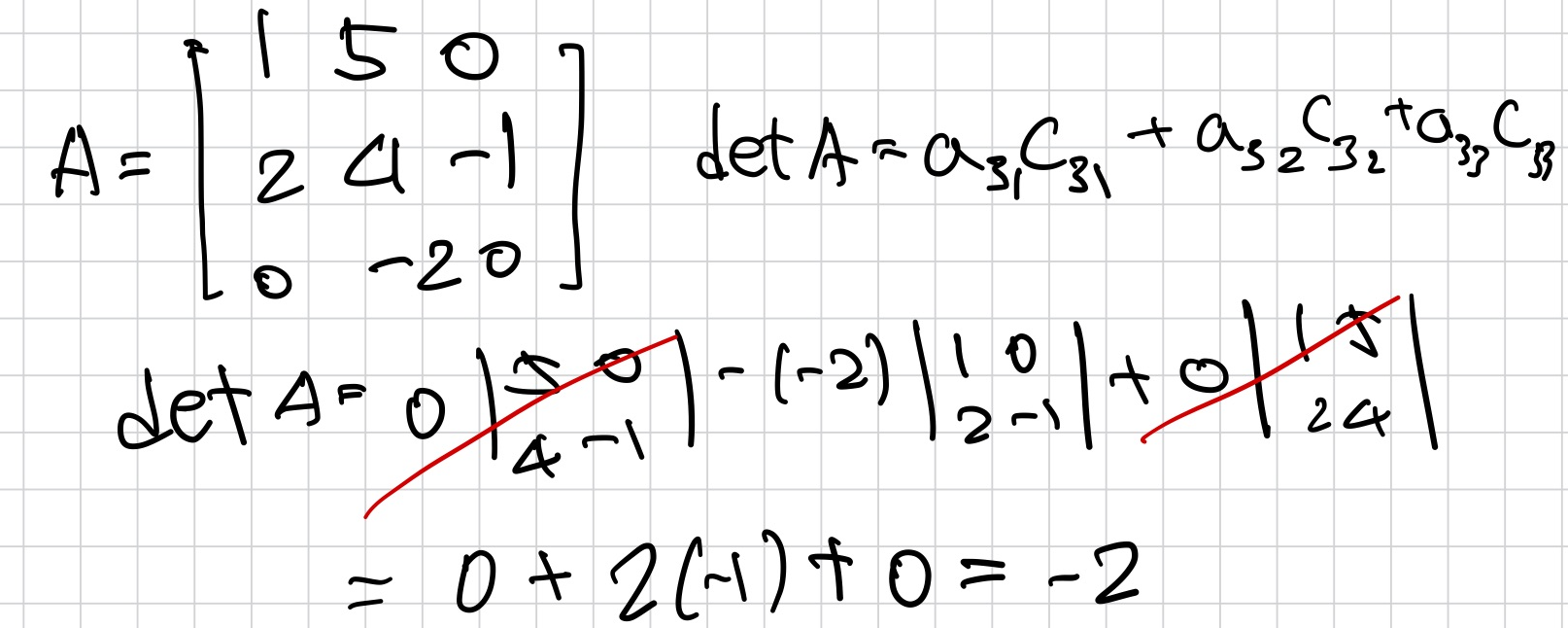
• Theorem.
  matrix A가 triangular matrix이면, det A는 A의 diagonal의 곱이다.

det EA

Theorem

• square matrix A는 invertible과 det A ≠ 0
• square matrix A는 det AT = det A이다.
• square matrix A와 B는 det AB = (detA)(det B) 하지만, 일반적으로 det A+B ≠ det A + det B이다.

A가 invertible이면, det AB를 element matrix의 곱으로도 나타낼 수 있다.

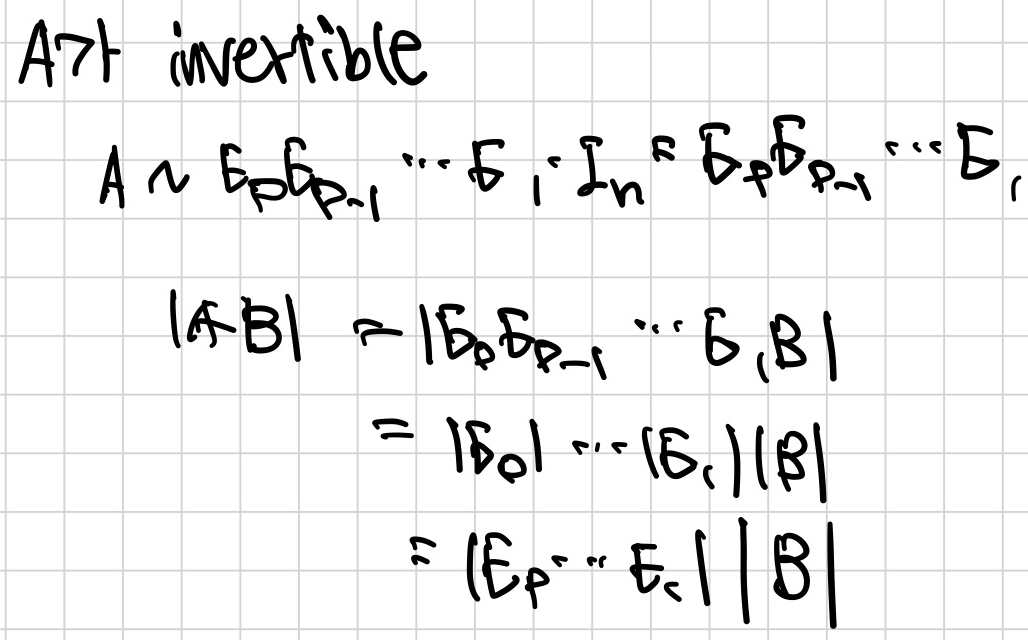
Cramer's Rule

예시 문제

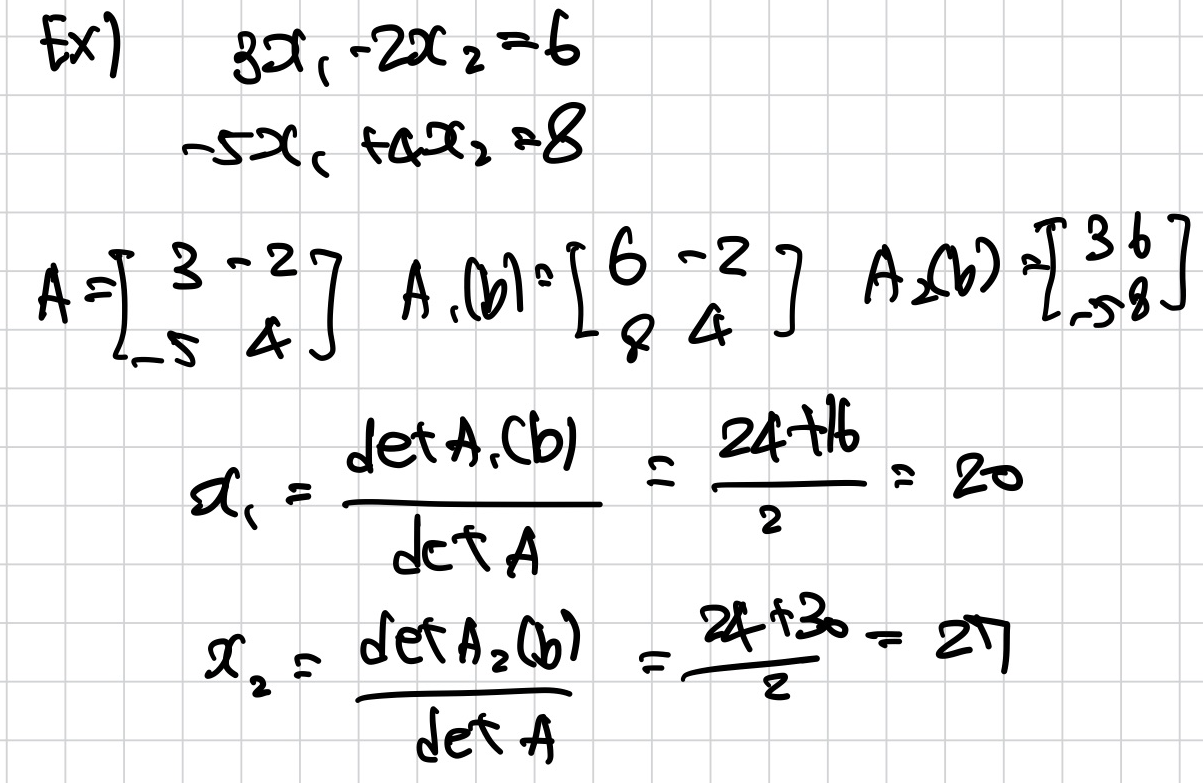
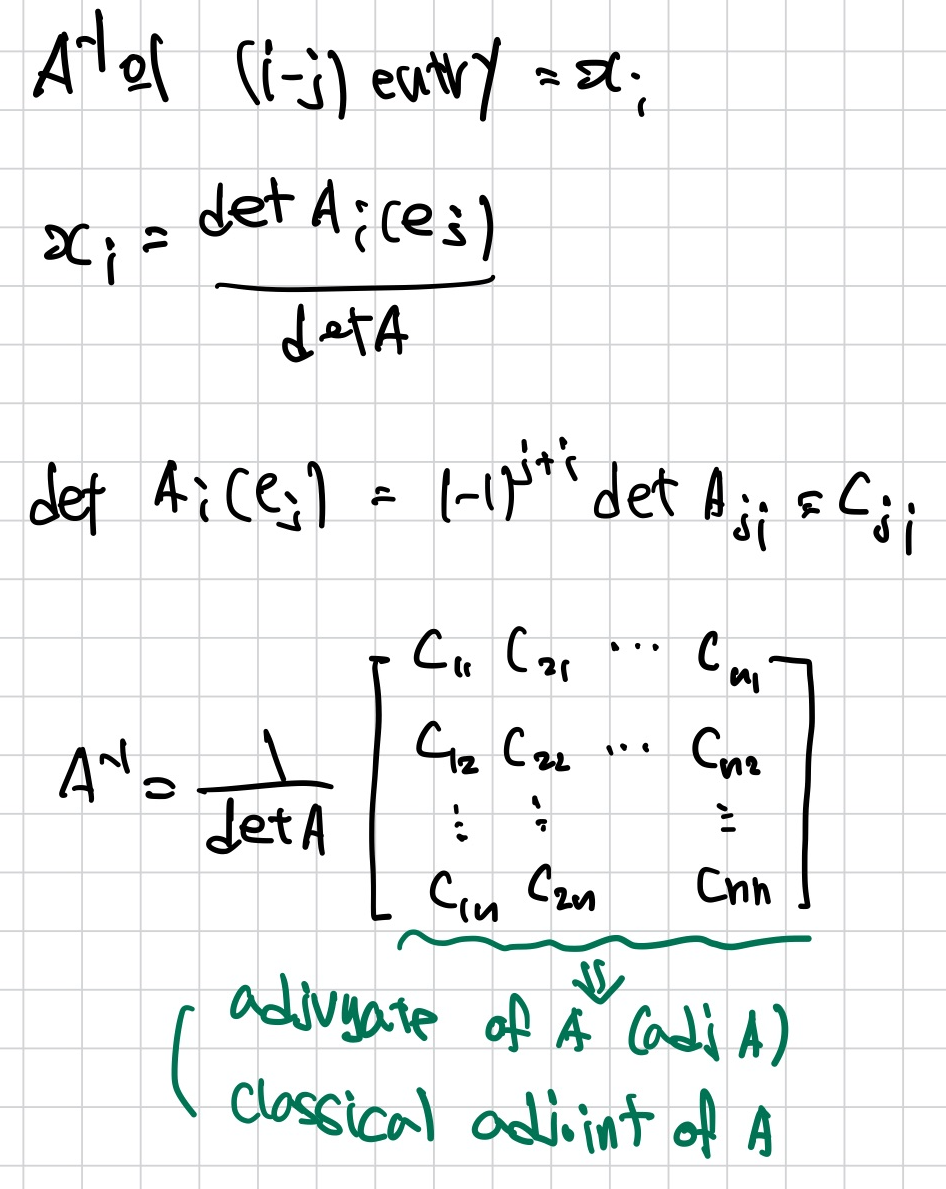
A Formula for A-1 using Cramer's Rule

Determinant로 크기(area), 부피(volume) 구하기

2 x 2 matrix A가 있을 때

• 평행사변형의 크기는 |det A|이다.
• 평행육면체의 부피는 |det A|이다.
  → row reduction을 통해 echelon form으로 변환하면 평행사변형을 직사각형 형태로 변환가능, 따라서 pivot의 곱은 원형과 동일하기 때문에 deteminant로 크기를 구할 수 있음
  

Linear Transformation

T : R2 → R2이 matrix A에 linear transformation일 때,
평행사변형 S의 크기 = |det A|·{area of S}

3 x 3 matrix A일 때,
평행육면체 V의 부피 = {volume of T(V)} = |det A|·{volume of V}