[Linear Algebra] Dimension & Rank

Coordinates and Coordinate Vector

subspace H에 basis가 있을 때, basis에 linear combination으로 만들어지는 벡터 x가 있다. 이때의 weights가 x의 coordinate vector 또는 B-coordinate vector of x라고 한다.

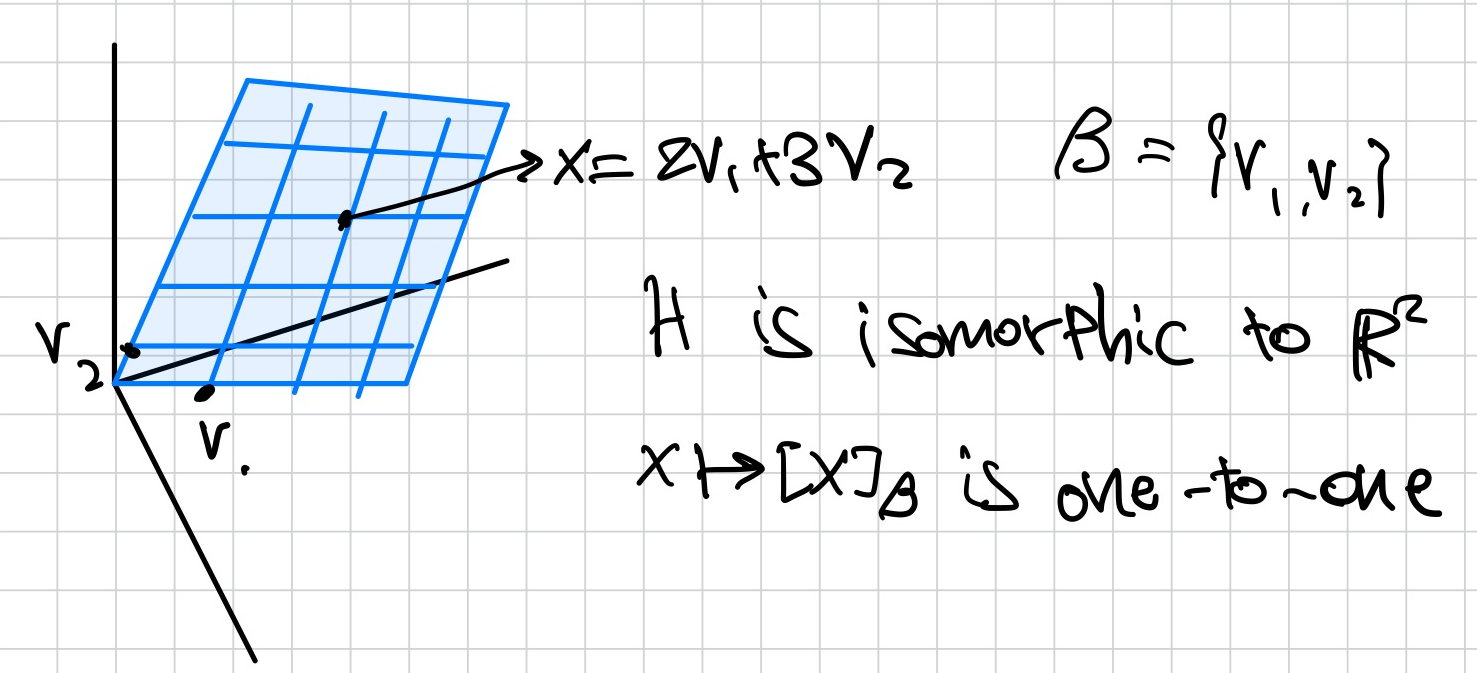
Dimension

nonzero subspace H의 dimension = dim H = H의 basis vector의 수
zero subspace {0}의 dimension = 0

• R3에서 0을 지나는 평면의 dimension = 2
• R2에서 0을 지나는 직선의 dimension = 1

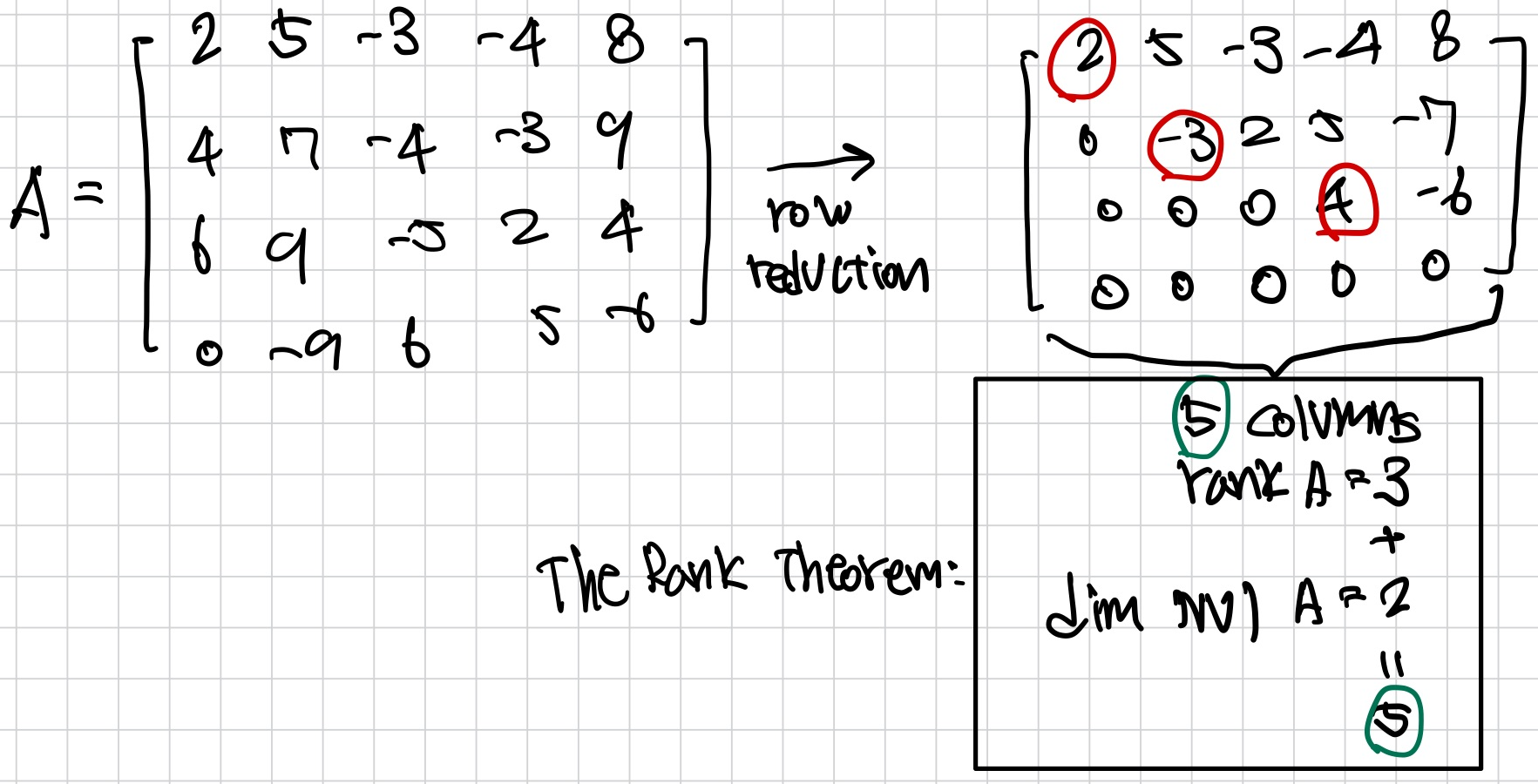
Rank

matrix A의 rank = rank A = A의 column space의 dimension

The basis Theorem

• Rn의 subspace H가 p-dimension이다.
• p개의 linearly independent set은 H의 basis이다.
• span H인 p개의 element set은 H의 basis이다.
• matrix A의 pivot의 수는 p보다 작다.

The invertible matrix Theorem

A가 n x n invertible matrix일 때,

• A의 columns은 Rn의 basis를 만든다.
• Col A = Rn
• dim Col A = n
• rank A = n
• dim Nul A = 0
• Nul A = {0} (trivial solution)

R3에 4-dimension인 subspace는 존재할까?
→ R3에서 4개의 independent한 set이 있을 수 없다.