[Linear Algebra] Diagonalization of Symmetric Matrix

Symmetric matrix

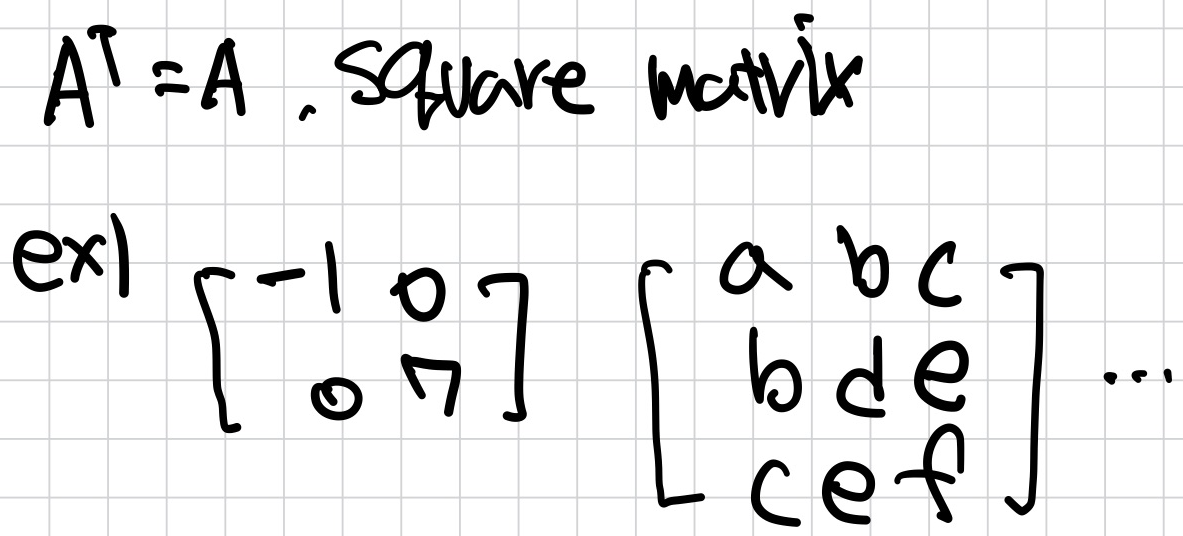
Diagonalization

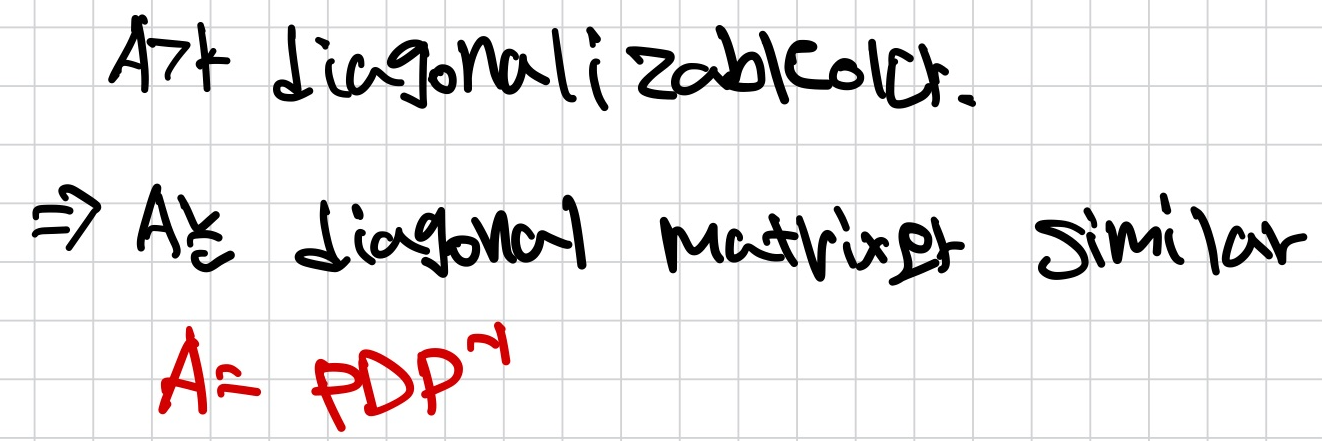
example

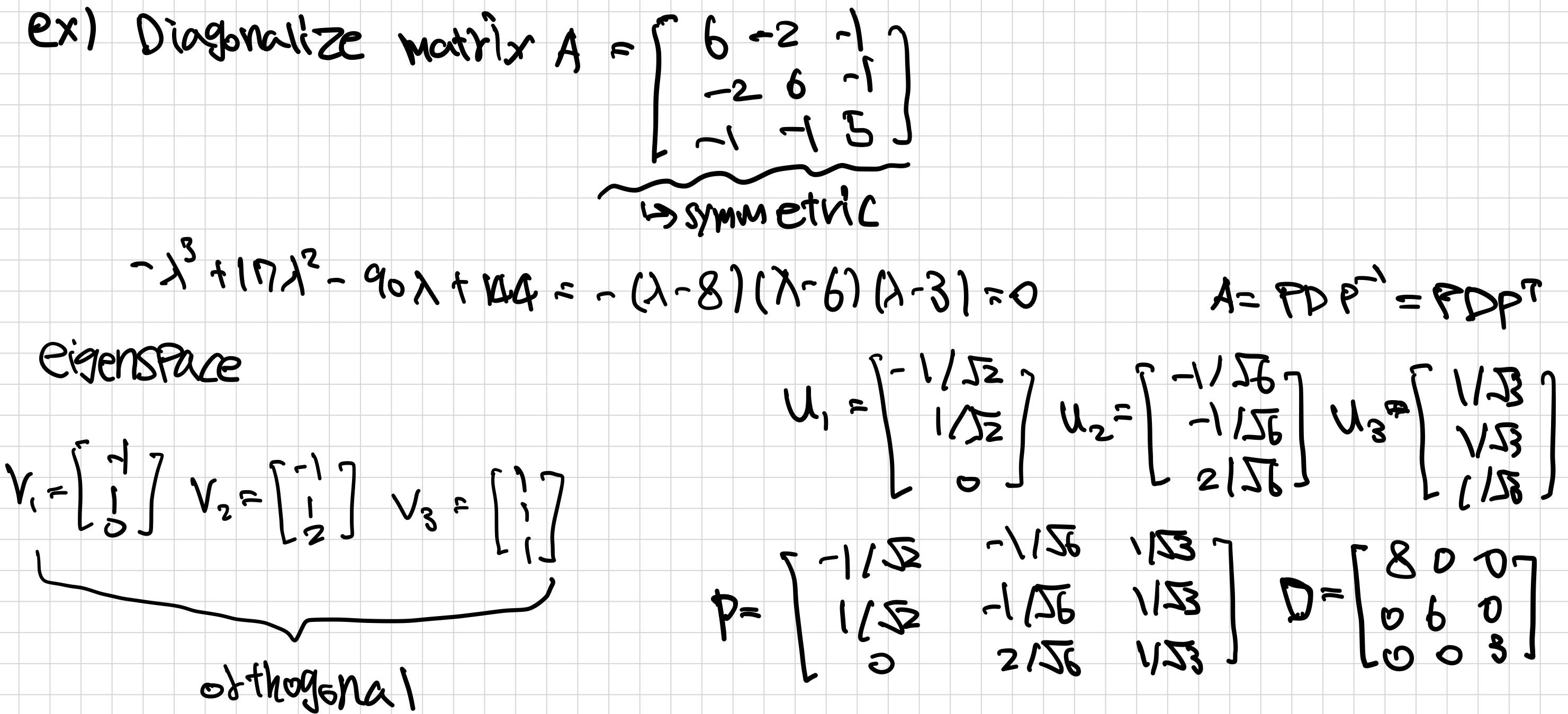
Theorem(symmetric matrix의 성질)

• 두 eigenvalue와 각각의 eigenvector
  

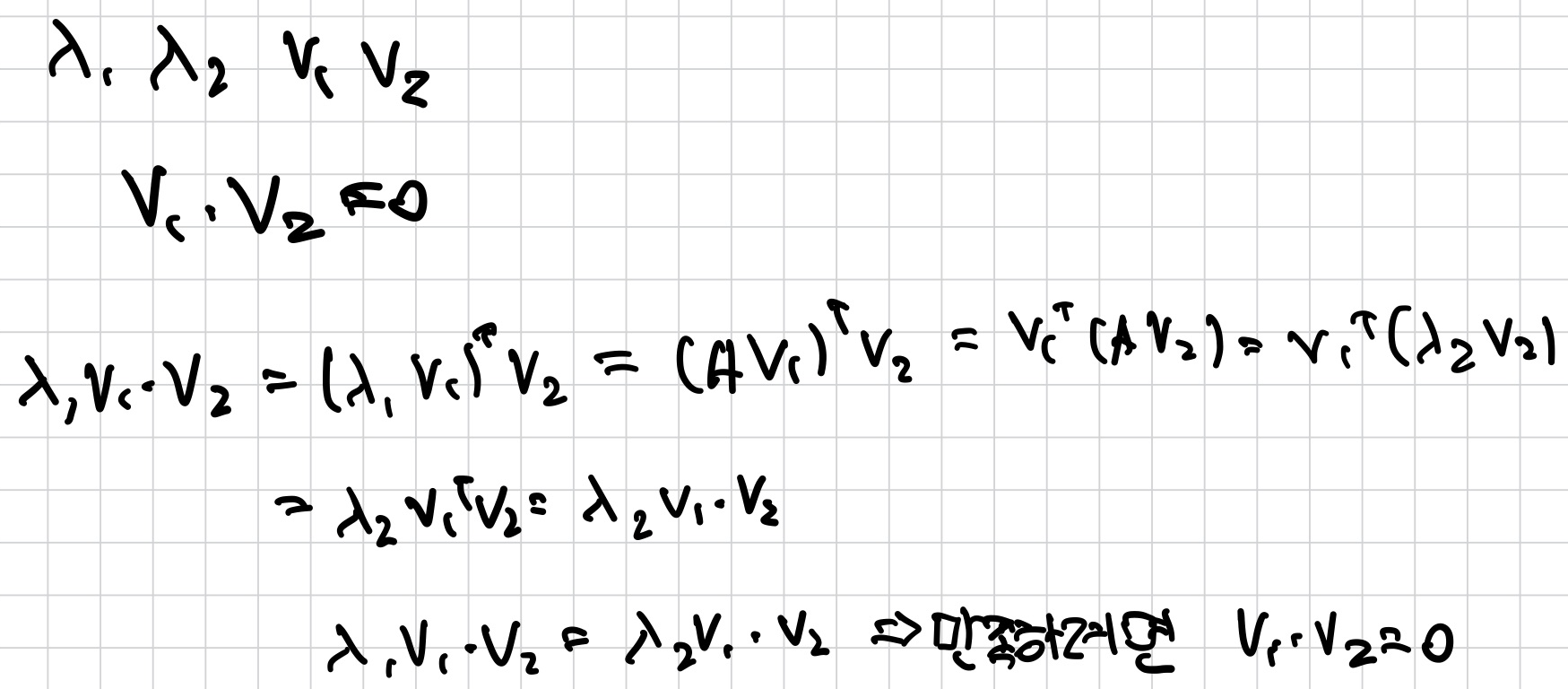
Orthogonally Diagonalizable

process

1. Check if AT = A => symmetric matrix
2. 각 eigenvalue에 대한 eigenspace를 계산
3. Gram-Schmidt process를 통해 각 eigenspace에 대한 orthogonal basis를 찾는다.
4. normalization을 통해 orthonormal basis를 구한다.
5. P, D 구하기

Theorem. The Spectral Theorem for Symmetric Matrices

n x n symmetric matrix A의 성질 :
a. A는 n개의 실수 eigenvalue를 갖는다. (중복가능)
b. 각 eigenvalue에 대한 eigenspace의 dimension은 해당 eigenvalue의 multiplicity와 같다.
c. 다른 eigenvalue에 해당하는 eigenvectors는 orthogonal이다.
d. A는 orthogonally diagonalizable이다.

Spectral Decomposition

A가 orthogonally diagonalizable이다.

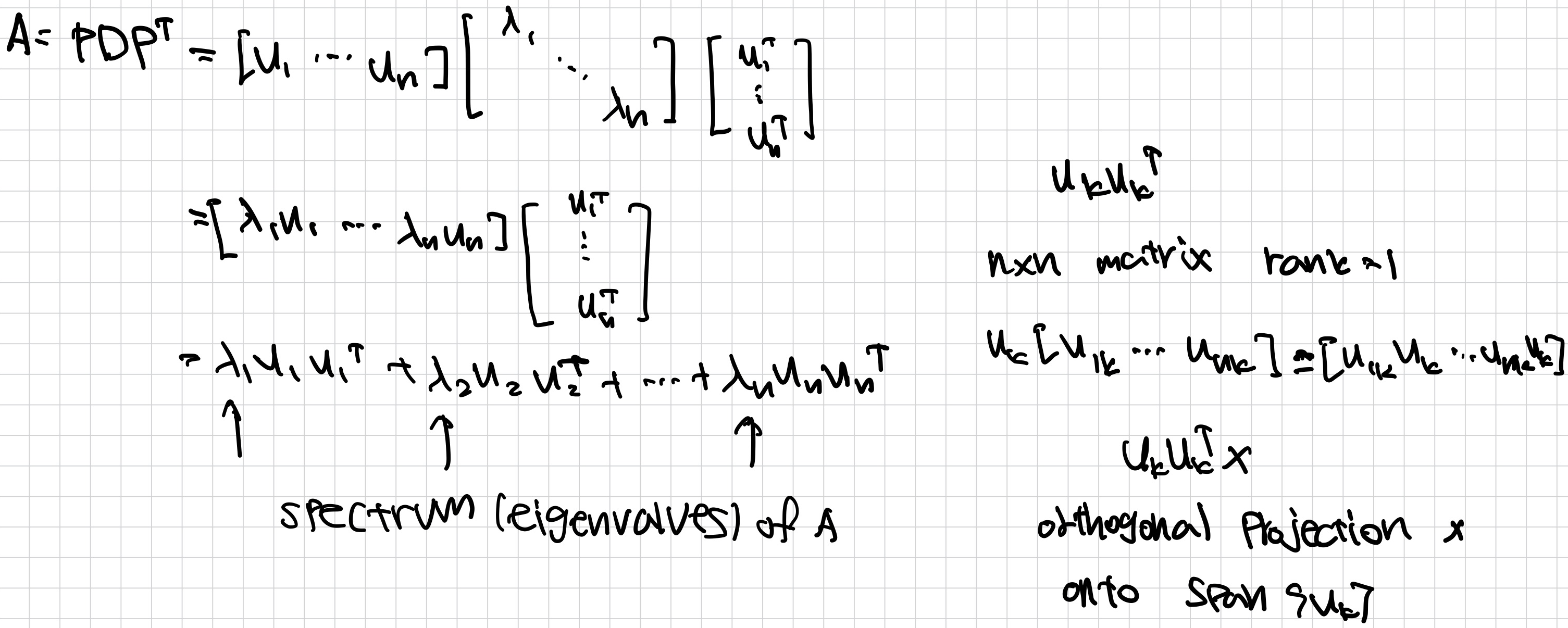
그 외 symmetric matrix의 성질(유도)

1. A가 symmetric matrix이면 A2가 symmetric이다.
   
2. A가 orthogonally diagonalizable이면 A2도 그렇다.

• A가 symmetric
• A2가 symmetric