[Linear Algebra] Type of Solution Set

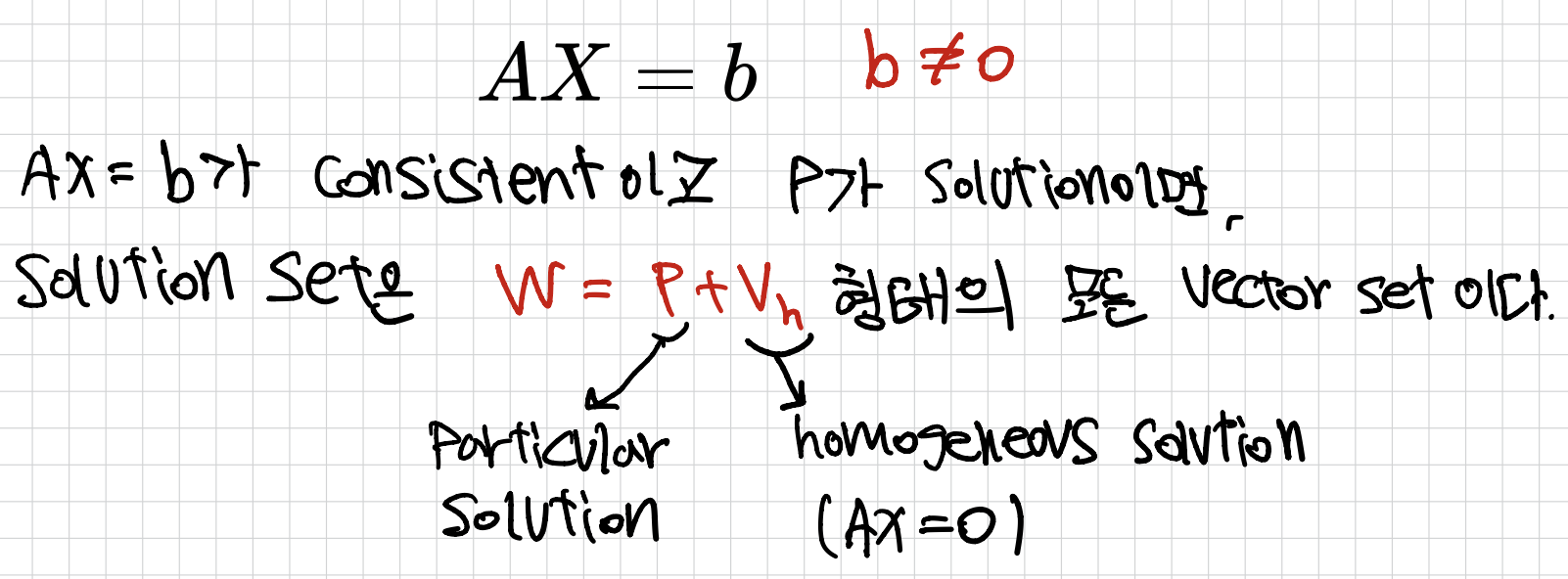
Linear Systems에서 solution 유형

• 해가 없는 경우
• 유일한 해를 갖는 경우
• 해가 무수히 많은 경우

• 해가 없다 → inconsistent(모순이 있다.)
• 해가 있다 → consistent

Homogeneous(동차) Linear Systems

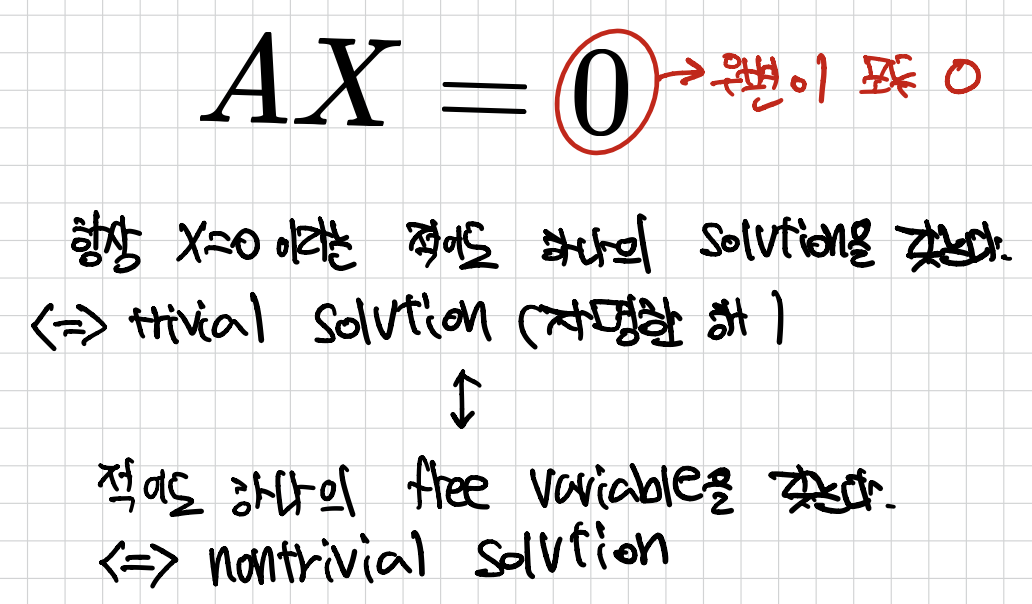
Homogeneous linear system은 X=0이라는 trivial solution을 갖는다.

• 예제
  
  
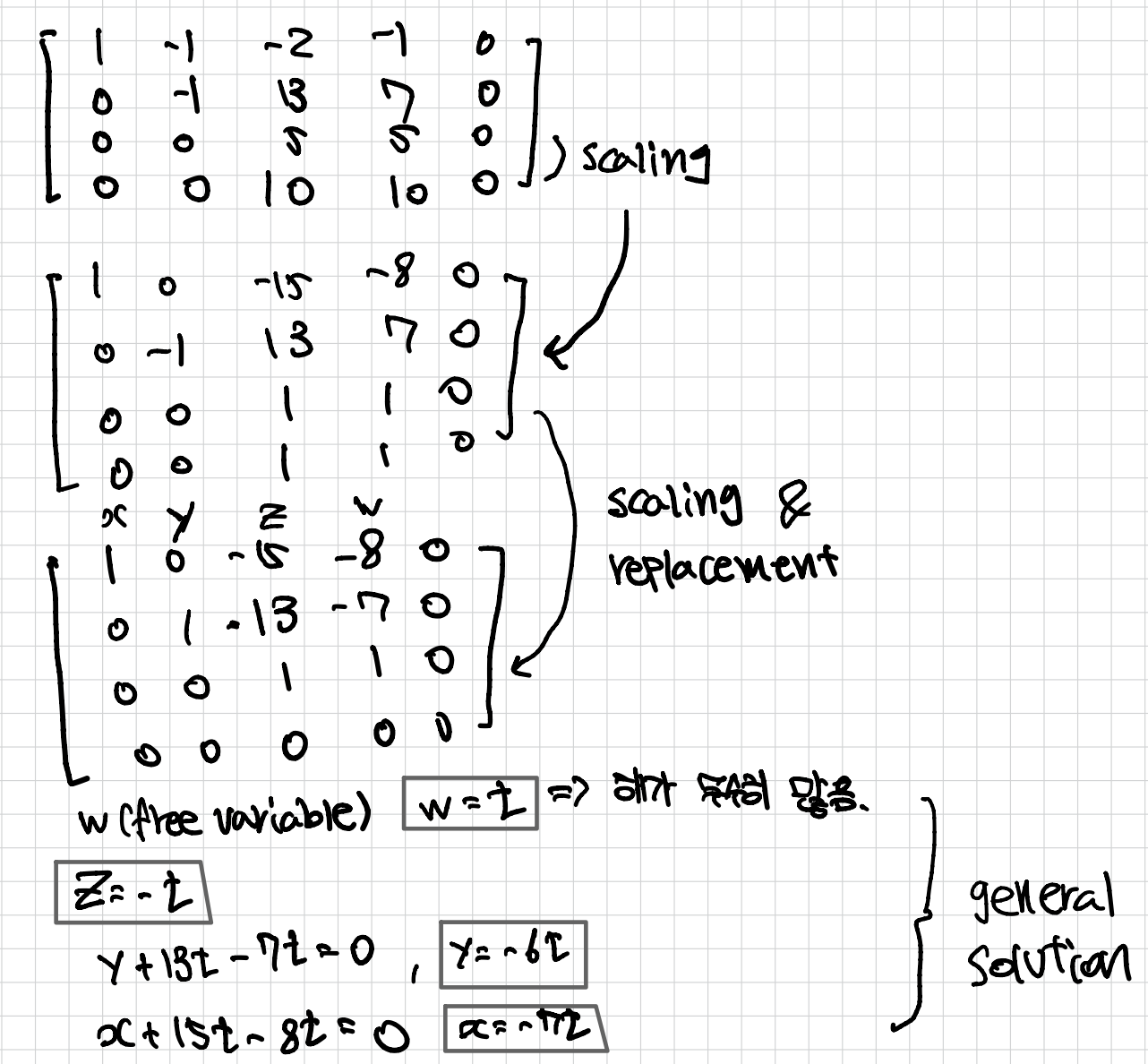
  ✔︎ t : 매개변수(parameter)
  ✔︎ 특수해(particular solution) : t에 특정값을 대입하여 나타내는 solution
  ✔︎ x=y=z=w=0
  
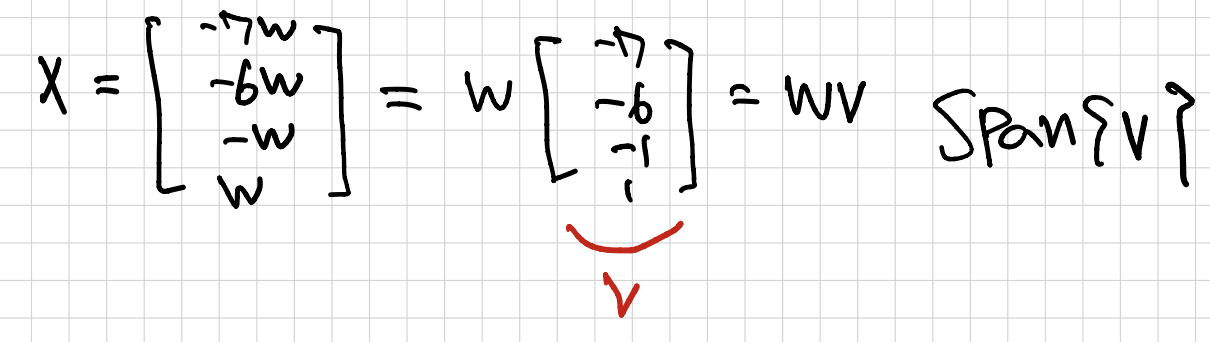
  ✔︎ 벡터 v를 span한다.

Theorem

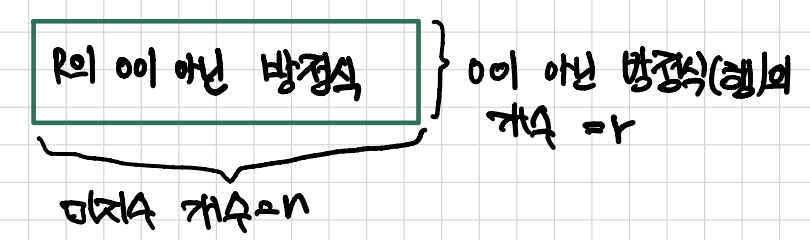
기약행 사다리꼴 R에 미지수 n개, 영행이 아닌 행 r개일 때 r<n 이면, 해가 무수히 많다.

Nonhomogeneous(비동차) Linear Systems