[CGs] Clipping Polygons

💻 Polygon Clipping

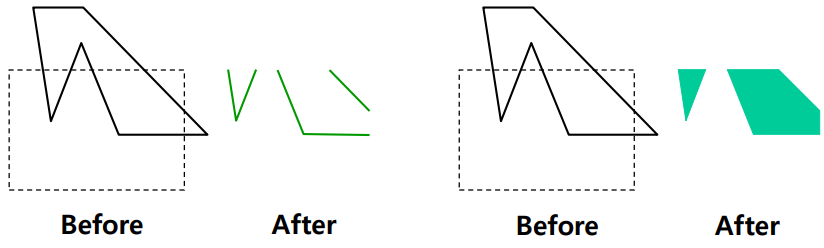
1. Line clipping으로 가공한 polygon display
2. 알맞게 clipped된 polygon display

• Polygon(다각형)은 선분들의 폐루프(closed loop)로 이루어져 있으므로 기본적으로 선분 클리핑 방법에 기반한다
• 다만 다각형의 클리핑 결과도 다각형이 되어야 하므로 단순히 선분 클리핑 이외에 추가적으로 고려해야 할 사항이 있다(Weiler-Atherton Polygon Clipping)

Examples of Polygon Clipping

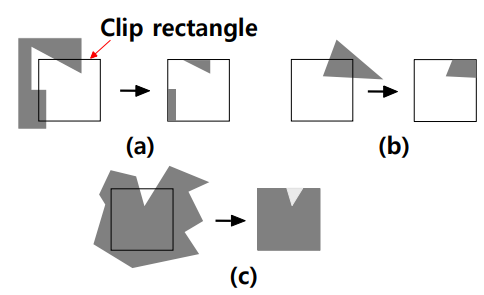
(a) Multiple components
(b) Simple convex case
(c) Concave case with many exterior edges

Sutherland-Hodgman Algorithm

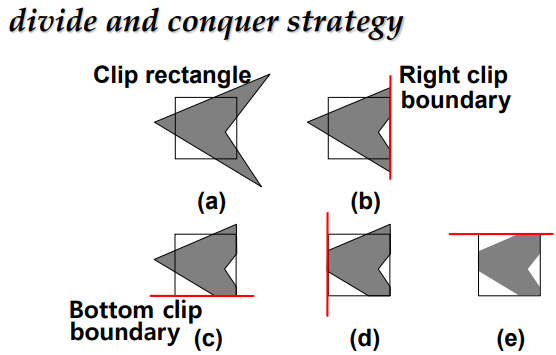
• 분할정복법 : 오른쪽, 아래, 왼쪽, 위 순서로 clipping
  • boundary 별로 분할해 clipping

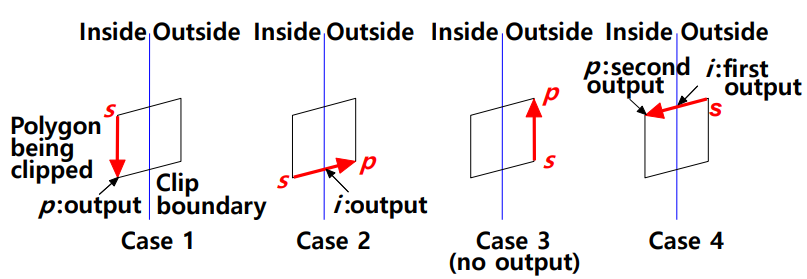
• 4가지 경우의 polygon clipping
  • Polygon을 구성하는 각 꼭지점을 저장
  • 내부에서 내부, 내부에서 외부, 외부에서 외부, 외부에서 내부 총 4가지
  • 첫 꼭짓점부터 clipping수행
  • 마지막 꼭짓점과 첫 꼭짓점을 이어 Polygon 생성
• case 1 (내부에서 내부) : 시작점과 끝점 저장
• case 2 (내부에서 외부) : 시작점과 변이 window와 만나는 점 저장
• case 3 (외부에서 외부) : 저장 안함
• case 4 (외부에서 내부) : 변이 window와 만나는 점과 끝점 저장

• $P =$ {$V_{1}, V_{2}, V_{3}, V_{4}, V_{5}, V_{6}, V_{7}$} ---> $P =$ {$V_{3}^{'}, V_{4}, V_{4}^{'}, V_{5}^{'}, V_{6}, V_{7}, V_{7}^{'}$}
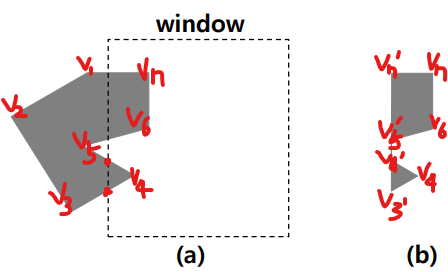
• Sutherland-Hodgman Algorithm을 쓰면 (b)그림처럼 polygon이 분할되어야 하는데 붙어있다
  • 결국 원하지 않는 결과가 나올 수 있는 이 알고리즘의 한계이다.
• Polygon의 특성상 시작점($V_{3}^{'}$)과 끝점($V_{7}^{'}$)이 연결되는데, 끝점과 시작점을 이을 때 (b)처럼 되는 문제점이 생긴다

---

Weiler-Atherton Polygon Clipping

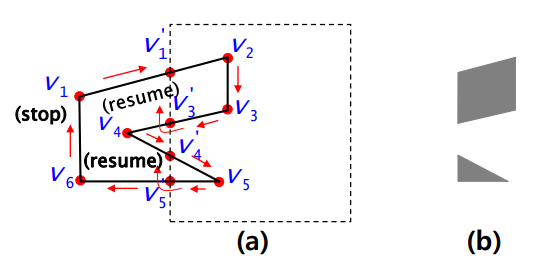
• Sutherland-Hodgman Algorithm을 사용해 분할하면, polygon이 붙어있는 문제점을 해결하기 위해 Weiler-Atherton Algorithm을 사용
• Multiple component를 생성하기 위해 내부에서 외부로 갈 때 생기는 점은 첫 꼭지점과 연결시킨다.
  • $P =$ {$V_{1}^{'}, V_{2}, V_{3}, V_{3}^{'}$}
  • $P =$ {$V_{4}^{'}, V_{5}, V_{5}^{'}$}

---

All-or-none String-Clipping

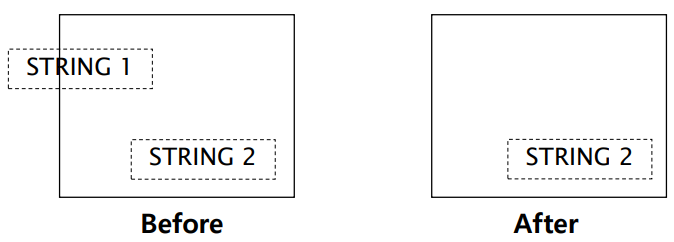
• String을 싸는 영역이 window에 걸쳐지면 전체를 버린다.
• 즉, 완전히 포함된 경우만 나타낸다.

All-or-none Character-Clipping

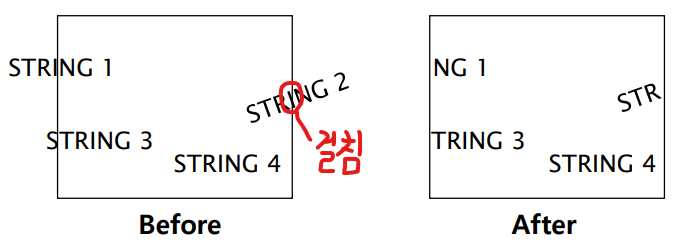
• 문자 단위로 window에 걸치는 부분은 버린다.

Clipping the Components of Individual Characters

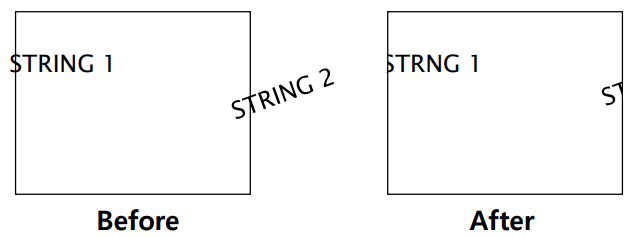
• 문자 개개 획 단위로 걸쳐지는 부분까지 표시