💻 Liang and Barsky Algorithm
Basic Idea
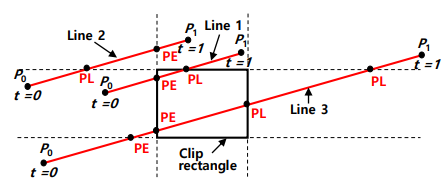
-
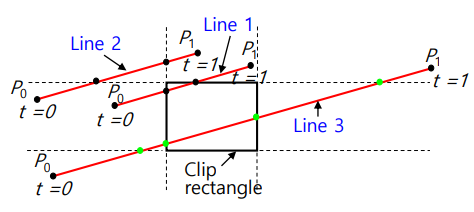
clip edge를 무한으로 늘린 선과 edge가 교차하는 부분의 점들을 대표하는 값을 찾는다.
- 선이 시작하는 점 = = 0
- 선이 끝나는 점 = =
- 0 <= <=
-
clip edge는 선에 교차하여 최대 4가지 값이 계산된다.
- and 의 경우 2개의 값
- 의 경우 4개의 값
-
4가지 값 중 실제 교차점(window의 경계선과 교차하는 점)과 허수 교차점(window의 경계선의 연장선과 교차하는 점)을 구분해야 한다
-
4가지 교차점에 대응하는 값 중 실제 교차하는 부분은 한개나 두개이다.
- 일반적으로, 이것은 Cohen-Sutherland의 교차점 계산 알고리즘에 비해 시간을 절약할 수 있는데, 이유는 많은 clip-rectangle edge를 clip하는 반복적인 작업을 피할 수 있기 때문이다
-
Liang and Barsky Algorithm은 Cyrus-Beck Algorithm을 향상시킨 것으로, 모든 4개의 값이 계산되기 이전에 필요없는 line segment를 버린다.
Parametric Representation of the Line
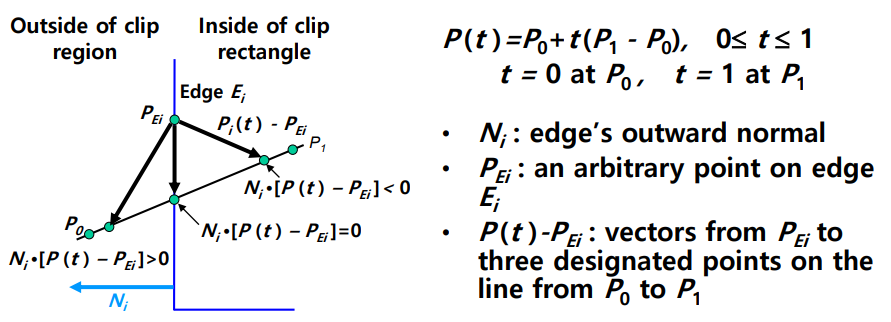
-
: edge 표면의 법선 벡터, edge에서 바깥으로 직각(90)방향으로 향해야한다.
- 왼쪽 edge일 경우 그림과 같은 형태
- 밑쪽 edge일 경우 는 아래쪽으로 향한다.
-
: edge 의 임의적인 점
-
: 점에서 점까지의 벡터, 는 에서 까지 선에 존재하는 점
Vector

내적 계산법
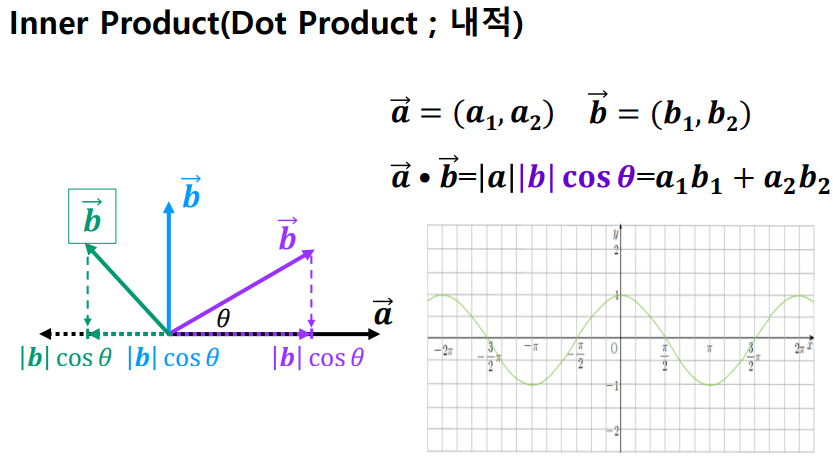 오른쪽 그래프는 의 그래프이다.
오른쪽 그래프는 의 그래프이다.
축은 이며 /2 = 이다.
-
의 머리 위에서 조명이 비추고 생긴 그림자이다.
즉, 의 그림자 길이 = -
만약 가 지면과 맞닿는다면 그림자의 길이는 의 길이와 같을 것이다.
즉, 일 때 이고 는 지면과 평행하다. -
< (예각) 이라면 이므로 > 0
-
= (직각) 이라면 이므로 = 0
-
> (둔각) 이라면 이므로 < 0

- < 0 : window의 내부
- = 0 : window의 경계선에 가 위치
- > 0 : window의 외부
How the Algorithm Works

-
나눗셈을 계산할때 오차를 조심해야하며 분모가 0이 되면 안된다.
-
값을 구할때 는 법선벡터이므로 길이가 보통 1인데 절대 0이 되어선 안된다
-
(선분의 distance : -)도 0이 되어서는 안된다.
- 의 길이가 0이라면 선분이 될 수 없다. 0이라면 선분이 아닌 점이다.
-
도 0이 되어선 안된다
- 이라면 Edge와 가 직각이다.
- 즉, Edge와 선분이 평행하다는 뜻이므로 절대 평행하면 안된다.
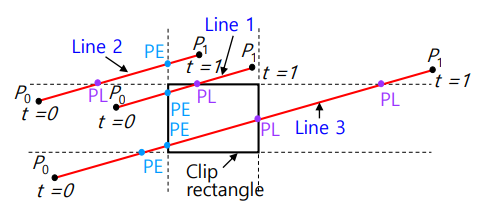
-
위의 식을 계산하여 범위를 제외한 값은 버린다.
-
Clip 경계선에 있는 교차점을 결정해야 한다
-
남은 t를 sorting하고, 교차되는 점들 중 중간 값을 선택해야 한다()
-
의 경우 중간값을 선택해도 edge에 속하는 점이 아니고, 의 경우, 중간값이 4개나 있어 어떤 점을 선택할지 결정해야 한다.
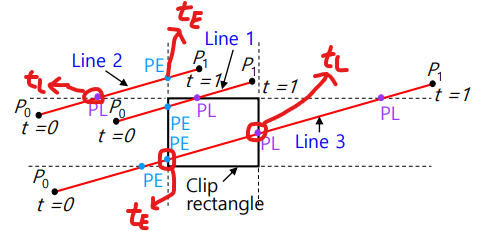
-
PE : 들어가는 교차점
- 와 가 이루는 각도가 이상인 둔각이어야한다.
-
PL : 들어가는 교차점
- 와 가 이루는 각도가 이하인 예각이어야한다.
-
두개의 교차점은 늘 반대되는 label(PL,PE)를 가진다
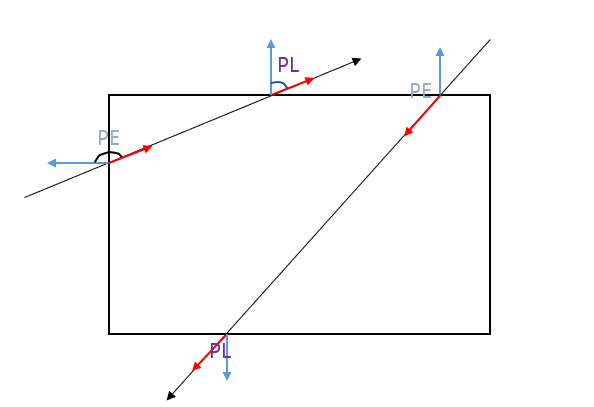
-
교차되는 선분은 range(,)로 결정된다
-
: 가장 t값이 큰 PE
-
: 가장 t값이 작은 PL
-
다각형 내의 선은 항상
- 만약 이라면, Trivial rejected상태를 의미한다.
Cohen-Sutherland Algorithm vs Parametric Algorithm
-
Cohen-Sutherland Algorithm은 구현 난이도가 쉽다(단순하다)
-
Cohen-Sutherland Algorithm은 trivially rejected된 것도 clipping대상이 되어 불필요한 연산을 해야 한다, 한번에 선을 자르는 것이 아니라 여러번 해야 한다, 사각형처럼 9개의 region에서만 사용 가능하다
-
Parametric Algorithm은 모양의 다양성이 높다
-
t값이 음수 or 1보다 큰 양수인 경우, 불필요한 계산을 해야 한다
