1-3. SVD Application

본 글은 K-MOOC의 인공지능 수학 고급(Advanced Mathematics for AI) 강의를 듣고 요약한 글입니다.

Question

1-1. Data representation 에서 봤던 데이터를 다시 가져오자.

$d_1$: Romeo and Juliet
$d_2$: Juliet O happy dagger
$d_3$: Romeo died by dagger
$d_4$: Live free or die that is the New-Hampshire's motto
$d_5$: Did you know New-Hampshire is in New-England

자, 여기에서 die와 dagger에 관련된 문서를 찾으라는 문제가 나왔다면 어떻게 접근할 수 있을까?

$d_2$, $d_3$, $d_4$은 제목에 단어들이 있다. 아마 연관성이 있을 것이다.
$d_5$는 아무 단어도 없다. 그리고 연관성도 없다.
$d_1$은 아무 단어도 없다. 하지만..? 사실 로미오와 줄리엣은 die와 dagger와 연관이 있는 소설의 제목이다.

이러한 숨은 의미를 발견할 수 있을까?

Solution: Latent Semantic Indexing

우리는 문서들에 숨은 의미를 찾아내야 한다.

1-1. Data representation 에서 만들었던 행렬을 다시 가져오자.

	romeo	juliet	happy	dagger	live	die	free	New-Hampshire
$d_1$	1	1	0	0	0	0	0	0
$d_2$	0	1	1	1	0	0	0	0
$d_3$	1	0	0	1	0	1	0	0
$d_4$	0	0	0	0	1	1	1	1
$d_5$	0	0	0	0	0	0	0	1

이 행렬을 분해하여 숨은 의미를 찾을 수 있지 않을까?

우리는 1-2. Matrix Decomposition 에서 여러 분해 기법을 살펴보았고, 해당 행렬은 정사각행렬이 아니기 때문에 마지막으로 다룬 SVD가 가능해보인다.

잠깐 SVD에 대해서 짚고 넘어가자.
주어진 행렬 $A_{M\times N}$를 $A_{M\times N} = U_{M\times M}\Sigma_{M\times N}{V_{N\times N}}^T$ 로 분해하는 것을 full SVD라고 부른다.
실제로 이와같이 full SVD를 하는 경우는 드물며 아래 그림들과 같이 reduced SVD를 하는게 일반적이다.

• thin SVD
  
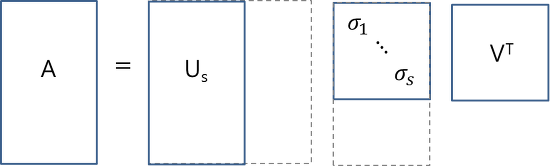
• compact SVD
  
• truncated SVD
  

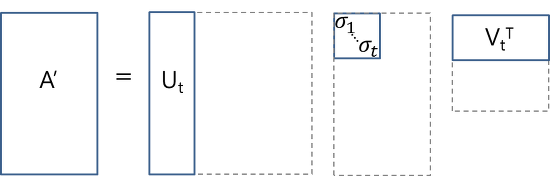
여기서 우리는 데이터들간의 유사성을 판병해야 하고 2차원 평면 위에서 쉽게 표현하기 위해 다음과 같은 reduced SVD를 적용할 것이다.

그 결과 아래와 같은 데이터들을 얻을 수 있다.

여기에서 본래의 가중치(특이값, Singular value)를 각각 $U$와 $V$에 곱해주면 각각의 문서, 단어들의 벡터를 구해줄 수 있다.
(Document vector: $U\Sigma$, Word vector: $\Sigma V^T$)

자 이제 쿼리의 벡터를 구해주기 위해 die 벡터와 dagger 벡터의 평균을 내주자.

마지막으로 문서들과 쿼리 벡터를 2차원 평면위에 나타내어 보자.

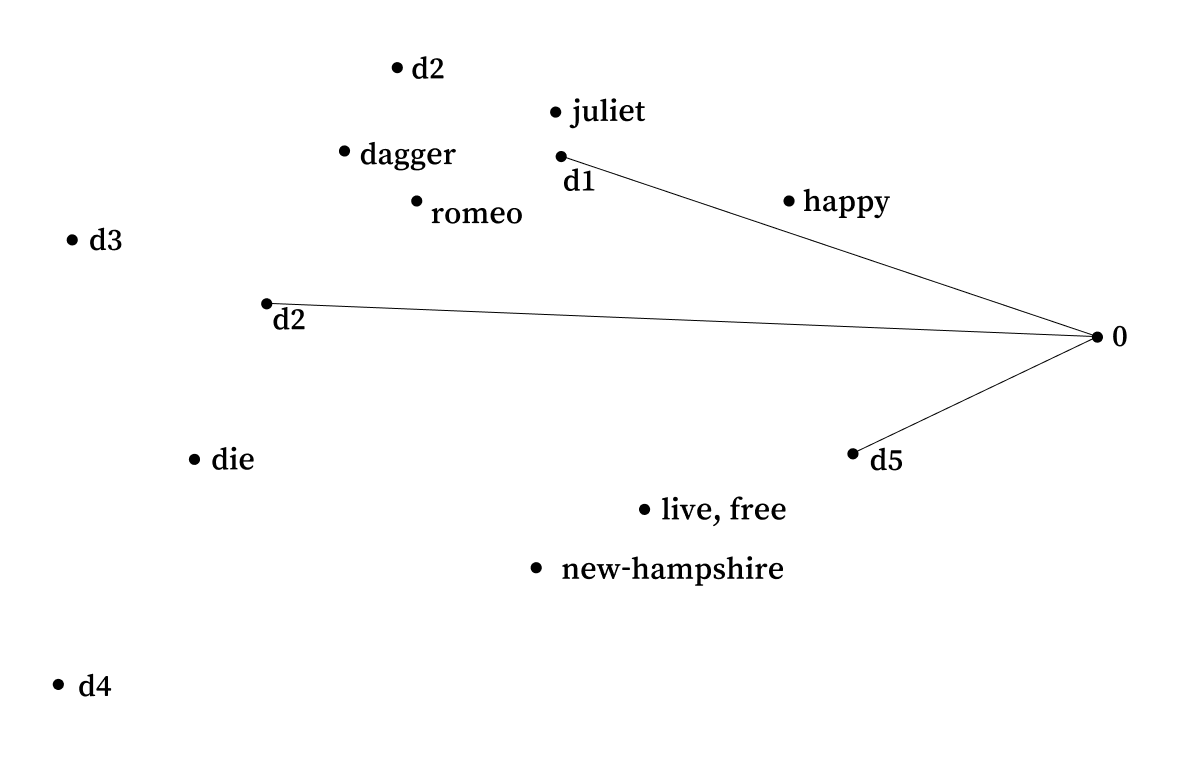
그 결과 겉으로는 둘 다 아무 단어도 포함되어 있지 않은 $d_1$과 $d_5$였지만, 현재는 $d_1$이 더 좁은 각도를 나타내는 것을 볼 수 있다.

이런 식의 분석법을 Latent Semantic Indexing이라고 한다.