2-5. Convex Optimization

본 글은 K-MOOC의 인공지능 수학 고급(Advanced Mathematics for AI) 강의를 듣고 요약한 글입니다.

Convex Function

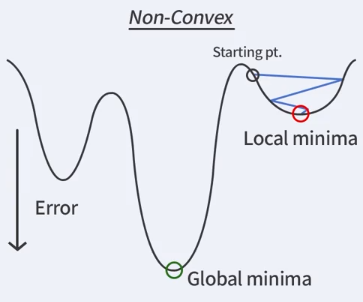
만약 Convex Function이 아니라면 위와 같이 Local minimum에 도달할 수 있다.

하지만 Convex Function이라면 Global minimum에 도달한다는 것이 보장된다.

Properties

음이 아닌 계수들만으로 이루어진 Convex Function들의 선형 결합은 Convex Function이다.

증명은 굉장히 간단하기 때문에 굳이 적지 않겠다.

Convex Optimization

다음 최적화 문제를 보자

에서 $f, g_i$가 convex function이고, $h_j(x)=0$의 해집합이 convex set일 때 이를 Convex Optimization이라고 부른다.

Linear Programming

다음 문제를 보자.

이 문제는 라그랑주 승수법(Lagrange multiplier method)를 사용하여 dual problem으로 바꾼 뒤, 원래 문제보다 적은 변수들로 문제를 해결할 수 있다.

더 자세한 설명은 논점을 벗어나므로 해당 방법에 대해 자세히 소개된 포스트를 첨부한다. -> Duality

Example

대신 어떻게 푸는 건지에 대해 간단한 예시를 도식화하여 풀어보자.

이때 조건이 다음을 만족해야 한다고 하자.

이 조건들을 도식해보면 아래 그림의 회색 영역이 된다.

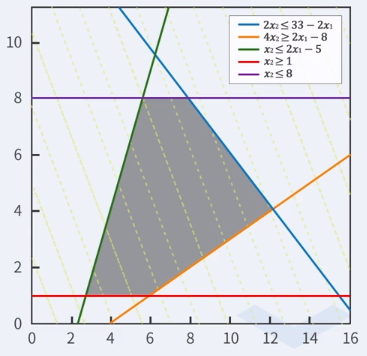
그리고 주어진 식 $\begin{bmatrix} 5 \\ 3 \end{bmatrix}^T\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}$은 위의 노란색 점선들과 같은 기울기로 나타나고, 우리는 여기에서 이 점선이 오른쪽 끝으로 갔을 때에 최소가 된다는 것을 알 수 있다.