2-4. Convex Function

본 글은 K-MOOC의 인공지능 수학 고급(Advanced Mathematics for AI) 강의를 듣고 요약한 글입니다.

Convex set

만약 집합 내의 임의의 두 원소 $x, y ∈ C$ 가 있을 때, 임의의 $0\le \theta \le 1$에 대해 $\theta x + (1-\theta)y ∈ C$를 만족하면 $C$는 Convex set(볼록 집합)이다.

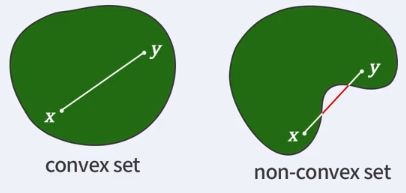
위 그림처럼 임의의 두 점을 잡아 두 점을 연결하면, 해당 선분위의 점들 모두 집합위에 포함된다.

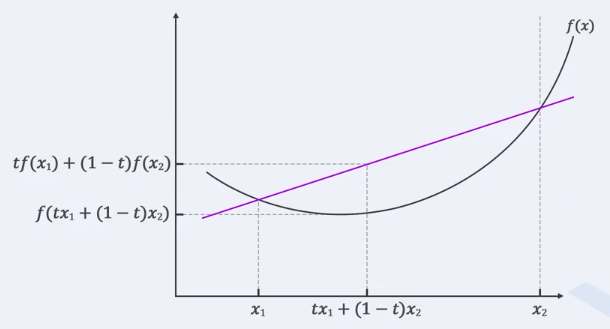
Convex Function

$f$의 정의역(domain)이 Convex set이고, 임의의 두 원소 $x, y$와 임의의 $0\le \theta \le 1$에 대해 다음 식을 항상 만족하면, $f$는 Convex Function(볼록 함수)이다.

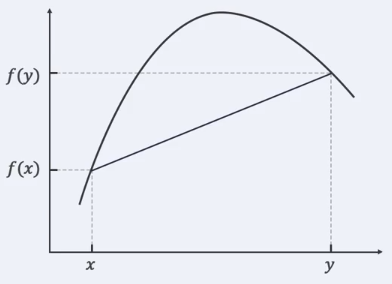
Concave Function

위와 같은 조건에 대해 위 식을 항상 만족하면 $f$는 Concave Function(오목 함수)이다.