3-2. Maximal Margin Classifier

본 글은 K-MOOC의 인공지능 수학 고급(Advanced Mathematics for AI) 강의를 듣고 요약한 글입니다.

Classifier

다음과 같이 Blue / Pink 로 구분된 이차원 상의 점들이 있다.

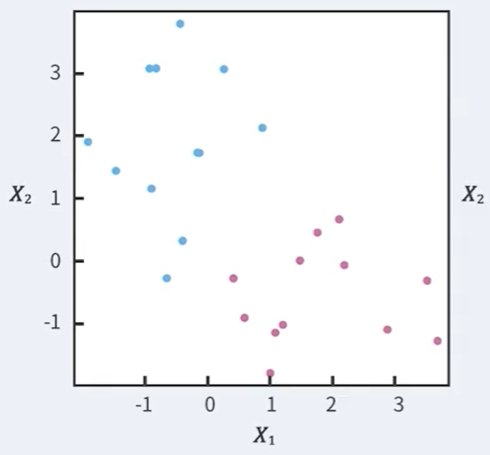
새로운 점이 들어왔을 때 Blue인지, Pink인지 예측하는 문제이다.

이러한 예측을 위해 구분자를 찾아내야 하는 데, 이를 decision boundary라고 하며

다음과 같은 직선 방정식으로 정의해보자.

이때 생기는 문제는 가능한 decision boundary가 너무 많다는 것이다.

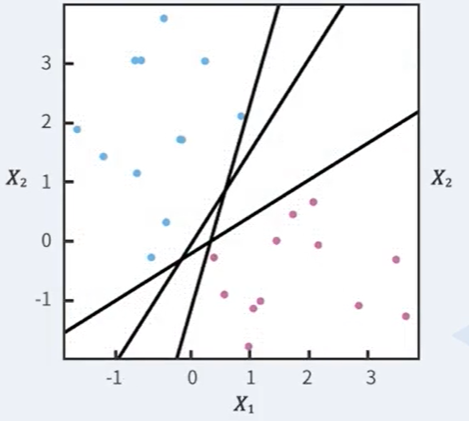
이때 어떤 decision boundary가 적합한 것인지를 찾아내는 문제가 추가로 발생한다.

Idea

다음과 같이 생각해보자.

• boundary에 가장 가까운 점들을 찾아서, 그 점들을 support vector라 이름 붙이자.
  
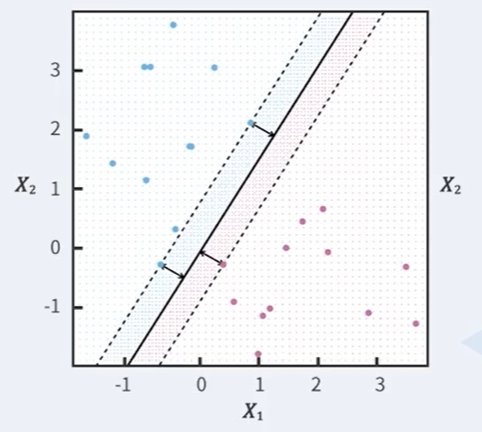
• 그 다음 support vector와 decision boundary 간의 거리를 구해 margin이라 이름붙이자.
• 이때 이 margin을 최대로 하는 decision boundary를 찾자.

Margin

$i$번째 데이터를 $(X_1^{(i)},X_2^{(i)},y^{(i)})$ 라 하자. ($y^{(i)} ∈ {-1, 1}$)

이때, $i$번째 데이터부터 boundary까지의 거리는 다음과 같다.

(단, $\beta_1^2 + \beta_2^2 = 1$)