
본 글은 K-MOOC의 인공지능 수학 고급(Advanced Mathematics for AI) 강의를 듣고 요약한 글입니다.
Maximal Margin Classifier
이 방법은 영역을 정확하게 자르는 것이 불가능 할 수 있다.
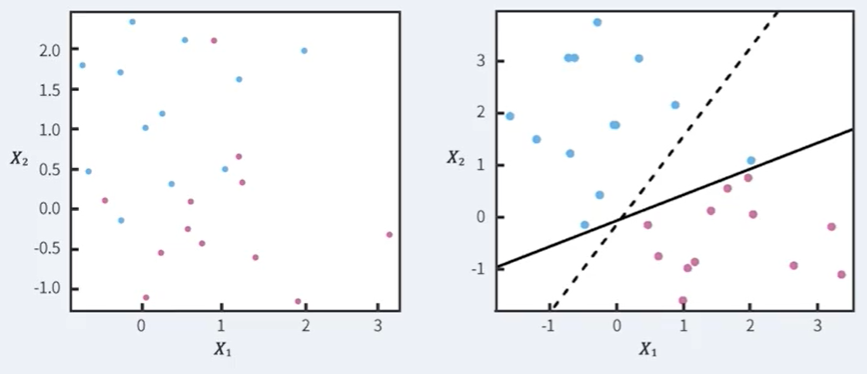
또한 두 번째 그림처럼 Outlier에 굉장히 민감해진다.
Overfitting vs Generalization
기계학습의 목적은 주어진 데이터를 가능한한 정확히 학습하는 것이 아니다.
기계학습의 목적은 새로운 데이터에 대해서 최대한 정확하게 예측하는 것이다.

간단히 예를 들면 위 그림에서 세 번째 그림이 네 번째 그림보다 좀더 잘 설명할 수 있다는 것이다.
Idea
다음 두가지를 허용해보도록 하자.
- margin 안에 데이터가 있어도 괜찮다.
- decision boundary 건너편에 다른 데이터가 있어도 괜찮다.
즉, 에러들에 대해 유연해지자는 의미이다.
Soft Margin Classifier
Soft Margin Classifier 역시 이차계획법으로 정의한다.
Decision boundary가 일 때,
for all data
여기서 는 관대함을 나타내는 변수이다. 즉, 에러들이 C를 넘지 않는다면 상관없다는 것이다.
Penalty parameter
이 를 바로 Penalty parameter라 부르고, 이에 따라 아래와 같이 decision boundary가 바뀐다.
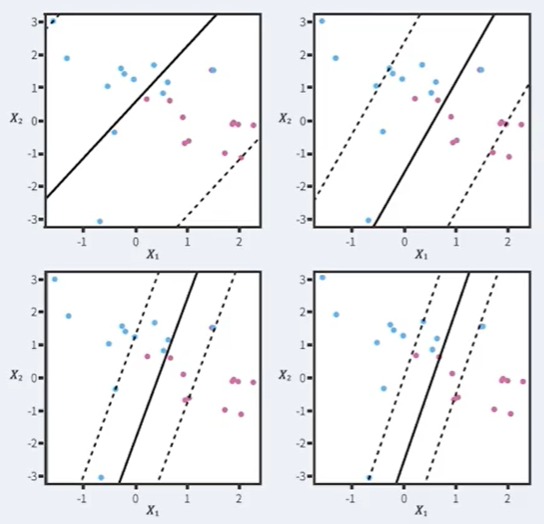

Overfit보다는 General하게..