3-5. Kernels

본 글은 K-MOOC의 인공지능 수학 고급(Advanced Mathematics for AI) 강의를 듣고 요약한 글입니다.

Kernel

Kernel들의 종류를 다시한번 보자.

• Linear Kernel
  $K(X^{(1)},X^{(2)}) = <X^{(1)},X^{(2)}>$
• Quadratic Kernel
  $K(X^{(1)},X^{(2)}) = (<X^{(1)},X^{(2)}>)^2$
• Polynomial Kernel of degree d
  $K(X^{(1)},X^{(2)}) = (<X^{(1)},X^{(2)}>)^d$
• Radial Basis Function(RBF)
  $K(X^{(1)},X^{(2)}) = exp(-\gamma \|X^{(1)}-X^{(2)}\|)$

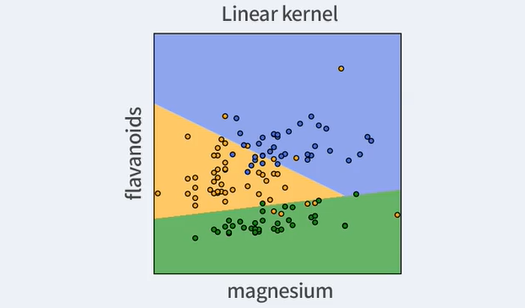
Linear Kernel

이 경우는 사실 커널을 사용하지 않는 것과 별 다를 바 없다.

그냥 선형의 decision boundary를 찾았다는 것이다.

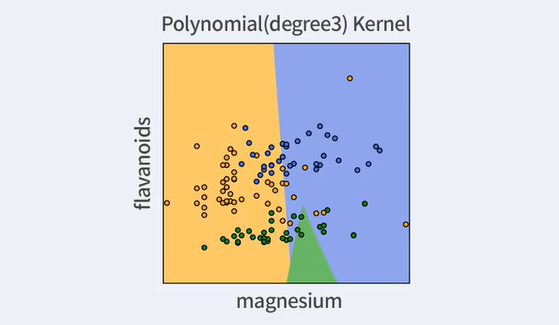
Polynomial Kernel of degree d

이는 데이터의 분포가 다항식의 형태로 전개될 때 유용하다.

하지만 상당히 안좋은 output을 보여주고 있다. 이는 데이터가 polynomial의 형태로 분포하지 않기 때문이다.

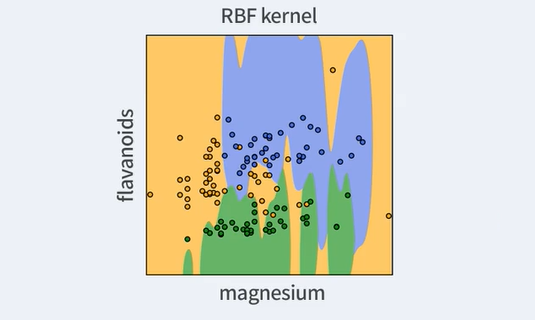
Radial Basis Function(RBF)

RBF는 norm을 사용하는 kernel이다.

이는 두 데이터의 거리에 따라 가까이 있는 것은 뭉치게 되고, 멀리 있는 것은 더 멀리 떨어지게 된다는 것이다.

그렇기 때문에 대부분의 경우 좋은 성능을 보여준다.

• $\|X^{(1)} - X^{(2)}\|$ : 두 점 사이의 거리
• $\gamma$: hyperparameter, $0\le\gamma\le1$

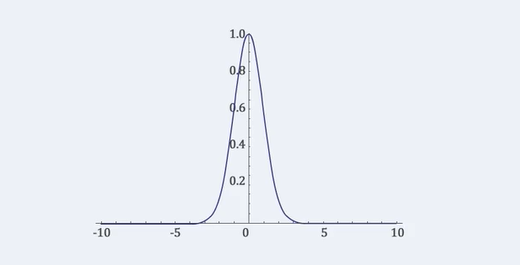
위 그래프에서 볼 수 있듯, 두 데이터 사이의 거리가 가까울 수록 1에 가까워지고, 멀어질 수록 0에 가까워진다.