3-4. Support Vector Machine

본 글은 K-MOOC의 인공지능 수학 고급(Advanced Mathematics for AI) 강의를 듣고 요약한 글입니다.

Soft Margin Classifier

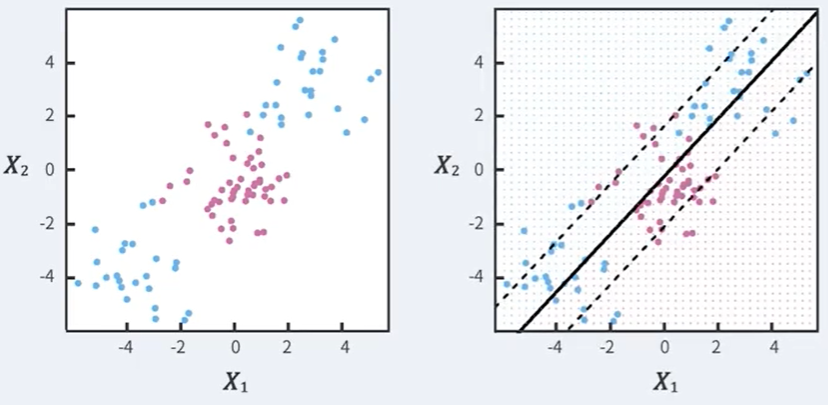
하지만 이 방법 역시 문제가 있다.

만약 점선이 다음과 같이 분포되어있다면 Soft Margin Classifier는 다음과 같은 결과를 내버릴 것이다.

Idea

• 비선형 decision boundary를 찾는다

• 점들의 분포를 바꿔본다.

• 점들을 새로운 공간으로 옮겨서 그들이 linearly하게 분리되도록 해본다.

  

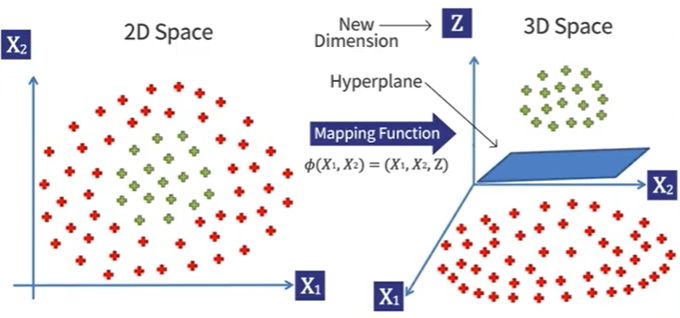
위 세 방법은 사실 다 같은 말을 하고 있으며, 이러한 방법을 바로 kernel method라고 부른다.

Kernel

• $\phi$: mapping function
• $\phi(X_1,X_2) \rarr (Z_1,Z_2,Z_3) \equiv (X_1^2,\sqrt{2}X_1X_2, X_2^2)$
• $K$: kernel function
• $K(X^{(1)},X^{(2)}) \equiv (<X^{(1)},X^{(2)}>)^2 = <\phi(X^{(1)}),\phi(X^{(2)})>$

커널은 이렇게 이차원 데이터를 삼차원으로 바꾸어 준다.

또한 이 외에도 다양한 커널들이 존재한다.

• Linear Kernel
  $K(X^{(1)},X^{(2)}) = <X^{(1)},X^{(2)}>$
• Quadratic Kernel
  $K(X^{(1)},X^{(2)}) = (<X^{(1)},X^{(2)}>)^2$
• Polynomial Kernel of degree d
  $K(X^{(1)},X^{(2)}) = (<X^{(1)},X^{(2)}>)^d$
• Radial Basis Function(RBF)
  $K(X^{(1)},X^{(2)}) = exp(-\gamma \|X^{(1)},X^{(2)}\|)$

Support Vector Machine

지금까지 다룬 이 모든 방법들이 바로 Support Vector Machine이라고 불리는 것들이다.

• Maximal Margin Classifier
• Soft Margin Classifier
• Use appropriate Kernel