본 글은 K-MOOC의 인공지능 수학 고급(Advanced Mathematics for AI) 강의를 듣고 요약한 글입니다.
Example
패스트푸드 체인점이 커피 원두의 종류를 바꾸려고 하고 있다.
새로운 원두의 소비자 선호도를 조사하기 위해서 회사는 무작위로 n=100의 커피 소비자 표본을 만들었다.
컵에는 A와 B로 마킹을 해두었다.
새 원두를 A에, 기존 원두를 B에 넣어 두고, 절반의 시간이 흐른후 A와 B의 순서를 바꿔두었다.
이 때, 두 원두에 대한 선호도 차이를 조사하려고 한다.
Model
- θ: 소비자가 새 원두를 고를 확률
- X1,…,Xn: 베르누이 분포에 의한 무작위 표본 (성공과 실패에 대한 분포이기 때문에 베르누이 분포가 적절하다.)
P(xi∣θ)=θxi(1−θ)1−xiP(xi∣θ)=i∏nθxi(1−θ)1−xi
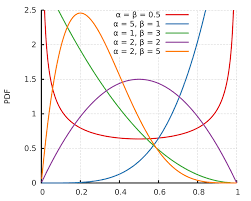
Prior
Beta distribution
이 모양은 베르누이 분포의 모양과 유사하다.
π(θ)=Γ(α)Γ(β)Γ(α+β)θα−1(1−θ)β−1E[θ]=α+βαVar[θ]=(α+β)2(α+β+1)αβ
Posterior
원래 분모도 함께 계산을 해줘야 하지만, 분모는 영향을 주지 않기 때문에 분자만 계산하자.
π(θ∣x)∝p(x∣θ)π(θ)=θi=1∑nxi(1−θ)n−i=1∑nxiΓ(α)Γ(β)Γ(α+β)θα−1(1−θ)β−1∝θ(αi=1∑nxi)−1(1−θ)(β+n−∑i=1nxi)−1
- 이 결과 이 모양이 베타 분포와 비슷하다는 것을 알 수 있다. (Beta(α′,β′))
- α′=α+∑ixi
- β′=β+n−∑ixi
Conjugate Prior
이렇게 Prior과 Posterior가 같은 분포 그룹에 속하게 되면 이때의 Prior를 Conjugate Prior, 켤레사전분포라고 부른다.
대표적인 분포 그룹의 예로 Exponential Family가 있다.
- Normal, Exponential, Gamma, Beta, Bernoulli, Dirichlet, Categorical, Poisson, Geometric
즉 여기에서는 베타분포가 베르누이 모델의 켤레사전분포가 되는 것이다.
- Conjugate Prior는 매우 편리하다.
- 하지만 Conjugate Prior가 있는 모델이 있고 없는 모델이 있다.
- 따라서 Conjugate Prior가 포함되는 모델을 만든다면, 이를 후에 계산할 때 훨씬 간편하다는 장점이 있다.


