본 글은 K-MOOC의 인공지능 수학 고급(Advanced Mathematics for AI) 강의를 듣고 요약한 글입니다.
Bayesian Network
Bayesian Network는 DAG(유향 비순환 그래프)로서, 각각의 노드가 그 부모에 대한 조건부 확률을 갖는다는 특징이 있다.
그리고 각 노드들의 Joint Probability는 다음과 같이 조건부확률의 곱으로 나다난다.
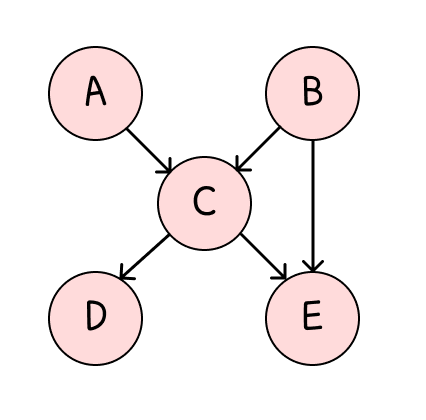
P(A,B,C,D,E)=P(A)P(B)P(C∣A,B)P(D∣C)P(E∣B,C)
Example
- 샐리의 집에 침입 알람(A)이 울렸다.
- 그녀의 집에 도둑(B)이 든 것일까 아니면 지진(E)이 난 것일까?
- 그녀는 차 라디오(R)를 틀어 지진뉴스가 있는지 확인했다.
이때 각 확률들의 Joint Probability를 다음과 같이 구할 수 있다.
P(A,R,E,B)=P(A∣R,E,B)P(R∣E,B)P(E∣B)P(B)
자 여기에서 다음과 같은 가정을 추가해보자.
- 알람은 라디오에서 지진 뉴스가 있다고 해서 울리지는 않는다.
- 라디오 방송은 도둑이 든 것과 직접적인 관련은 없다.
- 또한 도둑과 지진은 직접적인 관련이 없다.
이때, 위 조건들은 독립성을 나타내므로 다음과 같이 Joint Probability를 나타낼 수 있다.
P(A,R,E,B)=P(A∣E,B)P(R∣E)P(E)P(B)
그리고, 이를 베이지안 네트워크로 나타내면 다음 그림과 같다.
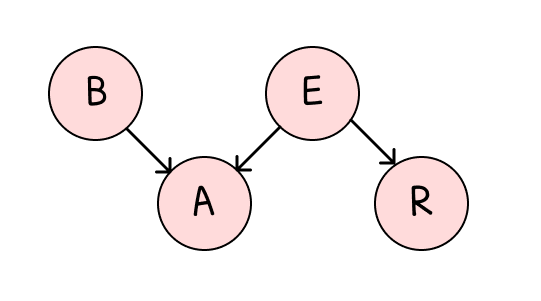
그리고 각 확률을 다음의 테이블로 나타내면 다음과 같다.
-
p(A∣B,E)
| Alarm=1 | Burglar | Earthquake |
|---|
| 0.9999 | 1 | 1 |
| 0.99 | 1 | 0 |
| 0.99 | 0 | 1 |
| 0.0001 | 0 | 0 |
-
p(R∣E)
자 이제 처음으로 돌아가자.
-
Initial evidence: 침입 알람이 울렸다.
이때 도둑이 들었을 조건부 확률은 다음과 같다.
p(B=1∣A=1)=∑B,E,Rp(B,E,A=1,R)∑E,Rp(B=1,E,A=1,R)=∑B,E,Rp(A=1∣B,E)p(B)p(E)p(R∣E)∑E,Rp(A=1∣R=1,E)p(B=1)p(E)p(R∣E)≈0.99
-
Additional Evidence: 하지만 지진이 났다는 뉴스가 라디오 방송으로 나왔다면
p(B=1∣A=1,R=1)≈0.01
로 도둑이 들었을 확률이 급격히 낮아진다.



