4-5. Independence in Bayesian Networks

본 글은 K-MOOC의 인공지능 수학 고급(Advanced Mathematics for AI) 강의를 듣고 요약한 글입니다.

Independence in Bayesian Networks

3개의 노드와 두개의 링크를 가진 모든 Bayesian network는 다음과 같이 구분할 수 있다.

$A \perp\!\!\!\!\perp B|C$ : (a), (b), (c)

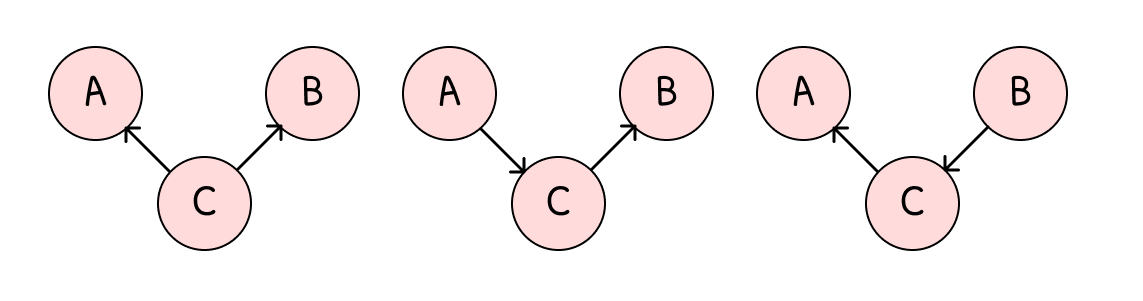
$A \,\,\cancel{\perp\!\!\!\!\perp}\,\, B|C$ : (d)

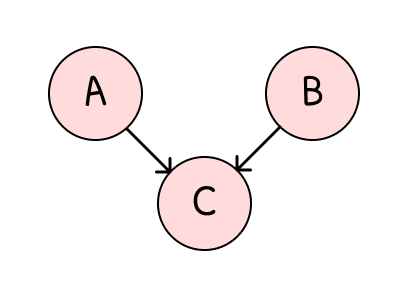
왜 위와 같이 되는지 알아보자.

(a)

(b)

(c)

(d)

따라서 (a), (b), (c) 의 경우 독립이고, (d)는 독립이 아닌 것이다.

C를 배제한 A와 B만의 독립 여부

만약 C가 주어지지 않았을 경우 어떨까?

$A \,\,\cancel{\perp\!\!\!\!\perp}\,\, B$ : (a), (b), (c)

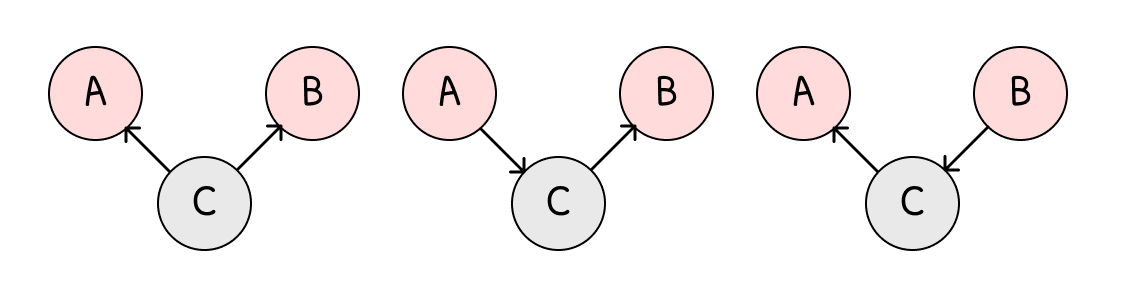
$A \perp\!\!\!\!\perp B$ : (d)

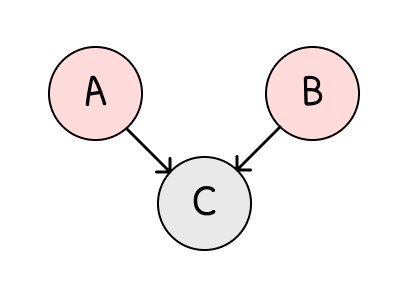
이때는 위처럼 반대로 (d)의 경우만 독립이다.

Collider

$C$가 두 개 이상의 incoming link가 존재하고, $A \perp\!\!\!\!\perp B$ 이며 $A \,\,\cancel{\perp\!\!\!\!\perp}\,\, B|C$를 만족할 때, C를 collider라고 부른다.

만약 반대로 $C$가 최대 한 개의 incoming link가 존재하고, $A \perp\!\!\!\!\perp B|C$이며 $A \,\,\cancel{\perp\!\!\!\!\perp}\,\, B$를 만족할 때, C를 non-collider라고 부른다.

General Rule for Independence

$(X,Y,C)$가 주어지고, $X$에서 $Y$로 가는 모든 경로가 $C$에 의하여 막혔을 때, $X$와 $Y$는 $C$에 대한 조건부 독립이라고 부른다.

위에서 path $P$가 $C$에 의해 막혔다는 것은 다음 중 하나를 만족함을 의미한다.

• path $P$에 collider가 존재할 때, 해당 collider 혹은 그 자손들이 C에 없는 경우.
• path $P$의 non-collider가 C에 있는 경우

Example

Is $a \perp\!\!\!\!\perp e | b$ ?

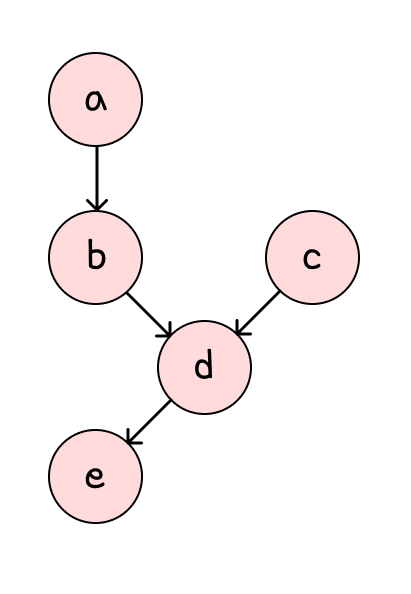
$a-b-d-e$ 경로에서 $b$가 non-collider이므로 $b$에 의해 모든 경로가 막혀있다.

즉, 독립이다.